解析力学：見かけの力

今回は,異なる座標を採用している人から見たときに,物体の運動がどのように表されるかを調べる事にしよう.とは言っても,極座標のような面倒なものにはまだチャレンジしない.それは第 2 部でごく簡単に紹介するつもりでいる.ここではそのための基本を学ぶために簡単な例だけを示すのである.

その前に少し聞いておいて欲しいことがある.力学のページでは,まず,直線的に運動する物体について考察して,ニュートンの運動方程式を理解したのだった.そして同じ事が,,の 3 成分に対してそれぞれ独立に成り立つものだと信じて,次のような 3 つの式を用意したのだった. このことは「我々の日常の範囲では十分に成り立っている」ことが確かめられているので,ただ闇雲に信じているだけの状態とは少し違っているわけだが.

さて,このような 3 つの式を立てたとき,あまり意識していないかも知れないが,デカルト座標をごく自然なものとして受け入れ,採用したことになる.3 つの軸の指す方向をそれぞれ独立した対等なものだと考えているからである.これら 3 つの式をベクトルを使ってまとめて表すと, のように書けるが,この有名でシンプルな形は,デカルト座標系で成り立っている方程式だと言えよう.この形の運動方程式が唯一絶対的なものだと考えてはいけない.別の座標系を採用した場合には,この方程式は別の形式で書き直されることになるのである.

例えば,ある点の周りを綺麗に円運動する物体について論じる時には,むしろ極座標を使った式に書き換えた方が便利なことがある.普通の真面目な力学の教科書には,そういう場合のテクニックが色々と説明されているわけだ.しかし私は計算技術的なことには興味がないので,その辺りの話にはあまり踏み込まないでいるのである.

慣性系

等速運動する列車の中の人が物体の運動を論じるとどうなるだろう？窓の外に見える景色は次々と後へ飛び去って行くが,列車の中は平穏無事だ.車内のどこか,自分のごく近くにある物体の位置ついては,動いている列車のどこかを基準にして論じ,外の世界との関係はあまり考えないことだろう.

列車が方向に速度で進んでいるとすると,外の世界の座標 (x,y,z) と,車内の人の使う座標 (x',y',z') との間に, という関係があることになる.ただし簡単にするために t=0 の瞬間には両者が基準にしているものが同じ位置にあったと仮定している.秒後には列車はだけ先へ進んでいるから,外の世界の人がだと言っている点は,車内の人にとってはだけ後方に見えるという意味である.

さて,物体の運動は (1) 式で表せるとのことだったが,これを (x',y',z') を使って書き換えたらどうなるだろう.手続きは簡単だ.(2) 式を (1) 式に代入してやればいい.やについては何も変わらないのはすぐ分かる.については, x=x'+vt と書き換えて代入してやればいいのであり,難しくもない.

このの項をで一回微分しただけではが残るが,もう一度微分する必要があるので結局はきれいに消えてしまうだろう.よって,列車内で成り立つ運動方程式は, という,外の世界と全く同じ形となっている事が分かる.実際,列車が安定して静かに走っている時には,我々は車内の物体の動きについて何らの違和感も感じない.ボールを真上に投げ上げても,ボールが列車の後方へと飛び去る事はない.普通に地面に立っている時と同じ法則が成り立っているのである.

「慣性系」という名前の由来はこれだ.慣性運動しているものを基準にした座標系のことである.それがどんな速度であろうとも,慣性系においては,どれも同じニュートン力学が成り立つのである.

それが成り立たなくなるのは,列車が加速や減速を掛けた時,あるいは,列車が左右に揺れたりする場合だ.吊り革は勝手に揺れ,立っている乗客は前のめりに倒れたりする.次にその状況について計算してみよう.

加速度系

列車が加速する場合を考える.計算し易いように加速度は一定だとしよう.そのとき, という座標変換を使えばいい.速度を $v_{0}$ と書いたのは,今回,列車の速度は刻々と変化するからだ. $v_{0}$ は t=0 の時点での列車の速度を表している.この式の理屈は前と同じで,秒後に列車は $v_{0}t+ 1/2 at^2$ だけ前に進んでいるから,という意味である.

(3) 式の一番初めの式を $x=x'+v_{0}t+ 1/2 at^2$ と書き直して (1) 式に代入してみよう.第 2 項は先ほどと同じであるから消える.しかし第 3 項はで一回だけ微分するととなり,もう一度微分するとが残る.つまりこの場合,運動方程式の成分だけは, のように僅かな変更を受けるということである.これは何を意味していると解釈できるだろうか.少し移項してやろう. つまり車内の物体には,列車の加速度とは反対の方向に,だけの力が余分に掛かっているように「見える」という意味である.たとえ F_x =0 であったとしても物体はこの力によって勝手に加速することになる.このとき本当は誰も押してなんかいない.作用反作用の法則を満たさないこの力を「見かけの力」と呼ぶ.

列車が加速している時に後方に向かって力を受けるのも,急ブレーキによって前のめりになるのも,吊り革が揺れるのも,すべてこの見かけの力で説明が付く.座っている客がシートに押し付けられるのもそうだ.加速中にボールを真上に投げ上げれば,ボールは後へ行くだろう.

しかし本当は,列車が加速した時に,物体が列車の動きに付いて来れてないので,相対的に位置に差が出るだけの話に過ぎないのである.その物体を列車の動きに付いて来れるように引っ張ってやるためには力が要るので,あたかも物体に力が掛かっているように思えるのである.

さあ,これで「座標変換により力が生じる」ということの基本を説明し終えたわけだが,SF と区別が付いただろうか.

そうがっかりしないで欲しい.一般相対性理論ではこの考えが基本にあって,そこから「重力さえも見かけの力の一種に過ぎない」という話になり,SF のような話へと発展して行くことになるのであるから.

力の座標変換

ところで今回の座標変換の手続きがあまりにも簡単すぎて,拍子抜けしてしまった人がいるのではないだろうか.「いや,こんな簡単に済ませては正しくないのでは」と疑う人もいるだろう.例えば気になるのは,力 F_x , F_y , F_z については何の変換もしなかったが,本当にそれでいいのかという点だ.こういう部分は強く疑って欲しい.

これは数学だけでは片付かない問題だ.果たして力は,動いている人から見た場合と止まっている人が見た場合とで同じだろうか.同じだと信じられる根拠はある.動いていても止まっていても,重力は同じように働くから,とか,駅のホームで殴り合いの喧嘩をしているのを通過電車の窓から見ても,ダメージは変わらないように見える,とか.まぁ,納得が行くまで色々考えてみて欲しい.

しかし,使っている座標軸の向きが互いに異なる場合には確かに変換が必要だ.ある人が「力が私の右手方向に向かって掛かっている」と観測する時,その人に対して真右の方を向いている別の人が見たら,その力は私の正面方向に向かって働いていると見えることになるだろう.そのような変換は今回は必要がなかったのでしなかっただけのことだ.次回の話では必要になるだろう.

こんな風に,場合によって変換したりしなかったりするのではなく,どんな場合にでも当てはめられるような形式的な手続きはないだろうか？こういうことを考える人のためには,座標の「基底ベクトル」なんて話を持ち出せばいいのだが,私はこの段階から必要以上に議論を高度化したくないので説明しない.いや,そんなに複雑な話ではなく,変換前後の座標軸の内積を計算して使えばいいという話であって,要は,力のベクトルは座標に沿って測られる量だということである.こういう話が好きな人は自分で調べて活用してもらったらいいと思う.

形式を整えておけば,どんな場面に対しても深く考えることなく一定の手続きを当てはめる事が出来るという利点があり,複雑な議論に突入した時には大変助かるものだ.

相対性原理

今回の話の前の方で,慣性系であれば速度の如何を問わず,同じようにニュートン力学が成り立つのだと話した.これはつまり,列車の窓を閉じていれば,自分が動いているのか止まっているのか,車内にある物体の力学現象を観察した限りでは判別できないということだ.

このことを「ガリレイの相対性原理」と呼ぶ.また (2) 式の変換を「ガリレイ変換」と呼ぶ.ガリレイはニュートンが生まれる直前に没しているので,ニュートン力学と絡めた説明の仕方は後世のものである.しかしガリレイはニュートン以前にこのことに気付いていたので,彼に栄誉を帰してそのように呼ぶわけだ.

さて,列車の窓を開けて外を見てもいいだろう.本当は自分の乗っている列車の方が完全に止まっていて,空気や地面や建物が一斉にこちらに向かって移動して来ているのかも知れないではないか.そういう考え方は何もアインシュタインの相対性理論から始まったわけではないのだ.

念のため言っておくが,科学者は本気で「止まっているのは列車の方かも知れない」などと疑っているわけではない.列車が速度を上げるときには,車内には見かけの力が働くだろう.そのことをもってして,実際に動いたのは自分の方なのだと知ることが出来るからだ.しかし,ひとたび慣性系になってしまえば,本当はどちらが動いているかなんてものは意味がないということだ.ニュートン力学でさえも,絶対的な静止座標の存在というものを前提としていないのだ.

4 次元的世界観

ガリレイ変換は慣性系から慣性系への座標変換だという意味がある.この式には時間が含まれているだろう.そこで,ちょっと面白い考え方をお見せしよう.

我々は時間を横軸に,位置を縦軸にして物体の運動をグラフにすることが出来る.次のような具合だ.

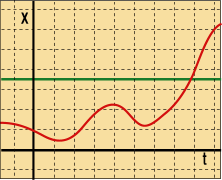
赤色は加速減速を繰り返している物体を表し,緑色は同じ位置でずっと停止している物体を表している.これらの物体の運動を別の慣性系から見たら,どう見えるだろうか.この同じグラフの上に重ねて,軸を描いてやることにしよう.ガリレイ変換を使えばいい.

いや,本当に書き直すべきは軸ではないのだ.

そもそも軸,軸とは何かと言えば,それぞれ, x=0 , t=0 であるような直線のことである.すると,軸としては, t'=0 となるような直線を引くべきであろう.ここで出してきたというのは,動いている人が感じる時間のことである.しかし,時刻というのは動いている人も止まっている人も共通のものを使っているので,結局は t=0 となる直線を引けばいいことになる.

・・・いや,動いている相手と自分とで同じ時間を使っても良いかどうかは良く考えてみないといけない問題であって,本当は軽々しく受け入れてはいけないのだ.相対性理論というのは,そこを良く考えた結果として生まれたのであった.しかし昔は誰もそんなことを疑いはしなかったので,ここは同じように何も考えないで受け入れてやろうではないか.相対論をまだ学んでいない読者にとってはそうする方が常識に合うであろう.つまり,軸は前と同じでいいことになる.

同じように,軸について考えてやろう.これは x'=0 となるような直線を引くべきであり,(2) 式に当てはめてやると, x=vt である.つまり,軸をグラフの上に重ねて描く場合には,斜めを向いた直線として表してやるべきだと言える.

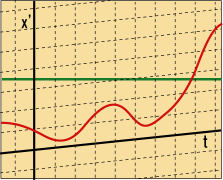
このグラフは正しいだろうか？例えば緑色の線は,系から見れば,徐々にのマイナスの方へ移動しているように見えるだろう.どうやらこれで合っているようだ.

さあ,どうだ！？自分はデカルト座標しか使うつもりはないと心に決めていた読者も,知らない間に斜交座標と同じ理屈を使っていたことになるではないか.

3 次元空間に時間軸を追加すれば 4 次元になる.4 次元のグラフ上に物体の運動が表されており,同じグラフ上に別の斜交座標を引き直してやれば,それぞれの点は幾つであると読み換えてやればいいことになるのか・・・.ガリレイ変換というものをそのような完全に幾何学的な意味で捉えることも出来る.

4 次元から 4 次元への座標変換という幾何学的考えは,何もアインシュタインの相対性理論の専売特許というわけではないのである.