作用
前回出てきた母関数について,その利用法を色々と話したい.いや,実用的なものではなくて,理論体系の視野を広げるというものだが.
そのために,この関数に何か特別な名前が付いていてくれると助かるのだが,残念ながらあまり良い呼び名はないようだ.その呼び名はこの少し後で出てくる.いや,なんかすでに出ているような気もするのだが,まだ内緒だ.
この関数には時間は含まれていないが,中に含まれる
は時間によって変化する.よって,
を時間で微分してやることには意味があり,次のように表せる.
この中にある
は
に等しい.疑う人は,前の記事の (7) 式でその関係が出てきているので確かめて欲しい.よって,
であり,これを積分すると,
となる.本来は任意の積分定数を加えるところだが,前回までと同様,理論に影響が無いのでわざと省いてある.
これは何を意味しているだろうか.運動の進路に沿って運動量を積分して作る謎の量.このように表されたを「作用」と呼ぶ.作用と言えば,あの,ラグランジアン
を時間積分した「作用
」を思い出すだろう.紛らわしいと思うかも知れないが,手違いで全く異なる概念に同じ名前が付いてしまっているというのではない.実は同じものなのである.なぜなら,作用
は,
と変形でき,第 1 項は
そのものである.エネルギーが保存されるような単純な系ではハミルトニアン
が一定値であるため,
である.歴史的には
の方が先に「作用」と呼ばれており,最小作用の原理とは元々は
のことだったらしい.力学の理論が試行錯誤しながら発展してきたことがうかがえる.
相空間上の面積
この (1) 式で表された作用という量だが,これを周期的運動に当てはめると面白い.
まず,相空間という抽象的な空間を想像してみる.これは多数の運動量と多数の位置座標
を共にデカルト座標の座標成分のように考えて作る多次元空間である.質点が 1 次元に制限されて動く場合を考える時だけはその運動量成分と合わせても 2 次元にしかならないので紙の上に描くことができる.
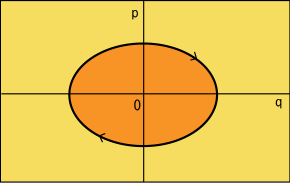
ここに描いたのは,バネによって一方向に振動する質点の運動の軌跡を相空間上に表した図である.横軸が位置を表しており,縦軸が運動量を表している.運動量が正の時には位置が正の方向へ進むのだから右回りになるわけだ.このように,周期運動というのは相空間内の閉じた曲線として表される.
(1) 式で表される作用というのは,この図の場合,この曲線が囲んでいる領域の面積を表している.もし成分がもっと増えた場合には,
と
の組が作る 2 次元平面をそれぞれ別々に考えれば,それぞれの上に輪が描かれるわけだが,
はそれらの多数の輪の面積の合計になっている.
面白いことに,位置や運動量を正準変換によって別の変数,
で表すことになったとしても,この面積の大きさ,つまり,この作用
の値は変わらないのである.座標を自由に選んでも値が変わらないということは,それはエネルギーなどと同じように,物理的に重要な意味を持っている量だとは言えないだろうか.
いや,ちょっと待てよ.確かに面白そうな話だが,そんなはずはないだろう.前回までの話で,や
を定数にするための正準変換を求める話をしていたはずだ.
や
が定数になってしまったら,それは相空間上で常に静止しているのだから,
の値は 0 になってしまうのではないだろうか.
その通り,この話には少し条件があるのだ.それは正準変換の母関数が時間を含まないことである.その条件の下でなら今の話が成り立っているということを今から説明しよう.
積分不変量
今,正準変換の母関数がという形であり,時間
をあらわに含んでいないとしよう.この全微分を計算すると
となるが,この偏微分の部分は正準変換の公式を適用すれば,
と書き換えられる.これを運動の始点から終点まで積分すると,左辺は
となるが,周期運動では始点と終点が同一であるため,0 となる.よって,(2) 式の右辺も同じように積分してやれば,
が言えるわけである.
この説明を見る限りでは母関数としてというタイプのものを使って変換をしたときにしか成り立っていないように思われるかも知れないが,そうではない.
以外のタイプの母関数を使って変換をしたとしよう.その後では旧変数と新変数の関係が導かれているのだから,それを使って母関数のタイプを
に書き換えてやることが出来るだろう.それを使っても結局同じ変換が実現できるわけだ.
だから母関数が時間をあらわに含んでいない限り,この話はどのタイプの母関数を使っても成り立っていることになる.
Sを使った変換
ここまでの話では,作用と呼ばれる謎の不変量と関数とがたまたま等しくなっていたという感じでしかない.母関数としての
に注目するのはこれからだ.
前回の話の結論を思い出そう.このを母関数として使った場合,新運動量
は一定値
となり,新座標
は
となるのだった.
これを相空間に図示すると,次のような状況になるだろう.
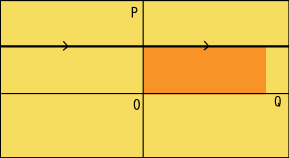
これは周期運動に適用した場合であってもこのように変換される.いつまで経っても元の場所には戻って来ないので周期運動っぽくはないのだが,別に矛盾があるわけではない.これは回転運動を角度で表しているようなものである.角度
は一周して
になったとしてもさらに回転を続け,
,
と増え続けて,元の値には戻って来ない.これと同じようなものである.
新座標にどんな意味を持たせるかは場合に応じて自由であるが,周期運動に適用した場合のように,角度の意味を持たせてやりたい場合にはこれを「角変数」と呼び,
という記号で表すことがある.その場合,定数
には角速度の意味合いがあるわけだ.それを見越して最初からこの記号を当てておいたのである.すると
というのは初期位相といったところか.
ところで,今,変換の母関数としてを使っていて,これには時間が含まれていないのだから,先ほどの不変量の話が成り立つ.上の図は閉曲線を描いているわけではないが,運動が一周期巡ったところで切った長方形の面積がそれにあたる.このことを利用して,一定値である
の値を決めてやることはできないだろうか.いや,残念ながら,次のような関係が言えるだけだろう.
一次元に限った周期運動を考えるならば,もう少しすっきりした,次のような関係になっているとは言える.
新座標
を角度だと解釈した場合には,新運動量
というのは作用と同じ次元の量になっていて,何か深い意味がありそうだということになる.それで,角変数
と対を成す新運動量
のことを「作用変数」と呼び
という記号を当てることがある.一定値なのに変数と呼ぶのもちょっと変ではあるが,これは角変数と正準共役な変数だからということだろう.
作用の意味
では,この作用という謎の量,すなわち相空間に描かれる面積には,物理的にどんな重要な意味が隠されているのだろう?位置と運動量の積なのだから,それは角運動量と同じ次元を持った量であろうことは分かる.実は,ここまで引っ張っておいて非常に申し訳ないのだが,別に大した意味はないし,決まった意味もないのである.
円運動に適用した場合には,これはまさに角運動量を意味しており,今回の,作用量が保存する話は角運動量保存が現れているだけなのである.
バネなどの単振動に適用した場合には,その振動はのような形で書かれると思うが,この場合の作用量
は,エネルギー
をその一定値
で割った量になる.これは後で実例を示そう.確かにその次元は「エネルギー×時間」であり,角運動量と同じになっているが,この場合,作用量の保存は,実質,エネルギー保存則が現れているだけのことである.
前期量子論では,この作用量を使って何事かが恭しく語られているので,ここに何かもっとすごい話が隠されているのかと期待してしまった.私もちょっとがっかりだ.










