今回はごく初歩のニュートン力学の方法によって,波の式を導いてみよう.解析力学の手法は使わないことにする.いきなり解析力学の手法を紹介してしまうと,「波の式というのは解析力学のテクニックを使わないと簡単には求められないものなんだ」なんていう誤った印象を持たれてしまうかも知れないからだ.
さて,何を例に取ろうか.複雑な例を考えるのは面倒くさい.ここでは波の一例を示せればいいのであって,ピンと張ったひもの上にできる波について考える事にする.
ひもと言っても材質は糸だけとは限らない.ギターの弦やピアノ線を想像してもらえば分かるが,金属やナイロンや,動物の腸や毛など,色々ある.これらの楽器の弦は両側から引っ張って,張力を掛けてある.その張り具合によって音程を調整するのである.なぜ張力の掛け方によって音程が変わるのかも,今回の話で説明できるだろう.
モデルの準備
ニュートン力学を使うためには,ニュートンの運動方程式を適用できるようにしないといけない.そのために,ひもの各部分をバラバラに分けて,それらの一つ一つが運動方程式に従う物体であると考えることにする.次の図のようなモデルである.
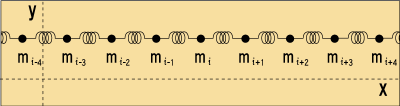
質量を持った幾つもの物体がバネでつながれて並んでいる.この鎖状の構造体は左右から張力
で引っ張られているとする.ひもの材質が何であれ分子,原子が結合して出来ているのだから,ミクロに見ればこんな感じだろう.バネはそれぞれの部分を結合している原子間,分子間の力を譬えているのである.本当はもっと複雑な構造なのだろうけれど,まずは思い切り単純化して考えてやるのが良く使われる手である.このモデルでうまく説明できなければ別のモデルを考えるまでだ.
次に,この中の質点の一つだけを上か下に少しだけ移動させてやったら,何が起こるだろうかというのを想像してみる.次の図のような状況である.
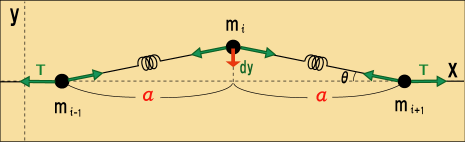
物体間の距離がであり,物体が上に
だけ移動したとする.バネは少しだけ伸びた分,先ほどより強い力で物体を引っ張るだろう.しかし
が
に比べて極めて小さい場合に限定して考えれば,その力は
とほとんど変わらないと見ていい.その
の変化の度合いが無視できる程度だということは計算して示すことも出来るのだが,面倒な割にあまり利益は無いのでここでは省略しよう.
物体は左右から斜めに引っ張られている.その合力の軸成分は打ち消されるが,
軸方向には助け合うことになって,その力は
である.ここで
の時には
と近似できるので,
方向へ働く力は
であると言える.
このような近似の繰り返しによって計算結果が不正確になってしまうのではないかという疑念を持つかも知れない.今から導かれる結果がもし現実離れしていたら,この辺りの誤差の扱いが大雑把過ぎるのではないかという可能性も検討すべきだろう.実際に振幅が非常に激しい場合には「非線形振動」なんていう高校物理ではやらないような現象が出てくる.しかし今は,高校物理でも扱うような波ががひもの上に生じることを導こうとしているのであり,そのためにはこの程度の扱いで十分であることが今に分かるだろう.
さて,上ではたった一つの質点のみが方向へ変位した場合を考えたが,実際は,全ての質点がそれぞれバラバラに動くのである.その場合には右からと左からの力が等しいということはないから,右からの力と左からの力を別々のものとして考えてやらないといけない.しかし
軸方向へ引っ張る力についてはほぼ
ということで釣り合っていると考えておこう.現実には
軸方向への振動もわずかに生じることになるのだろうが,そこが気になって仕方がないという人はレベルアップのチャンスなので,誤差の程度を自分で計算してみて,それが結果に与える影響がどれくらいになるか,あれこれ考えてみるといいと思う.
とにかく,自分と隣の質点との方向の変位の差に比例した力が復元力として効いてくるのであるから,各質点
の運動方程式は次のような形で表されることになる.
まぁ,こんな式が質点の数だけ連立されるわけだ.質点の数が多い場合には解こうとする気力も失せてしまうわけだが,力学の専門書などには線形代数などを使って効率的に解くテクニックが詳しく解説されている.しかし今回はこのような多数の質点についての問題を解く事は目的ではなく,ひもの動きを考えたいのであった.
自由度を無限大へ
ひもの見た目はつぶつぶの質点の集まりではなく,滑らかにつながった連続体である.上で考えたモデルを改造して質点の数を無限に増やして密に敷き詰めれば,そのような連続的な「ひも」のイメージに近いものが出来上がることになる.その変位はという連続的な関数で表されるだろう.つまりこの関数
はひもの形を意味している.
ある一定の範囲を考えて,その中に個の質点があるとする.その幅を
で表すと
という関係があるだろう.これを保ちながら
に近付けるのである.これによって
は無限に狭まるだろう.
しかしこれだけでは質量の合計が無限に増えて困るので,現実と合わせるために次のように考えてやる.つまり,長さ内にある質点の質量の合計を
という値で固定してやる.すると質点 1 個あたりの質量は
だということだ.ここまでの考えを先ほど作った式に代入してやると,
となる.ここからの変形が面白い.右辺の
を無限に 0 に近付けたら,微分の定義式と同じになる部分がある.右辺を分かり易く書き直してみよう.
本当は
記号を付けないと正しくはないが,まだ説明の途中だということで見逃して欲しい.この計算で微分が二つ出来上がる.後の方は微分の定義式と同じ形になっているが,最初の方は見慣れた定義式とは少し違っていて少々困るかも知れない.しかし意味を考えれば
地点での微分を計算した事に相当するのでそのように変形した.
さて,この結果を見てさらに気付くのは,変数が微小変化した時の,関数
の差の形になっているということだ.この全体を
で割って,
を無限に 0 に近付けてやれば,これも微分の定義と同じ形式である.つまり,2 階微分を計算した事に相当するだろう.よって次のように変形.
なお,最後の行は,
が無限に小さいのなら
と見なしても間違いじゃないだろうという甘い考えによって変形してある.こういう格好良くない変形を読者の目に触れさせたくなければ,初めから,
なので……とだけ書いて軽くごまかしてやればいい.それが出来ないのが私の性格だ.
これを左辺の部分と一緒にしてやろう.関数は時間によっても変化するので,実は
ではなく,
という形の関数なのだった.式に書くのが面倒だから今まで黙っていたのだ.この変数の
は位置を表すだけのものであって,時間に依存するようなものではないので,左辺にある時間微分はそのまま偏微分に書き替えてやっても同じ事である.右辺の 2 階微分についても,
は多変数関数なのだから,偏微分で書き表しておかないといけない.また,
はひもの「線密度」を意味するから,これを
として表してやろう.
さあ,出来た!この式は電磁気学のページにも出てきた「波動方程式」と同じ形である.この式の性質については電磁気学のページで話したので詳しくは繰り返さないが,あらゆる形の波がその形を保ったまま,この糸の上を右に左にと移動することが許されるのである.そしてその波形の移動速度
は
という式で決まるのであった.要領の悪い受験生がするように,これを公式として丸暗記する必要などない.ピンと引っ張られているほど変位が素早く回復すること,ひもの材質が重いと動きが鈍くなること,波の動きもその動きに合わせて速かったり遅かったりすること,そういうイメージさえ持っていれば,いつでも思い出せる.
弦楽器の仕組み
さあ,ここまで話したことで,先へ進むための準備はもう整った事になるのだが,ついでだから,一つの話としてまとまりの良いところまで続けよう.
ギターの弦やピアノ線の場合には両端を固定して使うので,
という境界条件を入れて先ほどの波動方程式を解くことになる.すると,この弦の上に乗ることの出来る波形はかなり制限されて,次の図のようなものだけになる.

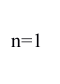

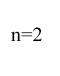



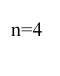

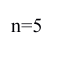

これらのどれか一つだけが許されるのではなく,これらを好きな割合で組み合わせた複雑な波形が弦の上に乗ることを許されるのである.微分方程式を解く過程は省略するが,これらの結果を式で表してやると,
ただし
となる.
は整数である.単に計算の話なので自力で調べてやってみて欲しい.この式の中にある
は周波数を表しており,楽器の場合で言えば,それは音の高さだ.
の場合が最も低い音であり,「基音」と呼ばれる.n が 2 以上の音を「倍音」と呼び,これらのブレンドの具合によって波の波形が決まり,その違いが人間の耳には「音色」の違いとして感じられるのである.
音の高さが「弦の張り具合」と「弦の線密度」と「固定端の位置」によって決まることは経験的に知っていることだとは思うが,そのことが,このように数式によってもバッチリ導かれるわけだ.
この世に無限はあるか
もう少しだけ話を続けたくなった.上に出てきた式の中に整数が使われているが,この
に上限はあるだろうか.理論上はない.しかし現実にはある.
波の式を作るために,質点の数は無限大だという理想を考えたのだった.しかし現実には物質は原子や分子で出来ているのだから,これらが互い違いに上,下,上,下と並んで振動するところが事実上の上限であろう.これ以上波長の短い波は作れない.さらに言えば,に比べて
が非常に小さいという仮定も使っているので,あまり
の小さくなるところまで考えると,その前にボロが出始める.
が大きいということは周波数が高いことも意味している.これは上下振動の速度が速いということでもある.そうなると,ここまでの議論で完全に無視していた空気抵抗の影響もひどく大きいものとなってくるだろう.
自然界には無限大というものは現れないように思える.理論に含まれる数値が無限大になるような状態を実現させようとしてそこを目指して行くと,それまで考えもしなかった別の現象が姿を現し,いつまでも理論の予言の通りに振舞い続けることを拒否するようになる.自然は無限大の存在を嫌うようだ.いや,本当にそうだろうか?










