必要だから説明するのだ
交流と聞くと,家庭用コンセントに来ている 100 V 電源を思い出す人が多いだろう.そのようなものを電源として使うつもりはないと思っている人もいるかもしれないが,交流の知識は電池を使った電子回路を考えるときにもどうしても必要になってくる.
音声信号は様々な交流信号の重ね合わせだし,電波だってそうだ.電子回路はそのようなものを制御したり,作り出したりもするのである.
そのためにはまず,それがどんなものかを知っておく必要がある.
交流の時間変化
乾電池と抵抗で作った回路を流れる電流は一定で,一方向にながれるのだった.一方,交流は常に大きさが変わる流れである.それどころか,流れる向きまで変わってしまう.一定の周期で,電子が行ったり来たりしているのである.その様子をグラフにすると次のような具合である.
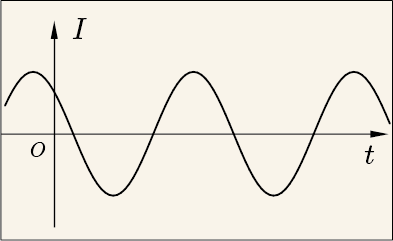
このグラフでプラスの時に右向きに流れているとすると,マイナスの時には左向きに流れていることを意味している.
このように,電流の変化は綺麗なサインカーブを描いている.なぜサインカーブを描いているかと言えば,これは一種の振動,波のようなものだからである.バネにつけたおもりが振動する様子をグラフにすると,これと同じ形になる.
また,紐の先に付けた物体を一定の速度で回転させて,それを回転軸の真上から見ているとき,その左右の動きだけをグラフにすると,これと同じ形になる.
なぜ日本の各家庭にはこのような波打つ流れが届けられているのだろうか.これは発電機の回転と関係がある.発電機の回転で得られた電気は,そのままだと交流なのである.そして,交流は,エネルギーをほとんど無駄に失うことなく電圧の変換ができるという利点もあるので,わざわざ直流に変換することなく届けられているのである.
また,電子回路で人工的に交流を作るときにも,電流の振動を利用するので,自然にこの形になる.
このように,交流がこの形であるのは必然的な理由がある.そしてこれが,理論的にも非常に面白いことになるのである.
表示についての豆知識
直流は英語で Direct Current と言って,直訳すれば「直接的な流れ」である.略して DC と書く.「DC 3V」とか「DC 4.5V」とか「DC 6 V」とか「DC 12V」とかいう表示を良く見かける.
一方,交流は英語で Alternating Current で,直訳すれば「交互に入れ替わる流れ」である.昔は英語の意味通りに「交番電流」と言ったものだが,略されて「交流」となった.略して AC と書く.「AC 100V」という表示は特によく見かける.
脈流
直流電圧と交流電圧とが重ね合わさると,次のグラフのような電圧になる.
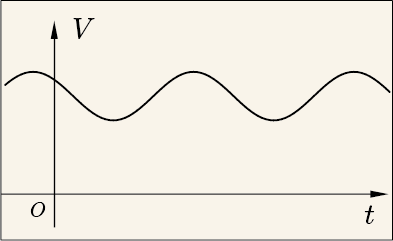
この電圧によって流れる電流は常に一方向に向かって流れるが,その大きさは波打つのである.このような流れのことを「脈流」と呼ぶ.直流でも交流でもないが,どちらをも含む.さまざまな交流を,このような具合にして重ね合わせることができる.
このような電流を作ることによって,一方向にだけしか電流を流して使えない電子部品であっても,信号を増幅したりするのに使えるようになるのである.直流に交流信号を乗せるわけだ.そういうテクニックはあとで徐々に説明していくことにしよう.
重ね合わせたからには,分解して取り出すことも必要になってくる.そういうことも,電子部品を組み合わせることで可能になる.
電子回路というのは,つまるところ,情報をコントロールするための道具であると言えるだろう.
交流を式で表す
電流は情報を運ぶという側面の他に,エネルギーを運ぶという側面もあるので,今回は電力についての話までを一気にして終わることにしよう.
交流電圧は次のような式で表される.
この時,回路に抵抗
のみが繋がっていれば,電圧の変化に全く遅れなく電流が追随することになるので,
という式が成り立ち,次のような同じ形の電流が流れる.
という関係になっているはずだ.理論上,電流は電圧の変化に対して全く遅れが見られない.これは直流回路のところで既に説明した通りである.コイルやコンデンサーがついているとずれが生じるのであるが,その話は後にしよう.現実にはそのような部品がついていなくてもコイルやコンデンサーと同じ要素が勝手に回路に生じているので,ごくわずかなずれが生じる.
や
は「振幅」と呼ばれており,電圧や電流の最大値を意味している.
は「周波数」である.1 秒間に何回同じ波形が繰り返すかを意味している.
秒間では
回だ.三角関数はカッコの中身が
増えるごとに同じ形を繰り返すから,
と書けば,ちょうどその通りの意味になる.
関数はカッコの中身が 0 のときに 0 になるが,
のときに電圧や電流がちょうど 0 だとは限らないので,その調整のために
が付けてある.三角関数のカッコの中身を「位相」と呼ぶ.位相というのは電流や電圧の振動の様子がどの状態にあるかを意味する言葉である.
はその「位相のずれ」を表現するための定数であるが,この
だけを指して「位相」と呼んでしまうこともよくある.その辺りは文脈で判断して欲しい.
ここでは関数を使って表現しているが,
関数を使って表してもいい.どちらも同じ形で位相がずれているだけであるから,
の値を調整すればいいだけの話である.
関数と
関数には次のような関係がある.
それで,どちらで表そうが好きにすればいい.
周波数について
周波数の単位はヘルツである.1 Hz と書いて,1 ヘルツと読む.
日本の家庭用電源は 50 Hz または 60 Hz だが,1 秒間に 50 回あるいは 60 回も,流れの方向が変わっているのである.
とは言っても,導線中の電子の流れは非常にゆっくりなので,実際には大量の電子が導線の同じ所を行きつ戻りつしているイメージである.まさに波に揺れているようなものである.
音声信号は 10 Hz から 20 kHz くらいであり,幅が広い.マイクから出てきた音声信号はこれくらいの周波数を持っている.
電波を扱うようになると,もっと高い周波数の交流を扱うことになる.例えば AM ラジオは 数百~数千 kHz だし,FM ラジオなら 数 MHz ~ 数十 MHz など.携帯電話の電波や無線 LAN の電波は 数 GHz にまで及ぶ.
音声周波数を「低周波」,それ以上を「高周波」と呼んだりするが,明確な決まりがあるわけでもない.
交流の電力
電力は電圧と電流の積で表されるのであった.
これは交流についても成り立つ式である.電圧がプラスの時は電流もプラスであり,電圧がマイナスの時は電流もマイナスである.だから,電力は常にプラスであると言える.電圧がどちらを向いていようとも,電流が抵抗を流れるときにエネルギーが熱に変わる形で消費されるわけだ.
しかし電流は 0 になる瞬間もあるのだから,抵抗は発熱したり止んだりを勢い良く繰り返すことになる.すると,平均すると一体どれだけの電力が消費されていると言えるのだろうか?電力の式は
であるから,このグラフを描いて,一定時間分の面積を求めてやって,その時間で割って平均を出せばいい.面倒だからわざわざ図は描かない.さあ,今こそ積分である.積分というのはこういうときのために使うのだ.楽に計算するには位相のずれは 0 としておいて,1 秒間分の電力の面積を求めて 1 で割る.つまり,こう考えればわざわざ割る必要もないということだ.
途中の計算がややこしい割りに,あっけないほど単純な答が出た.要するに,電圧と電流の最大値どうしの積
では実際の電力を表せておらず,現実の電力はその 1/2 だということになる.これは周波数には関係なく,いつでも成り立つことなのだ.
最大値は最大値でしかないので,交流の電圧や電流の大きさをいつも最大値で表現するのは現実を正確に表せていない.そこで,これも最善の方法だとは言えないのだが,最大値をで割った値を使って表現することにしよう.そうすれば,
となって,現実の平均電力が正しく求められることになる.電圧と電流は比例するのだから,どちらも
で割っておくのは賢いやりかただ.
交流電圧や交流電流の最大値をで割った値を「実効値」と呼ぶ.実効値どうしの積を計算すれば,平均電力が正しく導かれることになる.実効値どうしでもオームの法則は成り立つ.
家庭用コンセントに来ている交流 100 V というのも実効値で表されている数値である.実は,家庭用コンセントには最大値 141 V の電圧が来ているのだ.
最後にひとつ注意しておくが,実効値は,電圧や電流の平均値ではない.電力の平均値にうまく合うように定義されたものである.電圧や電流の値はプラスとマイナスを繰り返すので平均すれば 0 になってしまうし,たとえ絶対値をとってから平均を計算しても実効値と同じにはならない.もし平均値を計算してみれば,それは最大値にを掛けた値になっているはずだ.










