コンデンサーの概要
コンデンサーは,二枚の金属板を少しすき間を空けて向かい合わせた構造の電子部品である.それぞれの板に導線を付けて電圧をかけることで,そこに電荷を蓄積させることができるのである.蓄積できる電荷の量は両端に掛ける電圧に比例する.
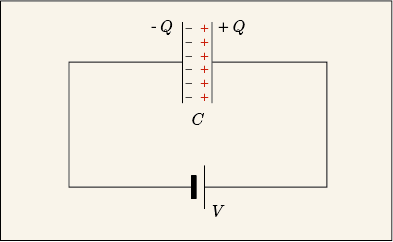
同じ電圧なら,金属板の面積は広いほうが多量の電荷を蓄積できる.また,金属板どうしの幅はなるべく狭くした方が効率よく蓄積できる.なぜなら,間隔が狭い方が,それぞれの金属板の両側に蓄積されている符号の違う電荷が互いに強く引き合ってくれるからだ.
この電荷の蓄積は向かい合わせた金属の表面だけで起こるので,金属板の厚みは要らない.実に,アルミホイルのようなヒラヒラしたものでも構わない.しかしヒラヒラしているとお互いが簡単に接触してしまって,せっかく蓄積した電荷が逃げてしまって困る.そこで間に薄いビニールのような絶縁体を挟むか,あるいは薄いセラミック板の両面に金属を薄く蒸着させてやったりして,なるべく丈夫に,小型化して作る.
二枚の金属の間に挟む絶縁体は,誘電率の高い物質を使った方が効率が良くなる.これは絶縁体内部に生じる電場が,それぞれの電荷が引き合うのを助けてくれるからだ.
以上の話を式で簡単にまとめよう.まず,電圧を強く掛けるほど電荷
が多く貯められるという関係については次のように表現できる.
この
というのはコンデンサーが電荷を貯めることの出来る効率の良さを表すもので,部品ごとに決まる定数である.コンデンサーの性能値だと言って良い.この
のことを,「静電容量」あるいは「キャパシタンス」と呼ぶ.
は Capacitance の頭文字だ.
言い忘れていたが,コンデンサーのそれぞれの板に蓄積される電荷は,それぞれ符号が違うだけの同じ値である.電圧
を掛けた時,片方には
の電荷が,もう片方には
の電荷が蓄積される.
静電容量はファラッドという単位で表される.1 F と書いて,1 ファラッドと読む.1 V の電圧を掛けた時に 1 C(クーロン)の電荷が蓄積できるとき,そのコンデンサの静電容量は 1 F である.
しかし実際にはそんなに多くの電荷を貯めるようなコンデンサを作ることは困難であり,普通は,μF(マイクロ・ファラッド)や pF(ピコ・ファラッド)といった小さな単位で表される.1 μF = 1/1000,000 F であり,1 pF = 1/1000,000,000,000 である.電子部品として実用的に使うには,これくらいの大きさの静電容量で十分なのだ.
同じ原理で電荷を大量に蓄積しておいて,電池のようにして使う目的のものもあるが,それはコンデンサというよりは,「キャパシター」あるいは「スーパーキャパシター」と呼ばれる.
英語では普通のコンデンサについてもキャパシターと呼ぶのが普通である.日本でコンデンサと呼んでいるのはドイツ語を経由したためかもしれない.ドイツ語では Kondensator である.ボルタが,静電気を貯める球形の装置より高い密度の電荷を蓄えられる装置,という意味で使っていた単語が由来らしい.
先ほど,金属板間の距離を小さくするほど静電容量が増すと説明したが,あまり距離を近づけると,金属板間の電場が強くなり,間に挟んだ絶縁体を突き抜けて電流が流れ去ってしまう.「絶縁破壊」と呼ばれる放電現象だ.これが起きてしまうとコンデンサは壊れる.
それでコンデンサの両端に掛けることのできる電圧はそれほど大きくはない.メーカーが保証してくれている限界値のことをコンデンサの「耐圧」と呼ぶ.あまり多くの電気を蓄積しておくことはできないのだ.
容量が大きくて耐圧の高いコンデンサ,あるいはキャパシターは,巨大で,高価である.
電子回路の設計にはあまり関係ないが,静電容量は理論的には次のように表される.
は金属板の面積,
は金属板間の距離,
は間に挟んだ絶縁体の誘電率である.
電解コンデンサー
ほとんどのコンデンサーには極性はない.電池のプラスマイナスを,コンデンサーのどちらの端子に繋ごうとも問題はないということだ.
ただし,電解コンデンサーと呼ばれる部品は,どちらをどちらにつなぐべきかが決まっている.
これは静電容量を稼ぐために,金属フォイルの間に,電解液を染み込ませた薄い紙のようなものを挟んでいるためで,回路図の記号も少し違う.
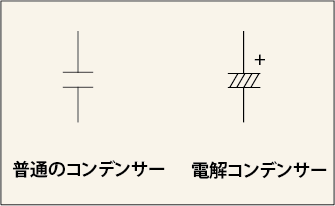
近頃は,普通のコンデンサの記号に+記号を書いただけのものも出てきて,回路図の見た目が面白くない.
長い長いアルミホイルのようなものと,その間に挟んだ湿った紙を,グルグル巻きにして円筒状のケースに詰め込んである.
実はこれは2枚のアルミホイルが金属板の役割をしているのではないし,間に挟んだ湿った紙が誘電体なのでもない.一方のホイルの金属の表面に形成される,ごく薄くて表面積の広い酸化皮膜を,金属板間に挟む誘電体の代わりにしている.そして,もう一方のアルミホイルはただの導線の役割に過ぎず,電解液こそがもう一方の金属板の役目をしている.それで,逆方向に電圧が加えられて余計な化学反応が起きるのを嫌うのである.
高い静電容量を得る代わりに,決して逆方向の電圧が掛からないような場所でしか使えないという,一長一短の性能がなかなかの魅力である.
古い電解コンデンサは内部で気体が発生しており,ケースが膨らんでしまっている.これは「パンク」と呼ばれる状態で,もう壊れてしまっているのである.時には破裂を起こしたり,ケースが割れて内部の液が漏れてしまっていることもある.安全に破裂することができるように,わざと切れ込みを入れてあったりもする.
並列時の合成容量
静電容量を大きくするためには向かい合わせる板の面積を増やせばいいのだった.そのためには,コンデンサーを並列にすればいい.並列に増やすほど,面積は広くなる.
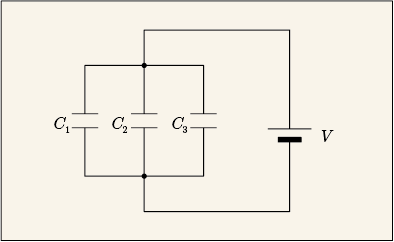
つまり,並列されたコンデンサーの容量は,合計の足し算で表されるのである.
しかしもう少しちゃんと理論的に考えよう.三つのコンデンサーが並列になっているとする.それぞれのコンデンサの両端には同じ電圧が掛かっている.すると,蓄積できる電荷はそれぞれ,
と計算できるであろう.合計の電荷
は
であり,
と
の関係から考えて,全体の
は
だと言えるのである.コンデンサの容量を手軽に増やして使いたいときには並列すればいい.
直列時の合成容量
ではコンデンサを直列にした時には一体どんな結果になるのだろうか.
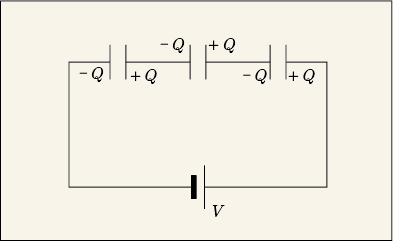
回路の途中の電線に静電気を流し込んで帯電させておくという面倒なことをわざわざしない限りは,直列にしたどのコンデンサにも同じだけの電荷しか蓄えようがない.回路中に釣り合わない余分な電荷が勝手に生じることは無いからである.それで,それぞれのコンデンサの両端に生じる電圧は次のような関係になっている.
回路全体の電圧は,これらを足してやればいい.
直列したコンデンサの両端に見えている電荷は
だけであり,それと回路全体に掛かっている電圧
との関係を
と表したければ,先ほどの式の右辺のカッコを左に移す必要がある.両辺をカッコ内の式で割ってやればいいわけだ.
つまり,全体の静電容量
は
だと考えられるわけだ.これは抵抗を並列にした時の合成抵抗の計算と同じものである.抵抗とコンデンサでは,直列と並列とで計算方法が逆になるというわけだ.










