直列共振
コイルは交流の周波数が高くなるほど電流を流しにくくなり,コンデンサーは周波数が低くなるほど流しにくくなる.ということは,コイルとコンデンサを直列につないでやると,周波数が高すぎず低すぎない中間くらいにちょうどいい周波数があって,その時だけは他の周波数の電流より流れやすくなるのではないだろうか.
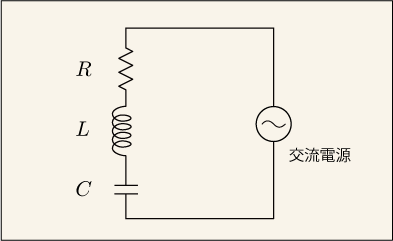
イメージとしてはそんな感じだが,現実に起きることはもっと劇的だ.コイルとコンデンサ
の性質がちょうど打ち消し合って,あたかも抵抗
しか存在しないかのような状態が実現するのである.
RLC直列のインピーダンスは次のように表されるのだった.
コイルとコンデンサーの性質は複素平面の虚数軸上に表されており,お互いに打ち消し合う形になっている.これらがピッタリ打ち消し合えば
だけが残り,インピーダンスは最小になる.その条件を求めよう.
この状態が起きるのは,この条件に合う周波数
のときだけである.この周波数
のことを「共振周波数」と呼ぶ.
これはラジオで特定の周波数の電波だけを拾うのに利用されている.電波がアンテナを通して回路に入ってくることで電流となるが,それは様々な周波数の交流が重ね合わさったものである.そして回路のと
で決まる共振周波数
付近の交流成分は回路を難なく通過できるが,そこから大きく離れた周波数の交流に対しては大きな抵抗があるのと同じで,ほとんど流れることができないのである.
他には,一定の周波数の交流を人工的に作り出すのにも利用される.回路に自然に生じるノイズのうちからこの周波数に合うものだけを取り出して増幅を繰り返すことで,ちょうど共鳴のような状態を起こさせるのである.そのためにはトランジスタが必要になるが,それはあとで説明しよう.
並列共振
今は直列の場合について説明したが,他にどんなつなぎ方が考えられるだろうか.例えば,全ての要素を並列にしてみよう.
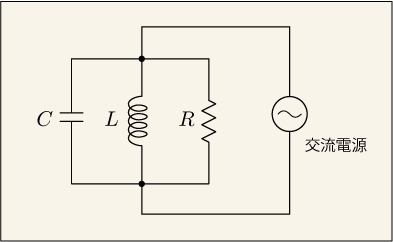
この場合,インピーダンスは次のようになる.
これを変形して実部と虚部に分けるのは少々面倒だが,そんなことをせずとも,
という条件が成り立つところで
となることが分かる.この両辺に
を掛ければ簡単になるだろう.
結果は同じだ.今回も共振周波数は
と
で決まり,直列の場合と同じ式である.
しかしこの時起きていることがまだよく分からない.考えやすいように,抵抗を外してと
だけの並列で計算してみよう.
これは何だろう?ちょっと変だ.ちょうど共振周波数の時に,分母が 0 になってしまうぞ.そうなるとインピーダンスは無限大で,電流は流れないということか.直列共振の時には共振周波数でインピーダンス
が最低になり,電流が一番流れやすかったのに,並列共振の場合には
が無限大になり,電流が最も流れにくくなるのだ.
実はこの時にもコイルとコンデンサーには電流が流れている.コイルとコンデンサーにそれぞれ同じ電圧がかかる時,コイルを流れる電流は 1/4 周期遅れ,コンデンサーに流れる電流は 1/4 周期進み,結局,半周期ずれた形になる.つまり,それぞれが常に逆方向に電流を流しており,しかも共振周波数ではその電流の大きさがぴったり同じなのだ.それで,コイルとコンデンサだけでお互いに同じタイミングで電流をやり取りする形になり,外部からの電流を必要としないのである.
外部から掛けられる電圧のエネルギーの揺さぶりによって,コイルとコンデンサーが互いに共鳴を続ける形になり,しかも外部からの電流を少しも吸い込もうとはしないので,外部から見ればあたかも絶縁体のような状態になっているわけだ.
絶縁体と抵抗とを並列すれば,電流は全て抵抗
に流れ込むので,回路全体の抵抗は
になるというわけである.
並列共振は,共振周波数のときに最も電流を流しにくく,それ以外では流しやすくなっている.直列共振とは逆だ.
もっと単純なイメージで考えてみてもそれほど不思議なことではない.並列の場合,電流は,抵抗,コイル,コンデンサーのうち,最も流れやすいところを通って逃げることができるのだ.周波数が低ければコイルの抵抗は 0 に近付くのでそちらを通ればいいし,周波数が高ければ高いほどコンデンサーを通りやすくなるので,そちらからダダ漏れだというわけだ.
現実的な共振回路の場合
さて,直列でも並列でも共振周波数を求める式は同じだという結果だったが,必ずしもそういう場合ばかりではないということを話しておかないといけない.
次のような回路を考えてみよう.
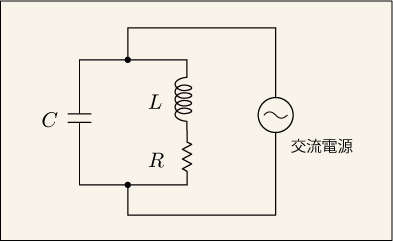
コイルには必ず僅かながらの抵抗が含まれるので,この形の接続を考えるのは現実的だと言えるだろう.インピーダンスは次のように表される.
と
が直列なので合成インピーダンスは足し算で表せて,それと
のインピーダンスを並列で計算するわけだ.これを見る限りでは単純そうなのだが,果たしてこの式の虚数部分が 0 になる条件はどんなものだろうか.
分母の虚数を取っ払って整理するのはなかなかに骨の折れる作業だ.しかし結果だけ書いても何も伝わらない気がするので,面倒だがここでやってしまおう.
やっと求まった.虚数は分子のところにまとめることが出来たので,これで虚数部分が 0 になる条件が求められる.そこには
と
だけでなくて
も混じっていて単純ではなさそうだ.
しかしよく見れば分母にもがあって,事は単純ではない.これでは虚数部分が 0 のときが
の最大や最小を意味するとも言えないわけだ.
抵抗が 0 に近付くほど理想的な並列共振に近付くとは言えるが,理論的に導くのは骨が折れる.こういうものはグラフを描いてやったり,実際に作ったものを測定して調べるほうが楽だろう.
この接続については,次回,もう少し考えてみることにする.
直列共振のイメージ
ところで,直列共振の時に流れやすくなるのはなぜだろう.並列共振の場合にはうまく説明できたが,直列については数式で説明しただけだった.ちゃんと現象としてイメージしてみたい.
直列の場合,電流は共通なのだから,電圧の方にずれが出るのだろう.コイルとコンデンサに掛かる電圧がそれぞれ逆向きになっていて,打ち消し合っている.共振周波数の場合には電圧の大きさが同じであり,ピッタリ打ち消し合う.それでコイルとコンデンサを合わせた部分には電圧が少しも掛かっておらず,全体を外から眺めれば抵抗にのみ電圧が掛かるという形だと解釈できる.それで,全体を流れる電流の大きさを決めるのは,外部から加えられた電源電圧
と抵抗
のみになり,最大の電流が流れるという感じである.










