微分方程式を作る
コイルと抵抗を直列にして電池につないだ回路を考えてみよう.
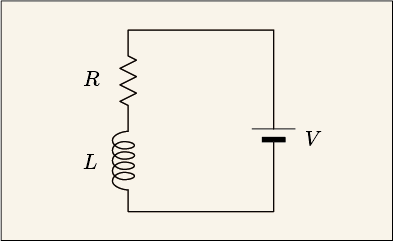
コイルというのはもともと長い導線をグルグルと巻いたものであるから,導線自体の抵抗も無視できない.コイルと導線の抵抗とは切り離せないものなのである.そしてそれは,コイルとは別の抵抗を直列につないだかのように考えても,理論的には大差はない.
もちろん,今からする話は,コイルとは別に,もっと大きな抵抗を直列に付けても同じである.
回路を一周したときの電圧が 0 になるというキルヒホッフの法則を使って式を作ってみる.抵抗では流れた電流によって電圧降下が起きると計算できるし,コイルの両端の電圧は流れる電流の変化に比例するので,次のような式が書き上がる.
電源電圧
も抵抗
も自己インダクタンス
も定数であって,
だけが変数である.これは関数
に関する微分方程式である.
これと同じ形のものはすでに RC 直列回路のところで解いたので計算を飛ばそうと思ったが,それほど難しくもないので書いてしまおう.興味のない人は答えが出るところまで飛ばしてしまっても問題ない.
微分方程式を解く
先ほどの式を整理してみる.
左辺を
だけの式にして,右辺を
だけの式にすれば変数分離形は完成だが,この式には
は現れてないので,左辺に
を持って行くだけでいい.
微分の記号の
と
を分ける.
この両辺を積分するというのが変数分離形の定石だ.
結果はこうなる.
は任意定数である.変形を続けよう.
は先ほどとは異なる任意定数を意味している.
は先ほどとは異なる任意定数を意味している.
これで答えが出た!
は任意定数である.
時定数
ここで,の瞬間に
だという条件を当てはめよう.初めに全く流れていない状態からスイッチを入れて電流が流れ始めるのだから,この条件はごく当たり前の条件に思える.
しかし,スイッチを入れたほぼ瞬間から,オームの法則に従った電流がドッと流れ始めるのではないか,と疑いたくなる気持ちもある.ところがだ,もしスイッチを入れた瞬間に一気に流れ始めるとしたら,電流の変化率は無限大に近いと言えるわけで,コイルには,決して電流を流すまいとする逆方向の巨大な電圧が生じることであろう.そのようなわけで,電流はコイルに生じる電圧のゴキゲンを伺いながら,ゆっくりと流れ始めるしかない.
であれば 0 から徐々に流れ始めるという条件が成り立つであろう.つまり,次のようにまとめられる.
グラフにすると次のような具合である.
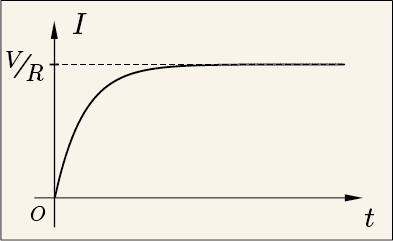
最終的には電流の変化はゆるやかになり,コイルの両端の電圧は 0 に近くなり,まるでコイルなど存在していないかのような状態になる.ただの抵抗だけがつながっているのと同じだけの電流が流れるようになるのである.
のときに
になるから,
秒後には定常電流の 63 % まで流れ始めることになる.
今回のような回路では,この抵抗値と自己インダクタンス
によって決まる時間
のことを「時定数」と呼ぶ.自己インダクタンスが大きいほど,抵抗が小さいほど,安定して流れ始めるのに時間が掛かるのである.
理想と現実
もし自己インダクタンスが 0 だったら,どうなるだろう?
時定数は 0 であるから,瞬時に定常電流に達する.これが,抵抗のみの回路で成り立つ理想的な状況なのである.ところが,自己インダクタンスというのはわざわざコイル状に導線を巻かなくても,導線どうしの配置によって自然発生してしまう.それで,なかなか理想通りに瞬時に設計した電流に到達することはなくて,電流の立ち上がりがわずかに遅れたりするのである.
逆に,もし抵抗が 0 だったらどうなるだろう?
理論上は時定数が無限大になる.これを文字通り受け止めてはいけない.抵抗が 0 なので最終的に回路に無限大の電流が流れようとするところをコイルが阻止しようとしているイメージだ.しかし無限大の電流など流せるわけがない.それ以前に電池にその能力がないのだから電源電圧が下がる.事実上のショートである.
並列回路を考えないわけ
上では抵抗とコイルを直列にしたわけだが,並列にしてみたらどうだろうか?
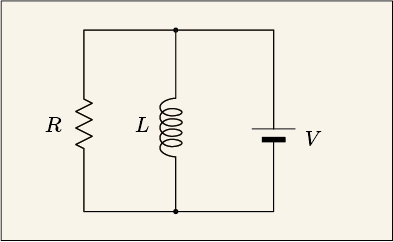
これは厄介な問題だ.というより,問題として成立し得ないのである.
抵抗の両端の電圧はであるから,抵抗の側にはすぐさま一定電流が流れるだろう.しかしコイルの両側の電圧は電流の変化によって決まり,しかもそれが電源電圧と一致しないといけないという矛盾が起こる.先ほどの RL 直列回路で抵抗が 0 の場合にはショートしているのと同じだと書いたが,コイル側の回路は同じような状態である.現実にはコイルにわずかばかりの抵抗が含まれているため,そこまで考えに入れれば計算は破綻しない.
ではコイルの側にごくわずかな抵抗を含めて考えてみよう.
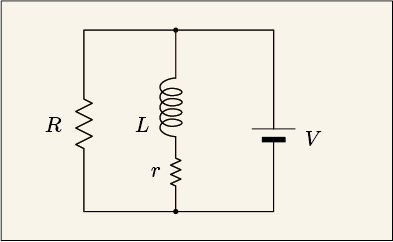
実のところ,これは少しも面白くない.抵抗の両端の電圧はであるから,抵抗の側にはすぐさま一定電流が流れるだろう.そしてコイルの側には,先ほどの RL 直列回路で計算したのと同じ具合に電流が流れる.それだけである.
コイル側の抵抗が小さいので,最終的にコイル側を流れることになる大電流に電源が持ちこたえられればいいのだが・・・.










