角運動量保存の正体
1999 年秋頃に,動きにごまかしのないリアルな巨大ロボットの格闘ゲームを作ろうと思い立った.重心移動などをコントロールする硬派なゲームだ.
今だから言うが,ネット上で格闘大会を主催して,公式改造パーツを「広江工業」の名前で売って一儲けしようと企んでいたわけだ.オーダーメイドも引き受けるつもりだった. しかし当時のパソコンの能力,ネットの遅さを思い出してもらいたい!!またその頃,コンセプトは違うものの,似たようなゲームが連続して発表されたのでやる気が失せてしまった.リモコンダンディとかね.巨大ロボットものは当時流行ったように見えた.開発中の無収入の中で,近いうちに絶対誰かが同じことをやる!という不安に負けたのだった.
金次第でいくらでも強くできるのではなく,指定した材質,強度加工のコストによって値段設定する.形状を工夫することで各パーツの重心位置を調整することができるが,総重量などはサイズ,材質,加工方法の選択によって制約を受ける.ユーザはこれらを専用のソフトで設計して,そこに出た金額を払えば「広江工業製」として認証を受けられて,公式戦で使用可能となるという仕組みだ.また,設計データについてはユーザ間の売買を自由に認めるつもりだった.
とにかくその頃,そのゲームのための基礎的なシミュレーションをコンピュータ上で繰り返していたわけだが,その結果を見て驚いた.運動量の保存のみをプログラムしただけなのに,プログラムした覚えのない物体の回転や遠心力まで再現してくれたのだ.厄介な角運動量保存はどうやってプログラムで実現したらいいのだろうと悩んでいた矢先のことであった.私は暫くの間,なぜプログラムをしてもいないのに角運動量保存がコンピュータ上で再現できているのか理解できないでいた.忠実に角運動量を再現できているわけではないだろう,と疑った時期さえもあった.
私はそれまで角運動量の保存法則は運動量保存法則やエネルギー保存法則と並ぶ宇宙の基本法則の一つでそれぞれは独立して成り立っているのだと思い込んでいたのだ.ところがその辺りを気をつけて教科書を読み直してみると,角運動量保存則は運動量保存法則を使って導かれる結果である事が分かった.運動量保存法則が成り立っている限り,必ず成り立つことが保証されているのである.要は,角運動量保存法則は数学で言うところの定理みたいなもので,公理ではないわけだ.
そんなに難しくないからここでやって見せようか.
最後の行で第 1 項が 0 になるのは,速度ベクトル
どうしの外積を計算したからである.同じ方向を向いたベクトルどうしの外積は 0 になるのだった.このようにして第 2 項だけが残るわけだが,もしこの
も 0 であるなら角運動量は時間的に変化しない事になる.ベクトルを使った場合でも,外部から力のモーメント
が働かない限りは角運動量が保存する事がちゃんと示せるのである.
なぜ角運動量は保存する?
数式で示せるからと言って,それを何も考えずにそのまま受け入れてしまうのは気持ちが悪い.先ほどの式の最後の変形で第 1 項が消えてしまったわけだが,これこそ前回の記事の最後に出てきた疑問の核心部分である.
「回転半径が変化しているのに,なぜ角運動量は変化しないでいられるのか」
ベクトルを使わずに説明した時にはが変化する状況など少しも考慮していなかった.今回は
が自由に時間変化することまで考えて計算したのに,その項はなぜか消えてしまうのである.数学的な理由なんかはどうでもいい.その項が消えてしまっても問題ないことの納得の行く理屈が知りたいのだ.
回転半径が変化しながらなおかつ円運動しているという状態は考えにくいので,次のような想像をしてみよう.自分が宇宙ステーションで船外活動をしている時に何らかの事故があり,命綱が切れてしまったとする.自分は勢い良く宇宙空間へと放り出され,もうお終いかと思ったのだが,運良く命綱の先端がステーションから突き出した丈夫なアンテナに引っ掛かり,何とか一命を取り留めた.どういう具合か,命綱はアンテナに巻き付いては行かないようだ.自分はしばらくの間,そのままアンテナを中心にぐるぐると回る事になった.
この状態で,命綱をたぐり寄せてアンテナに近付こうとしたり,遠心力に負けて手を緩めてしまってアンテナから遠ざかったりするとき,それでも角運動量は保存すると言えるだろうか.
自分が命綱をたぐり寄せてアンテナに近付くための力は力のモーメントにはあたらない.これは回転には何の影響も与えないからである.自分が元の位置の半分近くまでアンテナに近付けば回転半径が半分になるので,角運動量が保存するためには運動量は 2 倍になっていなければならないはずだ.つまり速度が 2 倍.一体何が自分をそこまで加速してくれるだろう?そんな力はどこからも働かないように思える.確かに回転数は 2 倍に速くなるが,それは回転の中心に近付いたために一周の距離が短くなるからであって,自分の速度が変化したわけではない.
ここまでの考えのどこかに誤りがあるのかも知れない.現実の現象を見てみると,実際にこういう場合には運動量は元の 2 倍になるし,回転数(角速度)は 4 倍になる.加速の仕組みは一体どこにあるというのだろうか.
遠心力に逆らって命綱をたぐり寄せるのは考えるべきことが多そうなので,いっそのこと,アンテナから遠ざかる事を考えてみよう.方法はとても簡単だ.手を放せばいい.自分はそのまま今の回転の接線方向へ等速直線運動することだろう.アンテナから見た位置ベクトルの大きさはどんどん大きくなる.これはもはや円運動ではないが,角運動量は定義に従って計算できる.次のような図で説明しよう.
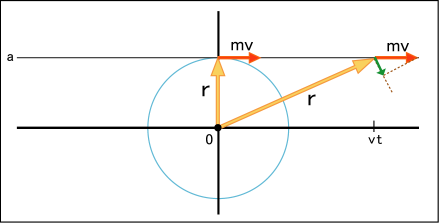
アンテナは原点にあるとする.自分はの地点で命綱を手放し,等速直線運動に入った.
秒後の自分の位置は
である.運動量は常に
のままである.アンテナから見た角運動量を計算してやろう.外積を計算するためには 3 次元で考える必要があるので,
とすればいい.
つまり,時間に関係なくずっと一定だ.こういうことを考えてみた事もない学生が結構いそうだが,角運動量保存則は等速直線運動する物体に対しても成り立っているのである!なぜこんな事になるのだろう.
これを円運動のようにたとえると,確かに回転半径に相当する値は大きくなってゆく.しかし,回転に寄与していると見なせる方向の運動量の成分(上図の緑色の矢印)は同じ割合で徐々に小さくなって行くのである.
これを逆向きに考えたら,先ほどの疑問が解決するだろうか.遠くにいた宇宙の漂流者がだんだんアンテナに近付いてくる.距離はどんどん縮まるが,アンテナ近くをかすめ飛ぶ時には,位置ベクトルに対して直角な運動量の成分は最大になっている.このようにして終始,角運動量は保存する.つまり,角運動量の定義から,有効と見なせる運動量の値に変化があると考えなければならないが故に,角運動量保存が成り立っているわけだ.しかしこんな理屈が,命綱をたぐり寄せて近付くような先ほどの状況にまで当てはめられるだろうか.
それでも何とかやってみよう.アンテナに近付くにはどうしたら良いか.大袈裟に考えてみる.命綱を思い切り引っ張ることで十分な余力を付け,命綱を一瞬手放してジャンプする.つまり手放してからのわずかな時間,等速直線運動と見なせる運動でアンテナに近付くわけだ.次の図のような状況だ.
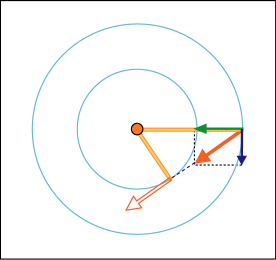
ここで自分はアンテナの方に真っ直ぐ近付く運動量(緑の矢印)を得たつもりでいるのだが,傍から見れば元から持っている運動量(青い矢印)があるので,合計の運動量(赤い矢印)はアンテナの方向をまっすぐ向いていない.
しかしこの合計の運動量(赤い矢印)のまま進めば確実にアンテナとの距離は縮まる.先ほどの等速直線運動の話がそのまま成り立ち,この移動の間,角運動量は変化しない.アンテナに最接近したところで再び命綱をぎゅっと掴めばいい.
緑色の矢印の運動量を得るために使った力は回転方向への加速には寄与しないものだと思われたが,前より大きくなった合計の運動量(赤い矢印)はそっくりそのまま,到達地点での円運動の接線方向の運動量としての意味を持つことになる.これが角運動量が保存するためになくてはならない加速の仕組みである.物体は「わたくしめは運動量保存則にも角運動量保存則にも従わなくてはなりませんから,ここで自らを加速することが必要なのです」などという責任感を持って行動しているわけではないのだ.
角運動量保存則が成り立っている身近な例として,「フィギュアスケーターが伸ばしていた手を縮めると回転が急に速くなる」というのが挙げられることが多い.しかしその理由として,「角運動量は保存するから」という薄っぺらな説明だけしか思いつかない人がもしいるとしたら,自分の理解の浅さを反省した方がいい.もちろん大半の人は分かっていて説明を省略しているに決まっている.
(誰だ?この時の命綱に掛かる張力はアンテナの方向を向いていない,などという間違った理解をしているのは?)
私のこれまでの誤解
現時点で最小の粒子の一つだと考えられている電子でさえスピンと呼ばれる角運動量を持っている.その角運動量の合計は全宇宙で常に一定なのだ,と長年聞かされていた私は回転というのは何か,ミクロからマクロにいたるまで宇宙で特別な根本的な意味を持つ量に違いない,と感じていた.
また,大学の教授によれば,「スピンというのは,ただ角運動量の次元を持つ数学的な量であって,実際に電子が回転しているとは考えるべきではない.」との説明だったので,「うーん,その小さな数学的なスピンが集まって,目に見えるような物体の回転が作られているというのだろうか?その小さな数学的な回転であるスピンと,目に見える普通の回転は一体どの段階でどのようにして結びついているのだろう?理解し難し,角運動量保存則.」という具合に心の底にずっと引っかかっていたのだった.
こうして角運動量の正体に気付いてみると,先ほどの電子のスピンについても謎が氷解する.電子は全宇宙とは関係なく,ただ勝手に回っているだけなのだ.その回転が量子力学的な揺らぎのせいで停められないだけの話なのである.宇宙は全宇宙の回転量が一定になるように管理をしているわけではなかったのだ.
気付いてみると,今までこんな単純なことでつまづいていたのかと自分の理解力の乏しさを痛感する.こんな誤解をしていたのはひょっとして自分だけではないだろうか,と思えてくる.
読者からの反論
この記事を発表して間もなく,幾つかの反論のメールを頂いた.
運動量保存則は空間の平行移動についての対称性から,角運動量保存則は空間の回転についての対称性から,ついでに言えば,エネルギー保存則は時間経過に対する対称性からそれぞれ独立に導かれるはずのものであって,運動量保存則から角運動量保存則が導かれるなどということはないのではないか?というご指摘である.
確かにその通りである.これはネーターの定理といって,何か対称性があるところにはそれに対応して必ず何らかの保存則が対応する,というものである.その指摘以来,私はなぜ運動量保存則だけから導いてきたはずの議論から角運動量保存則が成り立つという結果が導かれることになるのかということについて長い間考えてきたが,ようやく謎が解けてきたようである.
それは制約条件の存在である.運動量から角運動量を作り出したときに,回転半径を導入した.これが運動量保存則に回転対称性という新たな条件を加えることになり角運動量保存則という別の保存則を生み出したのである.
正確にいえば,運動量保存則と角運動量保存則は完全に分離独立しているわけではない.角運動量保存則はその内部に運動量保存則を取り込んでいるのである.この辺りの事情については,次の記事で詳しく説明することにしよう.











この宇宙で特別な意味を持っていると考えなくていい。