ベクトルの利用例
物理でのベクトルの使われ方について少しだけ例を書いておこう.
ニュートンが見出した万有引力というのは,質量が質量を引く力で,その大きさはそれぞれの質量と
に比例し,二つの質量の間の距離
の 2 乗に反比例する.式で表すと次のようになる.
は「万有引力定数」あるいは「重力定数」と呼ばれている比例定数である.この式はすっきりしていて分かりやすいので私は好きだったのだが,大学で学ぶ物理ではあまり使えないものだというのを知ってショックを受けた.力というのは方向があってベクトルで表されるようなものであるが,これでは力の大きさしか表せていないので応用性に欠けるというのである.
さて,どうやったら万有引力がベクトルで表せるだろう?簡単にするために質量が地球のようなものだと考えて,それが座標原点にあるとしよう.そして,質量
の位置を位置ベクトルで表し,
にあるとしてみよう.すると先ほどの式は,ベクトル
の絶対値を使って次のように書ける.
しかしこれでは (1) 式から本質的に何も変わっていない.質量
に働く力の方向はベクトル
の反対方向に働くのだから,(2) 式に
を掛けてやれば力の方向は正しく表せることになるが,それだと力の大きさが正しくなくなってしまう.
で割っておいてやれば,それを補正できるだろう.
3 乗になってしまうあたりが不恰好だが,このような表現はよく使うのである.次のように書けば「2 乗に反比例」というニュアンスを残したままに出来るかも知れない.
この式の一番右にある
という形は,ベクトル
の方向を向いた長さ 1 のベクトルを表すのによく使う表現であり,そこだけ他から分けてみたわけだ.その部分はベクトルの方向を表しているのみであり,力の大きさを表すことには寄与していない.
私は,ベクトルの絶対値を含むこのような表現が不恰好に思えて,慣れるのに苦労した.しかしこのような表現を使っていてもちゃんと具体的な計算をするのに支障がないことを知れば抵抗感は薄れてゆくことだろう.全ては慣れである.
ところで今は質量の方を原点に固定して考えていたが,質量
も動くようなもっと自由度のある議論をしたければ質量
の位置もベクトルで表せばいい.それを
とすると,質量
に働く力は次のように表せる.
大きく変わったように見えるが,(3) 式の
を
に置き換えて配置を変えただけである.思っているものが自由に表現できるようになってくるとなかなか面白いものだ.
位置エネルギーを計算する
重力による位置エネルギーを計算してやろう.高校では位置エネルギーをだと習っているかも知れないが,あれは高さが少々変化しても重力が変わらないくらいの範囲で使えるものである.ここではもっと大きく変化させた場合の位置エネルギーを計算してみたい.
エネルギーというのは仕事のことである.仕事というのは力に逆らって物体を動かした時の距離と力の積で決まる.それで,まずは微小距離だけ動かした時の微小な仕事の大きさを考えよう.あまり長距離を一気に動かすことを考えると,動かしている間に二つの質量の間の距離が変わることで力の大きさが変化してしまうので,単純な式では表せないからである.
今回の記事の目的はベクトルを使いこなす例を挙げることなので,敢えてベクトルでやってみようと思う.微小距離もベクトルを使ってと表すことにする.重力は (3) 式を使って考えることにしよう.重力に逆らって動かす力は
である.仕事というのは掛けた力と,それと同じ方向に進んだ距離を掛けたものなので,内積で表すことになる.
ここでいきなり
というものが出てきているが,この
は物体の位置ベクトル
と,物体の微小移動方向
との方向の違いを表している.ここで,
と置くことにしよう.この
の意味は図で表すと次のようである.
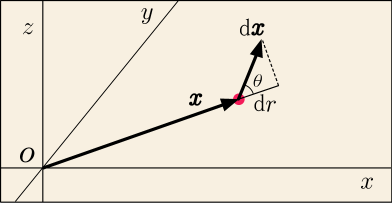
要するに,がどんな方向を向いていようとも,原点からの距離
が変化する分しか計上されないのである.それで
は次のように表せる.
も原点からの距離を表しているのだから,ついでに
に書き換えておいた.この方が分かりやすいだろう.
ここまでのことはわざわざベクトルを使って考えなくても,(1) 式を使って「力に逆らう向きにだけ動かすぞ」と考えれば済むことだった.しかし,どんな方向に動かしてみても
が変化する分しか計算に効いてこないということをちゃんと式で確認できる,ということをやっておきたかったのである.
この微小仕事をを変化させながら足し合わせていけばエネルギーが求められる.
位置エネルギーというのは場所の違いによる差だけが重要なので積分定数
の値は何だって構わないのだが,何だって構わないのなら 0 にしておけばすっきりする.そうすれば
のところで
となるし,そのことを「
は無限遠の地点を基準にして測った位置エネルギーである」とか,もっともらしい表現が出来て説明にも困らない.
位置エネルギーから力を導く
今度は逆をやってみよう.位置エネルギーを微分することで力が導かれるという次の公式が本当に成り立っているのか確かめてみたい.
今,
は
の関数なのにそれを
などで偏微分せよとはどういうことなのか?変数に
が含まれていないならそれは 0 なのではないか?などと考えたりして,学生の頃の自分はなかなか納得できなかったわけだが,
というのは次のような意味なのである.
偏微分というのは「その関数の他の変数を固定」した上で行う微分であって,今回
で偏微分せよと言われた場合には,他の変数というのは
や
のことである.
は
と同列ではないので「
を固定して微分せよ」という意味ではない.そう説明されれば昔の自分は納得できたかも知れないし,ひょっとしてもっと根本的なところから混乱していたので,それだけではまだ納得できなかったかも知れない.
とりあえず,(4) 式の最初の成分だけ計算してみよう.
残りの成分もやることは同じであって,まとめると次のようになる.
これは (3) 式と同じ形であり,めでたしめでたし,だ.










