数学を使わない方法
こまがなぜ倒れないかについては「ジャイロ効果」がその原因であると説明した.そして前回はこの「ジャイロ効果」を角運動量ベクトルを使って説明した.しかしこのような数学的な道具に頼らなくても,もっと簡単に理解する方法があるようである.
これから説明するのは,もう数年前になるのだが,私が前の記事を書いて大満足でいたところにどこかの掲示板で教えて頂いた考え方である.残念ながらそれが誰だったのか,どこの掲示板でのことだったのかさえすっかり忘れてしまった.(アイデアを勝手に拝借したとしても,そろそろ時効成立ってことで許してもらえるだろうか.)とにかく当時なるほどと感心させられたものであり,埋もれさせてしまっては勿体無いので分かりやすくまとめておこうと思った次第である.
慣性力が生み出す力
コマの軸が地面に対して垂直に立って回転しているとする.回転の向きは上から見て反時計回りだとしよう.分かり易いためにこのような状態から考えるだけであって,本当はどんな向きで回っていても構わない.つまり重力の方向は全く関係ない.
このコマを右に倒すとどうなるだろう.コマの縁のいくつかの部分に注目して,その点での運動を考えよう.
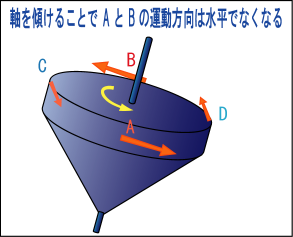
まず,A の部分であるが,もともとは水平方向に運動していた.ところが軸を傾けることにより,斜め下向きに運動方向を変えることになってしまう.逆に B の部分は,もともとは水平に運動していたのが,斜め上向きに運動することになるだろう.C や D の部分については平行移動するだけで,運動方向については全く変化なしだ.
問題は A と B の部分だ.これらの部分は回転軸の向きが変わったからと言って,そう素直に運動方向を変えてくれるだろうか?そうは行くまい.慣性の法則に反するからだ.これらの部分は,なるべく元の運動方向を保とうとするだろう.斜め下に向かうように強制された物体が,回りを引きずってでも無理やり水平に進もうとすれば,この部分一帯は上にせり上がるしかない.そうすることで水平に進み続けられるのだ.
逆に上に向かうように強制されたものは,その部分一帯を下に押し下げることで抵抗するだろう.
つまり,軸を傾けることでこれまで水平運動していた部分が進路を変えられてしまうので,それに抵抗するために全体が図の奥の方へ向かって倒れこむことになる.これがジャイロ効果だというわけだ.
現実に起きているのはこのような分かり易い現象であるのだが,これを前回のようなベクトル表現をすることで,こういう「部分の当然の振る舞い」がすっかり覆い隠されてしまうことになるのである.
ベクトル表現は確かに計算には便利だが,私たちの目を塞いでしまうには十分である.
このような目隠し的状況が最先端物理の数学表現でも起きてはいないだろうかと心配になったりするわけだが,まぁ,偉そうに人の心配をするよりも,自分がさっさと最先端にたどり着く事の方が優先的課題だろう.










