学生がつまづく原因
慣性モーメントで学生がつまづくまず第一の原因は,積分計算のテクニックが求められる最初のところであるという事である.高校までの積分の範囲では,積分の後についてくるとか
とかいう記号が
で積分しなさいとか
で積分しなさいとかいう事を表すだけの単なる飾りくらいにしか扱われていない.それがいきなり大学で
とかになってもこれは体積全体について足し合わせることを表す単なる象徴的な記号であって,具体的な計算は不可能だと思ってしまうのである.3 重積分などが出てくるともうお手上げである.まず,この辺りの考えを叩き直さなければならない.本当はすごく簡単なのだ.
学生がつまづくもうひとつの原因は,慣性モーメントと同時に出てくる「重心の位置を求める計算」である.これらの計算内容は形式的にとても似ているので重心と慣性モーメントをごっちゃにして混乱してしまうようなのである.
慣性モーメントの意味の確認
前の記事で慣性モーメントがと表せることを説明したが,これは大きさを持たない質点に適用される話であって,大きさを持った物体が回転するときには当てはまらない.形と広がりを持った物体の慣性モーメントを求めるときには,その物体が質点の集まりであることを考えて積分計算をする必要がある.
なぜ慣性モーメントを求めたいのかをはっきりさせておこう.動機は大切である.慣性モーメントは「回転運動における質量」のような概念であって,力のモーメントと角加速度との関係をつなぐ係数のようなものである.物体の慣性モーメントを計算することが出来れば,どれだけの力がかかったときにどれだけの回転をするのかを予測することが出来るので機械設計などの工業的な応用に大変役に立つのである.もちろん理論的な応用も数限りないので学生にはちゃんと身に付けておいてもらいたいと思うのである.
もうひとつ注意しておかなくてはならないことがある.慣性モーメントの大きさは,物体の質量や形だけで決まるものではなく,回転軸の位置や向きの取り方によっても値が大きく変わってくるということである.回転軸は物体の重心を通っている必要はないし,物体の内部を通る必要さえない.一般に軸が重心を離れるほど,慣性モーメントは大きくなる.バランスよく回るかどうかは慣性モーメントとは別問題である.
しかし普通は,重心を通る回転軸のまわりの慣性モーメントを計算することが多い.これには理由がある.一つは,何も支えがない宇宙空間などでは物体は重心の周りに回転するからこれを知るのは大切なことであるということ.もうひとつは,重心を通る軸の周りの慣性モーメントさえ求めておけば,あとで話す「平行軸の定理」というものを使って,軸が重心から離れた場合に慣性モーメントがどのように変化するのかを瞬時に計算することが出来るので,大変便利だという理由もある.
そこで,これから具体例を一つあげて軸が重心を通る時の慣性モーメントを計算してみることにしよう.
積分計算の意味
半径,厚さ
で,密度
の円盤の慣性モーメントを計算してみよう.この例を選んだ理由は,計算が難し過ぎなくて,かつ役に立つ内容が含まれているので教育的に良いと考えたからである.

まず円盤が質点の集まりで出来ていると考え,その円盤の中の小さな一部分が持つ微小な慣性モーメントを求めてそれを全て足し合わせることを考える.
つまり,式で書くと全慣性モーメントは次のように表せるということだ.
この積分記号
は全ての
を足し合わせるという意味であり,数学の
記号と同じような意味で使われているのである.ちなみに
記号も
記号も和 (Sum) の頭文字の S を使ったものである.(
はギリシア語の S である.)
記号と
記号の違いは足し合わせる量が離散的か連続的かというだけのことなのである.
ではこのを具体的に計算してゆくことにしよう.この物体の微小部分が作る慣性モーメント
は,その部分が位置する中心からの距離
とその部分の微小な質量
を使って,
と表せる.この微小質量
はその部分の密度と微小部分の体積をかけたものであり,
と表せる.それで,これまでの内容をまとめて式で表せば,
となるのであるが,このままではまだ計算できない.微小体積
を別の変数で表す必要がある.どのように表したらよいだろうか?
これは座標系のとり方によって表し方が変わってくる.もし直交座標であるならば,微小体積は,微小な縦の長さ,微小な横の長さ,微小な高さを掛け合わせたものであるので,と表せる.つまり,
ということになり,ここで 3 重積分が出てくるわけだ.しかし,3 重になったからといって怖れる必要は全くない.3 重積分の計算方法は,中から順番に,まず
で積分してその結果を
で積分してさらにその全体を
で積分すればいいだけである.
このとき,積分する順序は気にしなくても良い.多分このようなことを平気で言うから「物理屋は数学を全然分かってない」と言われるのだろうが,普通の物理に出てくる範囲では積分順序を入れ替えたくらいで結果は変わらないのでこの程度の理解で十分なのだ.
よくの代わりに
という略記をする教官がいるが,わざわざ
と書くのが面倒なのでそうしているだけである.こういう初心者への心遣いのなさが学生を混乱させる原因となっているのだと思う.しかし
と書く以外にうまく表現できない事態というのもあるので,この書き方が良くないというわけではない.(最近ではベクトルを使って
と書くことが増えたようである.)
では,今の 3 重積分を計算してみよう.まずその前に,半径を直交座標で表現しておかなければ計算できない.色々と面倒なことがあるものだ.半径は
なので,
は,
と表される.ところがここで困ったことに,積分範囲をどうとるかという問題が起きてくる.
については円盤の厚さを取ればいいから
までの範囲で積分すればいい.しかし
と
の範囲は円形領域なので気をつけなくてはならない.領域全てを隈なく覆い尽くすような積分範囲を考える必要がある.そこで
の積分範囲を
として,
を含んだ形で表し,
の積分範囲を
とする必要がある.
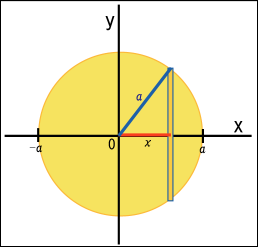
こうなると積分の順序を気にしなくてはならなくなる.まずで積分し,次にその結果を
で積分するのである.
さて,これを計算すれば答えが出ることは出る.しかし今更だが私はこんな面倒くさそうな計算をするのは嫌である.もっと簡単な計算方法があるのだ.
円筒座標を使う
円筒座標を使えば,はるかに簡単になる.円筒座標というのは平面を極座標の
と
で表し,
をそのまま使う座標系である.こうすれば
で積分出来るので半径
をわざわざ
と
とで表し直す必要がなくなる.積分範囲も難しいことを考えなくても済む.
ところで円筒座標での微小体積はどう表せるだろうか?次の図を見てもらいたい.
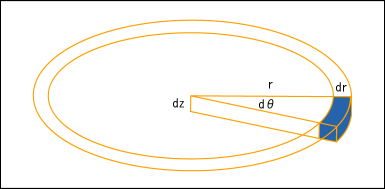
この青い領域は極めて微小な領域であると考える.原点からの距離と比べると
というのは誤差程度でしかない.するとこの領域は縦が
,横が
,高さが
の直方体であると見ることが出来るだろう.もちろんこの領域は厳密には直方体ではないのだが,直方体との誤差をもし正確に求めたとしたら,それは非常に小さいのだから,
にさらに
などが付いた形として求まるだろう.微積分というのは,これらの微小量を無限小にまで小さくした状態を考えるのであって,誤差なんかは求めたい部分に比べて無限に小さくなると考えられるのである.
それでと書くことが出来る.よって全体の慣性モーメントを式で表せば,次のようになる.
これを
と
と
について順番に積分計算すればいいだけの事である.この場合,積分順序を気にする必要はなくて,
を
まで,
は
まで,
は
の範囲で積分すればいい.
3 重積分や,微小体積を微小長さの積として表す方法について理解してもらえただろうか?積分計算はこのようにやるのである.積分の最後についているや
や
にはこのような意味があって,単なる飾りではないのだ.
他の場合について知りたければ各自努力してもらいたい.今言った方法を使っていろんなことが出来るはずである.3 次元球座標におけるがどのように表せるかは他の入門的教科書に図入りで載っているのでそっちを調べてもらいたい.縦,横,高さがそれぞれ,
,
,
の直方体で表せるので
と置けば良い.
平行軸の定理
一般に回転軸が重心を離れるほど慣性モーメントは大きくなる,と前に書いた.これについては大変便利な公式があって「平行軸の定理」と呼ばれている.軸が重心を通る時の慣性モーメントさえ分かっていれば,その回転軸を平行に動かしたときの慣性モーメントはそれに
を加えるだけで求められるのである.
ここで
は物体の全質量であり,
は軸を平行に移動させた距離,すなわち軸が重心から離れた距離である.
は重心を通っている場合の値に限る.それ以外の場合にはこの公式は使えない.
なぜ「平行軸の定理」と呼ばれているかについても良く考えてもらいたい.軸の傾きを変えると物体の慣性モーメントは全く違った値を示すのである.この公式は軸を平行移動させた場合にしか使えない.










