慣性モーメントテンソル

動機と準備

第 3 部では,回転軸からだけ離れた位置にある質点の慣性モーメントがと表せる理由を説明した.多数の質点が集まっている場合にはそれら全ての和を取ればいいし,連続したかたまりについて計算したければ各点の位置と密度を積分すればいい.このを使えば角速度と角運動量の間にという関係が成り立つのだった.

しかしこれでは不便なところがある.一旦回転軸の方向を決めてその軸の周りの慣性モーメントを計算したら,その値はその回転軸に対してしか使えないのである.まぁ当たり前の話ではある.軸の方向を変えたらその都度計算し直してやればいいだけの話だ.それで満足できる人はそれでいい.この先も読まなくてもいい.

しかし回転軸の方向をほんの少しだけ変更したらどうなるのだろう.元から少しずらしただけなのだから,慣性モーメントには少しの変化があるだけに違いない.わざわざ一から計算し直さなくても何か楽に求められるような関係式が成り立っていそうなものである.

それがちゃんとあるのだ.ある軸について一旦計算しておきさえすれば,「ほんの少しずらした場合」にとどまらず,どんな方向に変更した場合にでもちょっとした手続きで新しい慣性モーメントが求められるという素晴らしい方法だ.もちろん楽をするためには少々の複雑さには堪えねばならない.

回転軸を色んな方向に向ける事を考えるのだから,軸の方向をベクトルで表しておく必要がある.角速度ベクトルと角運動量ベクトルを次のように拡張しよう.今後はベクトルは太字で表すことにする. このベクトルの意味について少し注意が必要である.例えば, と書けば,軸の周りに角速度 ω_x で回転するという意味であるとしか考えようがないから問題はない.それでは,次のようになった場合にはどう解釈すべきだろう. 軸を中心に ω_x で回転しつつ,同時に軸の周りにも ω_y で回転するなどというややこしい意味に受け取ってはいけない.軸が回った状態で軸の周りを回るのと,軸が回った状態で軸の周りを回るのでは動きが全く違う.そのような複雑な運動を一つのベクトルだけで表せるだろうと考えるのは非常に甘いことである.

ここは単純に, (ω_x, ω_y, 0) の方向を向いた軸の周りを,角速度で回っている状況だと理解するべきである.この計算ではは負値を取る事ができないが,逆回転を表せないのではないかという心配は要らない.というのも,軸ベクトルの向きが回転方向をも決めているからである.「右ネジの回転と進行方向」と同様な関係になっていると考えれば何も問題はない.逆回転を表したければ軸ベクトルの向きを正反対にすればいい.

素人考え

記号の準備が整ったので,すぐにでも関係式を作りたいところだ.,,軸それぞれの周りに物体を回した時の慣性モーメント I_x , I_y , I_z をそれぞれ計算してやれば, という 3 つの式が成り立っている.それで,これを行列を使ってのように配置してやれば 3 つ全てを一度に表してやる事が出来るだろう.後はこれを座標変換でグルグル回してやりさえすれば,回転軸をどんな方向に向けた場合についても旨く表せるのではないだろうか.

これは基本的なアイデアとしては非常にいいのだが,すぐに幾つかの疑問点にぶつかる事に気付く.例えば, (ω_x, ω_y, 0) という回転軸で計算してやると, となって, I_x =I_y でもない限り,との方向が違ってきてしまうことになる.角運動量が,実際に回転している軸方向以外の成分を持つなんて,そんなことがあるだろうか？

また,上に出てきた行列は今は綺麗な対角行列になっているが,座標変換してやるためにはこれに回転行列を掛けることになる.すると非対角要素が 0 でない行列に化けてしまうだろう.そうなると変換後は,,軸についてさえ,との方向が一致しなくなってしまうことになる.こんな事でいいのだろうか.この考えは本当に使えるのだろうか？

閃きを試してみる事はとても大事だが,その結果が既存の体系と矛盾しないかということをじっくり検証することはもっと大事である.しかし一度おかしな固定観念に縛られてしまうと誤りを見出すのはなかなか難しい.最初から既存の体系に従っていけば後から検証する手間が省けるというものだ.直観を重視するやり方はどうしても先へ進めない時以外は控えめに使うことにしよう.

定義に忠実な関係式

こういう時は定義に戻って,ちゃんとした手続きを踏んで考えるのが筋である.角運動量ベクトルの定義は,外積を使って, と表せる.この定義についてはここでは説明しない.外積については電磁気学のページに出ているので,そこからこの式の意味するものを掴んで欲しい.ここでは質点の位置を表す相対ベクトルであり,何を基準点にしても構わない.この式では基準にした点の周りの角運動量が求まるのであり,基準点をどこに取るかによって角運動量ベクトルは異なった値を示す.

一般的な理論では,ある点の周りに自由にてんでんばらばらに運動する多数の質点の合計の角運動量を計算したりするのであるが,今回の場合は,ある軸の周りをどの質点も同じ角速度で一緒に回転するような状況を考えているので,そういうややこしい計算をする必要はない.慣性モーメントは「剛体の回転」を表すという特別な場合に威力を発揮するように作られた概念なのである.

さて,剛体をどこを中心に回すかは自由である.必ずしも重心を基準にする必要もない.

上で出てきた運動量ベクトルの定義は p=mv と表せるが,この速度ベクトルは角速度ベクトルを使って, と表せる.つまり,まとめれば,との間に, という関係があるということである.外積は掛ける順序や並びが大切であるから勝手に括弧を外したりは出来ない.これにはちゃんと変形の公式があって,きちんと成分まで考えて綺麗にまとめれば, となることが証明できる.有名な公式を使っただけである.ここでもし第 1 項だけだったなら,はと同じ方向を向いたベクトルとなっていただろう.ところが第 2 項は方向のベクトルである.いや,マイナスが付いているからの逆方向だ.その合成ベクトルがだというのである.

これは驚きだ.物体は,実際に回転している軸以外の方向に,角運動量の成分を持っているというのだろうか.ちょっと信じ難いことだが,定義に従う限りはこれこそが正しい結果だと受け止めるべきである.しかしなぜそんなことになっているのだろう.

それを考える前にもう少し式を眺めてみよう.このままだと第 2 項が悪者扱いされてしまいそうだ.2 つの項に分かれたのは計算上のことに過ぎなくて,両方を合わせたものだけが本当の意味を持っている.しかし 2 つを分けて考えることはイメージの助けとなるので,この点は最大限に利用させてもらうことにする.

さて,第 2 項のにだって,と同じ方向成分は含まれているのである.もし第 1 項だけだとしたらまるで意味のない答えでしかない.そのことが良く分かるように,位置ベクトルの成分を (x,y,z) と書いて,上の式を成分に分けて表現し直そう. これを行列で表してやれば次のような,綺麗な対称行列が出来上がる. ここに出てきた行列こそとの関係を正しく結ぶものであり,慣性モーメントの 3 次元版としての意味を持つものである.これを「慣性モーメントテンソル」あるいは短く略して「慣性テンソル」と呼ぶ.

これは先ほど単純な考えで作った行列とどんな違いがあるだろうか.まず 3 つの対角要素に注目してみよう.左上からそれぞれ,,,軸からの垂直距離の 2 乗に質量を掛けたものになっていることが読み取れよう.つまり,,軸についての慣性モーメントを表しているわけで,この部分については先ほどの考えと変わりがない.

先の行列との大きな違いは,それ以外の部分,つまり非対角要素である.前の行列では 0 だったが,今回は何やら色々と数値が入っている.これを「慣性乗積」と呼ぶ.第 2 項のベクトルの内,と同じ方向のベクトル成分を取り去ったものであり,をの方向からずらしている原因はこの部分である.

慣性乗積が 0 にならない理由は何だろうか.この部分は物理的には一体何を表しているのだろうか.

慣性乗積の意味

慣性乗積というのは,方向を向いたベクトルの内,方向成分を取り去ったものであると言えよう.しかもマイナスが付いているからその逆方向である.図に表すと次のような方向を持ったベクトルである.

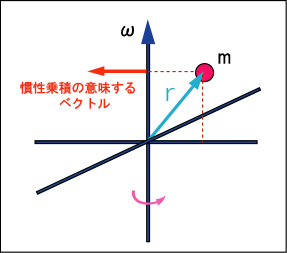
もしマイナスが付いていなければ,これは質点にかかる遠心力が軸を質点の方向へ引っ張って,引きずり倒そうとする傾向を表しているのではないかと短絡的に考えてしまった事だろう.しかしこのベクトルは遠心力とは逆方向を向いており,なぜかを遠心力とは逆方向へ倒そうとするのである.この理由を説明できなくてはならない.

遠心力と正反対の方向を向いたベクトルの正体は何か.そもそもこの慣性乗積のベクトルが,本当に遠心力に関係しているのかという点を疑ってみたくなる.それで第 2 項の係数を良く見てみると, m(r・ω) となっている.つまりベクトルがと同じ方向を向いているほど値が大きくなるわけだ.しかしがあまりにに近い方向を向いてしまうと,その大部分が第 1 項と共に慣性モーメントを表すのに使われるので,慣性乗積は小さ目になってしまうだろう.

そして逆にとが直角を成す時には値は 0 になってしまう.図で言うと,質点が回転の中心と水平の位置にあるときである.この状態でも質点には遠心力が働いているはずだ.それなのに値が 0 になってしまうとは,やはり遠心力とは無関係な量なのか！

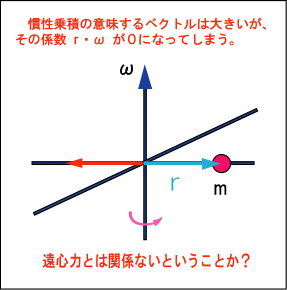
現実の物体を思い浮かべながら考え直してみよう.質点が回転中心と同じ水平面にある時にだって遠心力は働いている.そのとき,その力で何が起こるだろうか.引っ張られて軸は横向きに移動するだろう・・・.そうだ！この状況では回転軸は横向きに引っ張られるだけで,横倒しにはならない.慣性乗積は軸を傾ける傾向を表していると考えたらどうだろう.回転への影響は中心から離れているほど強く働く.つまり遠心力による「力のモーメント 」に関係があるのではないか.

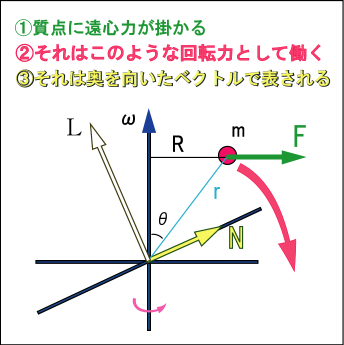
検証してみよう.遠心力の大きさは F=mRω^2 で表される.ここでは軸からの距離である.との成す角をとすると, R=rsinθ である.そして,力のモーメントはの回転方向成分と,原点からの距離をかけたものだから,

一方,慣性乗積の部分が表すベクトルの大きさ |P| は m(r・ω)r の内,の成分を取っ払ったものだから, という事で両者はただ倍の違いがあるだけで大変良く似た形になる.このような違いがあるのは当然である.「力のモーメント」と「角運動量」は次元の異なる量なのだから,一致されては困る.ここで,「力のモーメントベクトル」というのは,理論上,を微分したものであるということを思い出してもらいたい.が次の瞬間,どちらへどの程度変化するかを表したのがなのである.

「力のモーメント」のベクトルは「遠心力による回転」面の垂直方向を向くから,上の図で言うと奥へ向かう形になる.一方,角運動量ベクトルは慣性乗積の影響で左上に向かって傾いている.この状態から軸がほんの少し回ったら,は軸の回転に合わせて少し奥へ傾く事になるだろう.

微小時間の間に微小角だけ軸が回転したとすると,は |P| dφ だけ奥へ向かうだろう.それをで割れば,を微分した事に相当する.つまり, |P| dφ/dt =|P|ω であって,先ほどの倍の差はちゃんと説明できる.

つまり,がこのような傾きを持っていないと,という回転力の存在が出て来ないのである.別には遠心力に逆らって逆を向いていたわけではないのだ.数式というのはいつだってそうだ.我々のイメージ通りの答えを出してはくれるとは限らず,むしろ我々が気付いていない事をさらりと明らかにしてくれる.

角運動量保存

これで角運動量ベクトルが回転軸とは違う方向を向いている理由が理解できた.しかし大きな問題が残されている.すでに気付いていて違和感を持っている読者もいることだろう.外力もないのに角運動量ベクトルが物体の回転に合わせてくるくると向きを変えるのだとしたら,角運動量保存則に反しているのではないだろうか,ということだ.

大丈夫.角運動量保存則はちゃんと成り立っている.どうしてだろうか.実は,角運動量ベクトルは常に同じ向きに固定されていて,変わるのは,なんと回転軸の向きの方なのだ！

ここまでの話では物体に対して回転軸を固定するような事はしていなかった.ただ,ある一点を「回転の中心」と呼んで,その周りの運動を論じていただけである.つまり,物体は角運動量を保存するべく,回転軸の方向を次々と変えることが許されているのである.

ここで「回転軸」の意味を再確認しておかないと誤解を招くことになる.実はこの言葉には二通りの解釈が可能だったのだが,ここまでは物体が方向を変えるなんて考えがなかったからその違いを気にしなくても良かった.どう説明すると二通りの回転軸の違いを読者に伝えられるだろう.

例えば物体が宙に浮きつつ,軸を中心に回っていたとする.しばらくしてこの物体を見たら姿勢を変えて回っていた.姿勢は変えたが相変わらず軸を中心に回っていたとする.ちゃんと状況を正しく想像してもらえただろうか.この時,回転軸の向きは変化したのか,しなかったのか,どちらだと答えようか.

「回転軸の向きは変化した」と答えて欲しいのだ.とは物体の立場で見た軸の方向なのである.上の例で物体は相変わらず軸を中心に回っているが,これを「回転軸」と呼ぶべきではない.そう呼びたくなる気持ちは分かるが,それはが意味している方向ではない.では客観的に見た場合に,物体が回転している軸（上で言うところの軸）を何と呼べばいいのだろう.そんな心配は必要ない.それこそ角運動量ベクトルが指している方向なのである.

との向きに違いがあることに違和感があったのは,この「回転軸」という言葉の解釈を誤っていたことによるものが大きかったと言えるだろう.これで全てが解決したわけではないことは知っているが,かなりすっきりしたはずだ.

何も支えがない物体がここで説明したような動きをすることについては,実際に確かめられている.有名なのは,宇宙飛行士の毛利衛さんがスペースシャトルから宇宙授業をして下さったときのもので,その中に「無重量状態下でペンチを回す」という実験があった.その貴重な映像はネット上で見ることが出来る.「ペンチ」「宇宙」などのキーワードで検索をかけてもらうとたどり着けるだろう.ペンチの姿勢は次々と変わるが,回転の向きは変化していないことが分かる.是非探して自分の目で確かめて欲しい.このような映像を公開してくれていることに心から感謝する.

なお紹介した映像はその利用規定が厳しく,ここのような個人サイトからのリンクが禁じられている.私が教育機関の教員でもなく,このサイトが学校の授業の一環として作成されたのでもないために条件を満たさないのである.不便をかけるが,個人的に探して貰いたい.なお,読者が個人的に探し当てたサイトが,私が意図しているサイトであるかどうかを確認するヒントとして,以下の文字列を書き記しておくことにする.

http://www2.edu.ipa.go.jp/gz2/d-etu1/d-muj1/d-mrj1/IPA-etu130.htm

物体の回転姿勢が変わるたびに,回転軸と角運動量の関係が次々と変化して,何とも予想を越えた動き方をするのである.

行列の意味するもの

慣性モーメントというのは質量と同じような概念である.質量というのは力を加えた時,どのように加速するかを表していた.同じように,回転させようとした時にどの軸の周りに回転しようとするかという傾向を表しているのが慣性モーメントテンソルである.慣性乗積が 0 でない場合には,回転させようとした時に,別の軸の周りに動き出そうとする傾向があるということが読み取れる.

ここまでは質点一つで考えてきたが,質点は幾つあっても互いに影響を及ぼしあったりはしない.全て対等であり,その分だけ重ね合わせて考えてやればいい.よって広がりを持った物体の全慣性モーメントテンソルは次のようになる. もしこの行列の慣性乗積の部分がすべてぴったり 0 となってくれるならば,それは多数の質点に働く遠心力の影響が旨く釣り合っていて,軸がおかしな方向へぶれたりしないことを意味している.ただし,気を付けないといけない.軸が重心を通っていない場合には,たとえ慣性乗積が 0 であろうとも軸は横ぶれを引き起こすだろう.慣性乗積は軸を傾ける度合いを表しているのであり,横ぶれの度合いは表していないのである.

工業製品や実験器具を作る際に,回転体の振動をなるべく取り除きたいというのは良くある話だ.軸が重心を通るように調整するのは最低限しておくべきことではあるが,回転体の密度が一定でなかったり形状が対称でなかったりする場合に慣性乗積が全て 0 になるなんて偶然はほとんど期待できない.

それで仕方なく,軸を無理やり固定して回転させてみてはどうかということになるのだが,あまりがっちり固定してしまっては摩擦で軸は回らない.よって少しのアソビを持たせることがどうしても必要になるが,軸はその許された範囲で暴れまわろうとすることだろう.軸受けに負担が掛かり,磨耗や振動音が問題になる.

重りをどのように追加したら重心位置を変化させないで慣性乗積を 0 にすることができるか,という数学的な問題とその解法がきっとどこかの教科書に載っているのだろうが,具体的応用にまで踏み込まないのがこのサイトの基本方針である.軸のぶれの原因が分かったので,数学に頼らなくても感覚的にどうしたら良いかという見当は付け易くなっただろうと思う.

工学的な困難に対する同情は十分したつもりなので,申し訳ないが物理の問題に戻ることにする.

このように軸を無理やり固定した場合,今度こそ,回転軸と角運動量の向きの違いが問題になるのではないだろうか.先ほどは回転軸の方が変化するのだということで納得できたが,今回は回転軸が固定されてしまっている.今度こそ角運動量ベクトルの方がぐるぐる回ってしまって,角運動量が保存していないということになりはしないだろうか.

そのような問題は起こらない.いつでも数学の結果のみを信じるといった態度を取っていると痛い目にあう.この場合,計算で求められた角運動量ベクトルの内,固定された回転軸と同じ方向成分が本物の角運動量であると解釈してやればいい.との方向は一致しているのだ.

根拠のない人為的な辻褄合わせのようで気に入らないだろうか.ちゃんと釈明はできる.例えばある質量の物体に力を加えてやれば加速度の値が計算で求まるだろう.ここでもし,物体がその方向へ動かないように壁を作ってやったらどうなるか.計算上では加速するはずだが,現実には壁を通り抜けたりはしない.だから壁の方向への加速は無視して考えてやれば,現実の運動がどうなるかを表せるわけだ.それと同じ事をしたまでだ.

しかしこのやり方ではあまりに人為的で気持ち悪いという人には,物体が壁を押すのに対抗して壁が物体を同じ力で押し返しているから力が釣り合って壁の方向へは加速しないんだよ,という説明をしてやって,理論の一貫性が成り立っていることを説明できるだろう.

これについても同じことが出来る.物体が姿勢を変えようとするときにそれを押さえ付けている軸受けが,それに対抗するだけの「力のモーメント」を逆に及ぼしていると解釈できるので,その方向への角運動量は変化しないと考えておけばいい,と言えるわけだ.

結局,物体が固定された軸の周りを回るときには,行列の慣性乗積の部分を無視してやって構わない.慣性乗積は回転にぶれがあるかどうかの傾向を示しているだけだ.よって行列の対角成分に表れた慣性モーメントの値にだけ注目してやればいい.物体はこの値に応じた勢いで回る.ぶれと慣性モーメントは全く別問題である.

回転軸が,,軸にぴったりの場合は,対角成分にあるそれぞれの慣性モーメントの値をそのまま使えば良いが,軸が斜めを向いている場合,例えば (ω_x, ω_y, 0) の場合にはとの方向が一致しない結果になるので解釈に困ったことがあった.しかし,この場合もと一致する方向のの成分との大きさの比を取ってやれば慣性モーメントが求められることになる.

そんな方法ではなくもっと数値をきっちり求めたいという場合には,傾いたを座標変換してやって,,軸のいずれかに一致させてやればいい.

座標の回転

テンソルはベクトルとの関係を定義に従って一般的に計算したものなので,どの角度に座標変換しようとも問題なく使える.

そのために回転行列を使う.この行列の具体的な形をイメージできないと理解が少々つらいかも知れないが,今回の議論の本質ではないのでわざわざ書かないでおこう.書くのが面倒なだけで全く難しいものではない.数学の教科書でも見てもらいたい.

とにかく,とを共に同じ角度だけ回転させてというベクトルを作り, L=Iω の関係を元にして,との間の関係を導くのである.そのためには次のようにすればいい. つまり新しい慣性テンソルはと計算してやればいいことになる.

ところでここで,純粋に数学的な話から面白い結果が導き出せる.対称行列をこのような形で座標変換してやるとき,「を対角行列にするような行列が必ず存在する」という興味深い定理がある.

これが意味するのは,回転体がどんなに複雑な形をしていようとも,慣性乗積が 0 となるような軸が必ず 3 つ存在している,ということだ.そのような特別な回転軸の方向を「慣性主軸」と呼ぶ.それらはなぜかいつも直交して存在しているのである.これは直観ではなかなか思いつかない意外な結果である.

どんな複雑な形状の物体でも,向きをうまく選びさえすれば慣性テンソルが 3 つの値だけで表されてしまう.つまり,3 軸の慣性モーメントの数値のみがその物体の回転についての全てを言い表していることになる.物体の回転を論じる時に,形状の違いなどはほとんど意味を成していないのだ.なんて単純な話だろう.

そして回転体の特徴を分類するとすれば,次の 3 通りしかない.

3 軸全ての慣性モーメントの値が等しい場合.
3 軸の内,2 つの慣性モーメントの値が等しい場合.
3 つの慣性モーメントの値がバラバラの場合.

それぞれ,上から「球状コマ」「対称コマ」「非対称コマ」と呼んで区別する.

球状コマというのは,3 方向の慣性モーメントが等しければいいだけなので,別に物質の分布が球対称になっていなくても実現できる.単に球と同じような性質を持った回り方をするという意味での分類でしかない.球状コマはどの角度に向きを変えても慣性テンソルの形が変化しない.対角行列のままである.例えば慣性モーメントの値がだったとすると, となるからである.つまり,軸をどんな角度に取ろうとも軸ブレを起こさないで回すことが出来る.

次に対称コマについて幾つか注意しておこう.例えば I_x =I_y ≠I_z である場合,これは軸が軸に垂直でありさえすれば,どの方向に向いていようとも軸ぶれを起こさないということになる.もちろん,軸が重心を通っていることは最低限必要だが・・・.典型的なおもちゃのコマの形は対称コマになってはいるが,おもちゃのコマはここで言うところの軸の周りに回して遊ぶものなので,対称コマとしての性質は特に使っていないことになる.

対称コマの典型的な形は軸について軸対称な形をしている物体である.しかし軸対称でなくても対称コマは実現できる.この「対称コマ」という呼び名の由来が良く分からない.「軸に対して軸対称な物体と同じ性質の回転をするコマ」という意味なのか,「面内のどの方向に対しても慣性モーメントの値が対称なコマ」という意味なのか,どちらの意味にも取れてしまう.

回転の安定性

教科書によっては「物体が慣性主軸の周りに回転する時には安定して回る」と書いてあるものがある.この「安定」という言葉を誤解しないように気をつけないといけない.これはただ「軸ブレを起こさないで回る」という意味でしかないからだ.

慣性主軸の周りに回っている物体の軸が,ほんの少しだけ,ずれたとしよう.そもそも,完璧に慣性主軸の方向に回転し続けるなんてことは有り得ない.現実にどうしてもごく僅かなズレは起こるものだ.

非対称コマの場合がもっともひどい.非対称コマはどの方向へずれようとも,それがほんの少しだけだったとしても,慣性テンソルは対角形ではなくなってしまう.つまり軸がぶれ始める.軸がぶれて軸方向が変われば,慣性テンソルはもっと大きく変形してぶれはもっと大きくなる.

球状コマだって無関係ではない.確かに,軸がずれても慣性テンソルの形は変わらないので,軸のぶれは起こらないだろう.しかし,復元力が働いて元の位置に戻ろうとするわけではない.軸が一度ずれればずれたままだ.

この安定は非常に不安定なのだ.

このような不安定さを抑えるために軸受けが要る.ぶれが大きくならない内は軽い力で抑えておける.ぶれが大きくならないように一定の範囲に抑えておかないといけない.

なぜこんなことをわざわざ注意するかというと,この慣性主軸の概念というのは「コマが倒れないで安定して回ること」とは全く別問題だということに気付いて欲しいからである.

コマが倒れないで回っていられるのはジャイロ効果による.外力によって角運動量ベクトルが倒されそうになる時に,それ以上その方向に倒れ込まないような抵抗を示すから倒れないのである.これがジャイロ効果である.

一方,今回の話は軸ぶれについてであって,外力は関係ない.内力によって回転体の姿勢は変化するが,角運動量に変化はないのである.

ではおもちゃのコマはなぜいつまでもひどい軸ぶれを起こさないでいられるのだろう.おもちゃのコマは対称コマではあるものの,対称コマとしての性質は使っていないはずなのに.

これは,軸の下方が地面と接しており,摩擦力で動きが制限されているせいであろう.好き勝手に姿勢を変えたくても変えられないのだ.

磁力で空中に支えられて摩擦なしに回るコマのおもちゃもあるが,これは磁力によって復元力が働くために,姿勢が保たれて,ぶれが起こらないでいられる.本当の無重量状態で支えもない状態でコマを回せば,コマは姿勢を変えてしまうはずだ.

平行軸の定理

ここまでは,どんな点を基準にして慣性テンソルを求めても問題ないと説明してきたが,実は剛体の重心を基準にして慣性テンソルを求めてやった方が,非常に便利なことがあるのである.それは,以前「平行軸の定理」として説明したような定理が慣性テンソルについても成り立っていて,重心位置からベクトル a=(a_x ,a_y ,a_z ) だけ移動した位置を中心に回転させた時の慣性テンソルが,重心周りの慣性テンソルを使って簡単に求められるのである. この定理の正式名称を私は知らない.もはや平行移動に限らないので平行軸の定理とは呼ばないと思う.なぜこのようなことが成り立っているのか,勘のいい人なら,この形式を見ておおよその想像は付くだろう.勘のそれほどよくない人でも,本気で知りたければ,専門の教科書を調べる資格が十分あるのでチャレンジしてみてほしい.健闘を祈る.