電荷は等速運動している時には電磁波を放射しないことが分かった.加速運動をする時にだけ電磁波を放射するのである.それは一本のビームのように一方向だけに出て行くわけではなく,かと言って全方向に均等に放射されるのでもない.方向によって強さに差があり,ある方向にはほとんど出て行かないということもある.
電磁波は運動量を持つので,それが全方向に均一に出て行かないということは,電荷にはその反作用が加わる事になるだろう.自ら作り出した電磁場から力を受けるというので,これを「自己力」と呼ぶわけだ.
その放射される電磁波の強度分布は,リエナール・ヴィーヒェルト・ポテンシャルから苦労して電場や磁場を計算し,そこからポインティング・ベクトルを計算する事で導かれるわけだが,結果だけをここに引用するのが申し訳なく思えるほどその過程は面倒だ.
教科書によって見た目が大きく違っていたりするが,なるべく見やすくなるようにそれぞれ略記号を工夫してしているせいであって,展開すると結局同じになるのでそれほど心配は要らない.(ただし単位系の違いによって係数に違いが出ることはある.)ここでは
は点電荷の位置から観測点の方を向いた単位ベクトルであり,
は点電荷の位置から観測点までの距離である.
は速度ベクトル.
は加速度ベクトルである.
少し注意が必要なのは,右辺の変数は全て,電荷が電磁波を発した過去の時刻の値であるということだ.電荷が移動しながら電磁波を放つ場合に,その効果が遠方でどう重なり合うかを計算したい場合にはこのことを気をつけないといけないが,今回はある瞬間に電荷からどの方向にどの程度の電磁波が出て行くかを知りたいだけなのでそれほど気にしなくてもいい.
条件によって色々な放射のされ方があるのが読み取れるだろうか.加速の強さ,方向だけで決まるのではなく,その時の電荷の速度,方向によっても変わってくるらしい.つまり一つの図だけでまとめて表すのは難しいということだ.
ここでは幾つかの典型的な例についてだけ簡単に話すことにしよう.
進行方向に平行な加速
まずは,電荷の運動と同じ方向に加速を受ける場合について.
これは例えば垂直に立てたアンテナの中を電子が上下に行き来する場合がそうだ.アマチュア無線などをやっておられる方は,電波がどちらへ強く放射されるかは経験的に良くご存知だろう.(プロの方は知っていて当然である.)これはアンテナを軸として全方向に均等に出てゆくのである.真上から見るとそのように見えるのだが,横から見ると方向に分布があるのが分かる.真上,真下には放射されず,水平方向に特に強く放射されるわけだが,斜め上や斜め下にも弱いながら出てゆく.
しかしこれは電子の速さが光に比べて非常に遅い時だけの話である.速度が変わると同じ事をしても放射される方向が変わる.それが良く分かるように強度分布図を描いてみよう.
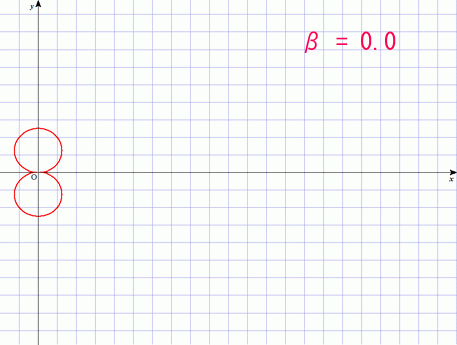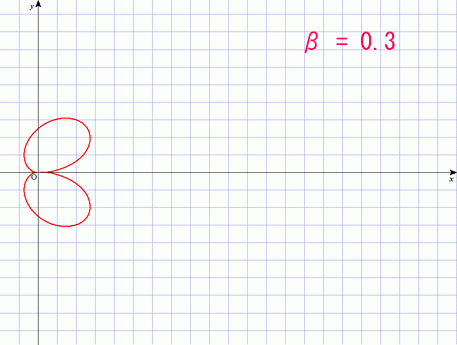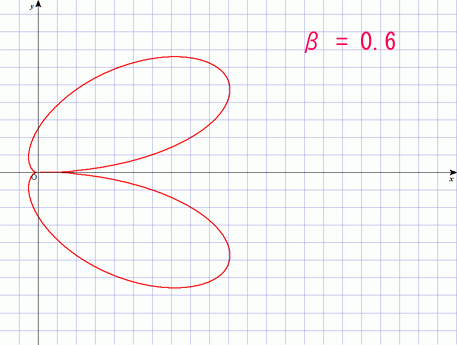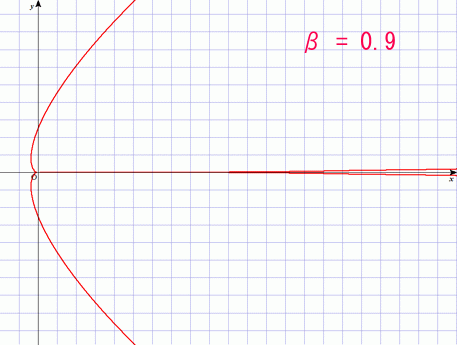
の場合が,上のアンテナの話に相当する.速度と加速度はともに横軸に取ってあるので,アンテナを横に向けた状態を表している.
しかし光速近くまで加速した電子を加速あるいは減速してやると,進行方向に偏った強烈な電磁波が発生するようになることが分かるだろう.この現象を「制動放射」と呼ぶ.実はレントゲン写真に使う X 線というのはほとんどがこの原理で発生させている.
どうやるかというと,高電圧の電極で電子を加速させ,それを勢い良く金属にぶつけてやる.すると電子は金属表面の電子と反発して急減速し,そのときに強烈な光を発生するのである.この高エネルギーの光が X 線だ.このように単純な方法で発生させることが出来るので,昔の実験家は知らず知らずの内に大量の被曝をしたことだろう.
進行方向に垂直な加速
では,電子の進行方向とは垂直方向に加速をした場合にはどうなるだろう.この時には進行方向に向かって最も強く光を放つようである.
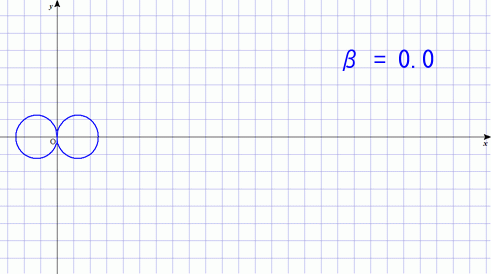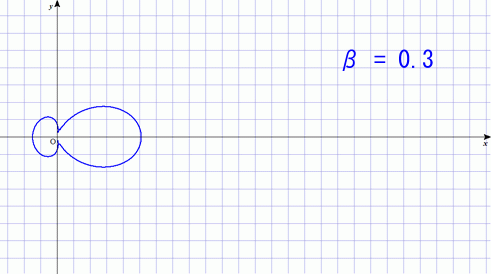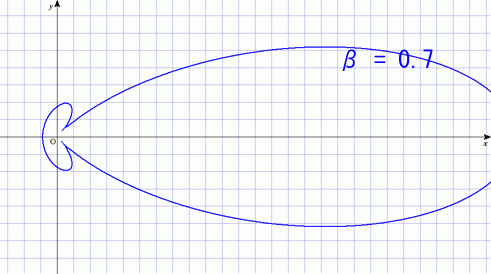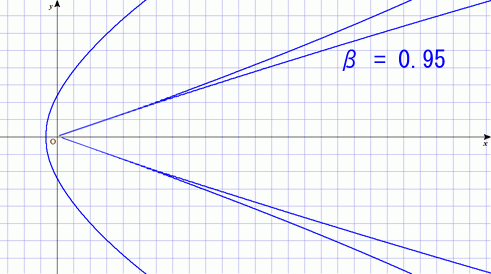
の場合は先ほどのアンテナの話と同じ状態である.今回は加速度が
方向なので向きが違うだけだ.これが,
が大きくなるにつれて,先ほどとは違う形に変わってゆくのが面白い.
光速に近い電荷の場合,同じ加速をしただけなのに強烈な放射をすることが分かる.この現象はリング状の粒子加速器を運用する上で問題になる.繰り返し加速を行わせたいので,荷電粒子に円軌道を回らせているのだが,そのために磁場を使って軌道を曲げてやる必要がある.その時に,このタイプの放射が起こる.これを「シンクロトロン放射」と呼ぶ.加速に使ったせっかくのエネルギーの大半を電磁波として放射してしまうのだ.
科学者が巨大な円形加速器を建設しようとしているのは,このような放射によるロスを防ぐために軌道の曲がりをなるべく少なく済ませたいからである.しかしこのシンクロトロン放射は単なる邪魔者だというわけではなく,医療や科学実験に非常に役に立つ性質を持っており,よく利用されているという側面もある.
このタイプの放射の存在を知っておくことは原子の構造を理解する上で非常に重要である.1911 年,ラザフォードが原子の中に原子核を発見した時,電子はこの原子核のプラス電荷に引かれて,原子核の周りを回っているのだという説が有力候補として浮上した.中学や高校では原子というのはそのような構造になっているのだと習うだろう.
しかし当時の科学者たちは「そんな構造は絶対に在り得ない」と反対した.なぜなら,もし電子が原子核の周りを円軌道で回っているとすると,上と同じ原理によって電子は強烈な電磁波を放ち,電子はたちまちにしてエネルギーを失って原子核に墜落してしまうと考えられるからである.
これは当時の科学者たちを非常に悩ませた問題であった.円軌道は在り得ないとは言っても,他のいい説が思い浮かばないのである.しばらくは試行錯誤のぎこちない理論が提案され,やがて量子力学によって,電子が波として存在すると考える事でようやく解決されたのである.義務教育で習う,原子核の周りに同心円を描いたような単純な原子の構造は,100 年近く前の科学者たちが即座に大反対して捨て去ってしまった古いモデルなのである.しかし現実の原子と似た面もあるというので,今でもよく利用される.
よく考えるタイプの生徒がこのモデルに疑いを抱き,そこでつまづいてしまって成績を落としてしまったりすることがたまにある.愚かな事よ・・・.時には妥協も必要だ.
図の描き方
今回のような強度分布図を描くのはパソコンがあればそれほど難しいことではない.の面での断面図を描きたいので,
と
の関係を求めてやって,陰関数グラフを描けばいいだけである.ありがたいことに,陰関数グラフを描いてくれるようなソフトが無料で公開されているのでそれを使わせてもらうことができる.
具体的には
などと置いて計算すればいい.
「進行方向に平行な加速」の場合には次のような式になる.
ただし,
は他の係数などと一緒に変数
としてまとめてしまってある.これで
が一定となる曲線が描けるというわけである.後は
の値・・・すなわち
を 0 ~ 1 まで動かしてやればいい.
の値をいじってやれば,大きさが調整できる.
「進行方向に垂直な加速」の場合には次のような式になる.
コンピュータに負担のないようにもう少し変形できそうだが,計算内容が読者に分かる程度にとどめておいた.










