疑問
電荷が移動すると周囲の電場に変化がある.電場が変化すれば磁場が生じるのだった.磁場が新たに生じるというのは,磁場の強さに変化があったということだから,それによってさらに電場が生じるだろう.
そんな具合にして次々と伝わって行くのが電磁波である,と前に説明した.上のような連鎖は電荷が等速運動しているときにだって起きていていいはずだ.しかし等速運動する電荷が電磁波を放っているとなると納得の行かない事が出てくる.電磁波というのはエネルギーを持っているから,エネルギーが次々に出て行ってしまうことになるのではないだろうか.そのエネルギーはどこから供給されているのかの説明が付かない.
等速運動する電荷を放っておくとそのうちエネルギーを失って勝手に止まってしまうということがあるだろうか.もし止まるとしても一体,何に対して止まるというのだろう.電荷と一緒に動いている人にとって見れば電荷は止まっているわけだが,これが勝手に速度を変えたりするものだろうか.
実はそのような心配は一切要らない.等速運動する電荷からは電磁波が出ないことがもう 100 年も前から理論的に分かっているし,それに反する事例もこれまで見付かってはいない.一体,どういう理屈でそんなことが言えるのだろう.今回はそれについて説明したい.
計算とイメージ
そのために前回出てきた「リエナール・ヴィーヒェルト・ポテンシャル」を使う.軸方向へ速度
で等速運動する点電荷が,時刻
に原点
を通過したとする.この電荷が時刻
に
地点に作る電磁ポテンシャルを求めてやる.
この問題を解くには少々の工夫が必要になる.単純にやろうとすると分母に含まれるベクトルの絶対値の扱いや過去の電荷の位置などを考えている内に,式は複雑になってくるわ,気が付けば数時間が無駄に過ぎているわで,イライラしてくる.そうならないための賢い解法は教科書に頼ってもらうことにして,とにかく正しく導くことが出来れば次のような結果を得る事になる.
以前の計算には
という要素が入っていたが,この結果にはそういうものがなくてすっきりしている.この式の中に
というのがあるが,
は点電荷の現在位置だと考えられる.つまり,
は観測点と点電荷の現在の相対位置を表していることになる.この結果の面白さが見えているだろうか?過去に電荷がいた位置からの遅延を考えるという面倒な見方を捨て去ってしまって,現在の電荷の位置と電磁ポテンシャルの形を対応させた形になっているのである.
上の式は少し面倒な形をしているが,軸上に立って観測していると
であるから,すっきりした式になる.これは静止している電荷が作る静電ポテンシャルと変わらない形だ.あたかも静止している時の電荷と同じ形の静電ポテンシャルが電荷と一緒に近付いてくるように見えることだろう.しかし
軸上からずれたところで観測すると少し様子が違う.静止している電荷よりも強い影響があるように感ずるのである.
このままではイメージを描きにくいかも知れないから,電荷の位置を中心とした等電位面を描いてみようか.
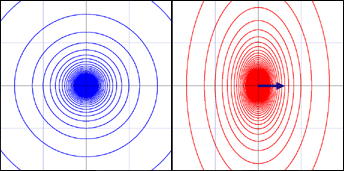
半透明の楕円球が幾層にも重なるような美しい絵を描けたらいいのだが,そのようなセンスがないので,断面図で我慢して欲しい.左側の同心円は比較のために描いた静止した電荷が周囲に作る静電ポテンシャルであり,右側が等速運動する電荷の周りの静電ポテンシャルである.
何と点電荷が,このような形の電磁ポテンシャルを常に自身と同じ速度で引き連れて移動しているようなイメージになっているのだ.前回は電荷の移動する前方では影響が強く現れ,後方では弱くなると説明したが,この表現では電荷の前方にも後方にもポテンシャルが対称な形で存在しているのである.「前方に影響が強く現れたように見えたのは,それを観測する頃には電荷が実際に観測点に近い位置に来ていたのだから当然ではないか」という少々強引な見方もできるということである.
ところで,この図から電場ベクトルの向きを勝手に想像してはいけない.「電場ベクトルの向きは等電位面に垂直になる」だとか「等電位線が密なところほど電場が強い」などというルールは,静電場の場合にしか通用しないのである.時間変化があるときの電場は次の式によって計算されるのだった.
今は
も存在している以上,静電ポテンシャル
だけでは電場の値は決まらないのである.この式によって電場を計算してやると,結果は次のようになる.
少しでも分かり易くなることを願って,点電荷からの相対位置を
として書き直してやろう.
という要素が全体に掛かっているので,静止時よりも全体的に電場が小さくなっていることがすぐに読み取れるが,それだけではない.電場の向きは電荷を中心にしてどこまでも真っ直ぐに外を向いているのである.つまり,電気力線はまっすぐだということだ.何とまぁ,イメージが随分違うではないか!しかし電場の大きさは球対称にはなっていない.進行方向の前後に離れると,力の大きさは急激に弱くなるのである.これは先ほどの等電位線の密度から想像されるのとは逆の傾向である.
教科書ではこの傾向を「進行方向に潰れた回転楕円体」だと表現してあるが,式を見るとそれほど単純な形では無さそうだ.気になったので強度分布を図にしてみた.
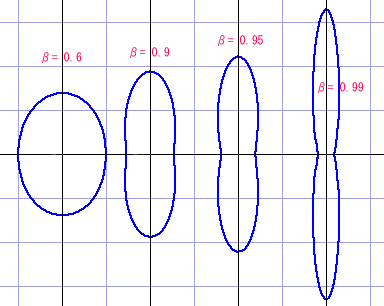
電場の絶対値が同じ値になるところを線で結んで描いてある.いろんな速度について並べてみた.である.普通は回転楕円体だが,電荷が光速に極めて近付いたところでは中央が薄くなった丸ざぶとん型になるようである.
さて,磁場はどうなっているだろうか.磁場はで導かれる.先ほどの
の式の分母には
が入っていたが,今は
なので,
や
は 0 だということだ.つまり磁場の
方向のベクトルは 0 であり,
軸に垂直な面内で
軸の周りに渦を巻く格好になることが読み取れる. もう少し計算テクニックを駆使してやると次のような簡単な式で表すことも出来るらしい.
つまり,まるで電流の周りに発生する磁場のように
軸の周りを回るように存在しているが,電荷から離れるほど弱くなる.しかし別に具体的な何かが回転しているわけではないから,らせん状に突き進むドリルのようなイメージを思い描くのは少し違う.ただ,そのような向きを向いている場が,電荷の接近と共に強くなり,通り過ぎると再び弱くなるというだけのことだ.
「電荷に近付くほど強い」とは言ったものの,との外積で表されることから,
軸に近付くほど 0 に近くなるという傾向も併せて持つであろう.この微妙な分布がどういう形になるのか気になったので,これも強度分布を図にしてみた.
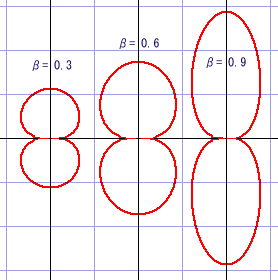
なるほどねぇ.
結論
以上の議論によって大体何が起こっているか分かっただろう.初めに書いたように,電荷の移動によって電場は変化するし,それによって磁場も変化する.しかしその磁場の変化が別の新たな電場を生み出して連鎖するというイメージはあまり正確ではなかったことになる.電場と磁場の変化はそれぞれ互いにマクスウェル方程式を満たすように存在するだけであり,それが安定した形を保って電荷と共に移動するのである.
もし電荷が無限の過去からずっと等速運動を続けていたならば,無限の遠方に至るまで電場と磁場がずっとこの形で宇宙に広がっており,それが一斉に電荷に並走するかの如くに振舞うことだろう.同じ状態を保ったまま平行移動するだけなので,エネルギーはいつまで経っても電荷から遠く離れては行かない.よって新たなエネルギーは必要ないのである.
しかしこれは波動方程式の妙により,あくまでも「そう見える」だけだ.あるとき突然に電荷が速度を変えれば,この見かけの安定は崩れ,電荷が速度を変えたという情報は光速度で周囲へ伝わるだろう.その知らせが届くまでは遠方の電磁場は相変わらず以前の速度に合わせて進んでいる.電磁場は別にどこまでも電荷に合わせようと忠誠を誓って行動しているわけではなくて,結果としてそうなっているだけだからだ.
電荷が再び別の等速運動に落ち着けば,宇宙の電磁場は新しい秩序によって徐々に塗り替えられる.その先頭に立つのが電磁波であり,この変化を伝える波がエネルギーを光速で無限の彼方まで運び去るのである.











そのネタはまだ後に取っておく。