困った事態
微分形のガウスの法則の右辺には電荷密度が出てくる.
電荷密度
は位置の関数である.場所によって電荷の密度が決まるという意味である.
多数の電荷が雲のように集まった状態を遠くから眺めるような場合には,このような密度による扱いは大変役に立つ.ところがもっと対象に近付いて,電荷を持った個々の粒子について論じようとすると,この形式はやっかいである.
粒子に有限の大きさがあると考えるような場合ならば,電荷が内部に一様に分布していると考えたり電荷密度が中心からの距離の関数として表せるなどと仮定することも出来るだろう.しかし素粒子について論じるときや,他のものに対して大きさが無視できるとする場合などのように粒子の大きさが一点であると考えたい場合には密度は使えない.電荷を持つにも関わらず粒子の大きさが 0 であるということは,電荷密度が一点のみで無限大になることを意味するからである.
それでもガウスの法則を使いたいときにはどうしたらいいだろうか.
お気楽解決
そこで登場するのが「デルタ関数」である.電荷密度が一点で無限大になるなら,それをそっくりそのまま表してやる関数を作ってやればいい,というわけだ.その定義は次の通りである.
関数の中身が 0 になる時に値が無限大になるので,
の点に電荷が存在することを表したければ
としてやればいい.
本当にこんな単純に電荷密度を表しただけで問題が解決したのだろうか?いや,まだまだ問題がある.電荷密度をある範囲で積分すれば,その範囲にある全電荷量が求められるはずだ.だからこのデルタ関数を積分した時には,ちゃんとその一点に存在する電荷量が求められなければいけないはずなのである.そこでお気楽に次のような条件を加えておこう.
なぜ積分の結果が 1 になるようにしたかというと,こうしておけば,電荷が
の点に存在する時の電荷密度を表すのに
という具合に書いておけるからである.これを積分すれば,結果は
になって,ちゃんと積分範囲に含まれる電荷の大きさが導かれるというわけだ.
イメージ
まぁデルタ関数なんてのは上で説明したくらいのものなのだが,一点だけで無限大で,積分すると 1 になるなんてイメージがわかないという人がいるかも知れないのでちょっとだけ補足しておこう.
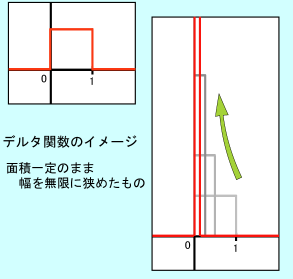
次のような関数を考える.が 0 から 1 までは値が 1 で,それ以外は 0 となるような関数だ.下に図を付けておこう.これを積分すれば値は 1 になる.なぜなら,積分は関数が作る面積だから.
この関数のでっぱりの面積を一定にしたまま幅を狭くしてやって,幅を極限まで 0 に近づけたものがデルタ関数だと考えればそれほど無理な考えでないことが分かるだろう.
しかしこのイメージが全てだと考えていると失敗する.例えば,
なんて関数も積分の値は
の値に関わらず 1 になる(複素関数論を使って計算する)し,
関数は
の極限では
に比例する形の関数になるので分子と分母で打ち消しあって有限の値
になる.そこで
の極限を取ることでデルタ関数と似た性質を実現できる.
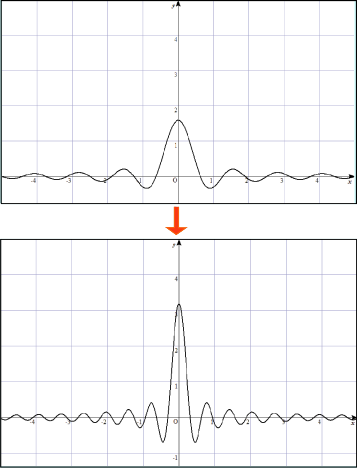
このような近似式は他にいくらでも考えられるのだ.
私が学生の頃の話だが,講義の中でいきなり上に出した関数による近似式を使われたので,「なぜデルタ関数をそうやって変形できるんですか?」と質問したことがあるが,「そんな当たり前のことも分からないのか?」と笑われただけだという苦い思い出がある.ああ,やだやだ.
戸惑う数学者
こんな関数を考え出したのは一体誰かというと,あのディラックである.ディラックの名前はこの後の解説でもあちこちで出てくる予定だが,変なことをする天才である.彼の論理は非常に危うくて大胆だが間違っちゃいない,というので,「アクロバティック(曲芸)・ディラック」という異名を取るほどだ.その内,分かる.(笑
(ディラック方程式,ブラケット記号,モノポールの存在仮説,巨大数仮説など)
さて,デルタ関数などという奇妙なものを関数として認めてしまうと,これまで関数の性質として論じていたことが当てはまらない事柄が出てきてしまい,数学的にいろいろな不都合が発生してしまうことになるらしい.(どういう不都合かは私には詳しく語れない.)しかし,デルタ関数が便利に使えて,論理的に破綻しているわけではないのも確かだ.
そこで数学者は渋々これを認め,これは関数とは別のものであるという意味合いを込めて「超関数」というものに分類することにした.英語では distribution と呼ばれており,function とは別物扱いだ.日本語の「超関数」という表現は意味を捉えたものであって的外れというわけではない.そしてこれは数学の一分野にもなった.
ディラックという人は全く(良い意味で)人騒がせな人である.
この関数はここに書いた以外にも微分ができたり,フーリエ変換ができたりと,なかなか面白い性質があるのだが,とりあえずはこれくらいの理解で十分であろう.興味のある人は調べてみるといい.










