電磁気学：電気双極子モーメント

この解説の動機

絶対値の等しい正電荷と負電荷が少しだけ離れて置かれているところをイメージしてほしい.この二つの電荷をまとめて「電気双極子」と呼ぶ.

電荷間の距離は問わないが,ペアとして一体となって存在しているかのように扱いたいので近いほうがいい.かと言って全く同じ場所にあれば二つの電荷は完全に打ち消し合ってしまうから,少しだけ離れていてほしい.

さて,この電気双極子が周囲に作る電気力線はどのような形になるだろうか.この二つの電荷を一本の棒の両端に固定してやったイメージを考えると,まるで棒磁石が作る磁力線に似たものになりそうだ.

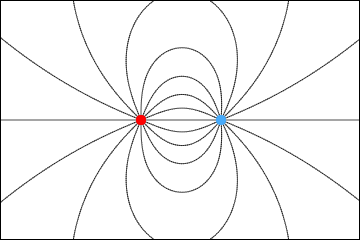
二つの電荷の間の距離が極めて小さければどうなるだろう？それを十分に遠くから離れて見る場合には正と負の電荷の値がぴったり打ち消し合っており,電場は外に少しも漏れてこないようにも思える.いや,実際はどうなのか？少しは漏れてくる気がするし,漏れてくるとしたらどの程度なのだろう？

ここで話そうとしている内容は以前の私にとっては全く応用の話に思えて,わざわざ記事にする気が起きなかった.しかし量子力学の話をしていると粒子が作る磁気モーメントの話が重要になってくる.磁気モーメントとこれから話す電気双極子モーメントの話は似ているから,先に簡単な電気双極子モーメントの話を済ませておいた方が良いだろうと判断するに至ったのである.

電気双極子のエネルギー

これから具体的な計算をするために定義をはっきりさせておこう.との電荷が空間にあって,の位置からの位置に引いたベクトルをとしよう.この時,次のようなベクトルを「電気双極子モーメント」と呼ぶ. 電気双極子モーメントの電荷は全体としては 0 なので,一様な電場中で平行移動させてもエネルギーは変わらない.ベクトルの方向を変えることによってエネルギーが変わる.

電気双極子モーメントのベクトルが電場と垂直な方向を向いている時をエネルギーの基準にしよう.エネルギーというのは本当はどの状態を基準にしてもいいのだが,こうするのが一番自然な感じがしないだろうか？正電荷と負電荷が電場の方向に対して横並びになっているから,それぞれの位置エネルギーがちょうど打ち消し合っている感じがする.これは私個人の感想だから意味が分からなければ忘れてくれて構わない.

この状態から回転して電場と同じ方向を向いた時,それぞれの電荷は電場の向きに対してはちょうど s/2 の距離だけ互いに逆方向に移動したことになる.電場に従うように移動したのだから,位置エネルギーは下がる.エネルギーは移動距離と力を掛け合わせて計算するのだから,正電荷の分と負電荷の分のエネルギーを足し合わせて次のようになるだろう. 中途半端な方向に向けた時には移動距離は内積で表せるので次のように内積で表して良いことになる. とてもシンプルである.

電位を求める

この電気双極子が周囲に作る電場というのは式で正確に表すだけならそれほど難しくもない.それぞれの電荷が独自に作る電場どうしを重ね合わせてやればいいだけである.

電場ベクトルの和を考えるよりも,電位を使って考えた方が楽であろう.電位は電場のように成分に分けて考えなくていいから,それぞれをただ足し合わせるだけで済む.次のようにコンピュータにグラフを描かせることも簡単である.

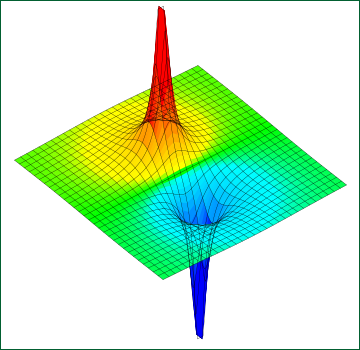
これのどこに不満があるというのだろう？正確さを重視するなら少しも問題がない.しかし我々は二つの電荷の影響の差だけに注目したいのである.差の振る舞いを把握しやすくなるような数式を取り出してみたいと思っている.

次の図のような状況を考えて計算してみよう.

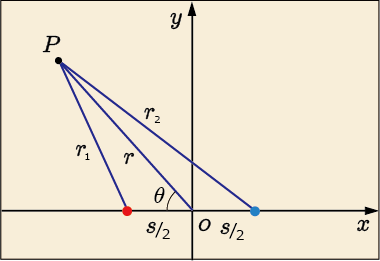
原点を挟んで両側のx軸上に正負の電荷があるような電気双極子から点Pまでの位置関係を説明する図

原点を挟んで両側に正負の電荷があるとしておいた.つまり,電気双極子の中心が原点である.また点 P の座標を (x,y,z) で表し,この位置ベクトルをで表す. 点 P は電気双極子の中心からの相対的な位置を意味することになる.

では進めていこう.それぞれの電荷が単独にある場合の点 P の電位は次のようになる. 合わせると次のようになる. ここで使われている $r_{1}$ や $r_{2}$ は余弦定理を使うことで次のように表せる. これら $r_{1}$ と $r_{2}$ の二つはとても似ていて大部分が打ち消し合うはずなのだが,このままでは計算が厄介なので近似を使うことにする. $x<\!<1$ の時に (1+x)^n ≒ 1+nx が成り立つという公式を使った.今回の場合, $s<\!<r$ だと仮定したのである.電荷間の距離がとても小さく,それを十分に遠くから眺めた場合には問題なく成り立つだろうという式になった. $r_{2}$ についても同様に計算して次の形になる. これらを合わせれば,次のような結果となる.暗算で行けるだろう. ここで使われている cosθ というのはベクトルとベクトルとが成す角のことだから, p・r=qsrcosθ と書ける.つまり, qscosθ=p・r/r なので,これを使って次のような簡単な形にまとめられる. 近似ではあるものの,大変綺麗な形に収まった.図で表現すると次のようになる.

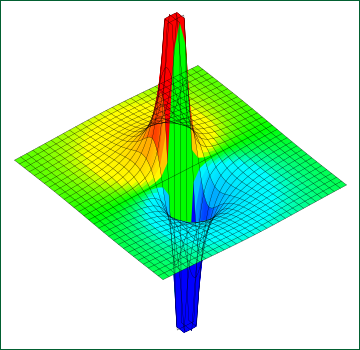
原点のところが断崖絶壁になっており,使用したグラフソフトはこれを一つの垂直な平面とみなし,高さによる色の塗り分けがうまく出来ずに一面緑になってしまっている.

この図は近似を使った結果なので原点付近の振る舞いは近似前とは大きな違いがある.しかしもう少し範囲を広げて描いてやると,十分な遠方ではほとんど差がないことが分かるだろう.

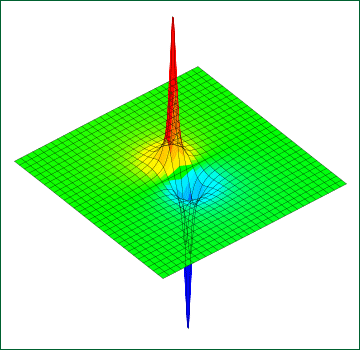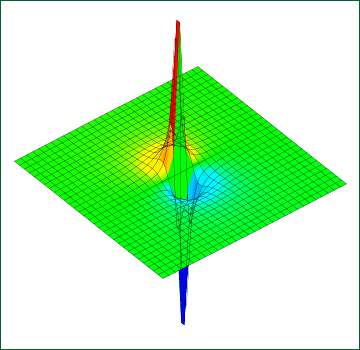
電気双極子の周囲の電位について、近似式を使った場合とそうでない場合のCG画像の比較アニメーション

電場を求める

上で求めた電位を微分してやれば電場が求まる.次のような関係が成り立っているのだった. ベクトルで微分するという行為に慣れていない人もいるかも知れないが,この式は次の意味の計算をせよと言っているに過ぎない. この計算のために先ほどの U(r) を次のように書き換えて表現しておこう. この関数を,,でそれぞれ偏微分しろということなら特に難しいことはないだろう.例えばで偏微分してみると次のようになる. やで微分した場合も同じパターンなので,次のようになる. ベクトルを使えばこれら三通りの結果を次のようにまとめて表せる. 第2項の分母の r^5 が目立っているが,分子にもが二つあるので,実質 r^3 に反比例している.第1項も第2項も r^3 に反比例する形だ.電場の強さは距離の 3 乗に反比例していると言える.次のように書いた方が状況が分かりやすいだろうか. 第1項はの方向を向いた成分で,第2項はの方向を向いた成分である.どちらもに比例する.第2項はの向きによって変化するだけであり,の大きさには関係がない.双極子ベクトルの横の方では第2項の寄与は弱くなる.言葉だけではうまく言い表せないので式を見て考えてみてほしい.

とにかく,距離の 3 乗で電場は弱くなる.単独の電荷では距離の 2 乗で弱くなるが,それよりも急速に弱まる.驚くほどの差がなくて少々がっかりではあるがバカにも出来ない.距離が10倍離れれば,単独の電荷では100分の1になるところが,電気双極子の電場は1000分の1になっているのである.10倍の差が付く.距離が離れるほど両者の比は大きくなってゆくので,大きな違いがあるとも言えるだろう.