電磁波のエネルギー（前編）

エネルギーと運動量

これから電磁波が「エネルギー」と「運動量」を持つことを説明しよう思うのだが,まず簡単な方から済ませたい.どちらも少々面倒ではあるが,おそらくエネルギーの説明の方が楽だろう.

本当はひとまとめにさらっと説明したかったのだが,書いている内に分量が多くなってしまったので,仕方なく二つに分けることにする.前半と後半では内容が大きく異なるので丁度良かったのかも知れない.前半では静電場のエネルギーを求め,後半で電磁波のエネルギーを求めることになるだろう.しかし,飽くまでも前半は後半のための準備作業である,という流れを見失わないために,敢えて題名は変えずに前編,後編としておいた.

電荷が「在る」ことによるエネルギー

電荷はそこに在るだけでエネルギーを持つ,という話を初めて聞くと奇妙な気がするかも知れない.しかし本当なのだ.これからそれを説明しよう.論理的には正しいがちょっと騙されたように感じるかも知れない.

見渡す限り何も無い宇宙の中に半径の金属球が浮いており,これに電荷が帯電しているとする.なぜ球を考えるかというと,帯電した球には電荷が外側に均等に散らばっており,全電荷が中心の一点に集まっているときと同じ形の電場を外部に作るからである.これはまるで一つの点電荷があるように考えられるのでこれからの議論で大変都合がいいわけだ.

この帯電した金属球に微小な電荷を宇宙の果てから近づけることを考えよう.当然,同種電荷の反発力に逆らって近づけることになる.この時,果たしてどれだけのエネルギーが必要であろうか.

答えは簡単だ.無限遠の電位を 0 としたときの金属球表面の電位は,電場 $E=1/(4πε_{0}) q/r^2$ を積分して, r→∞ で 0 になるように積分定数を 0 と置いてやることで, のように求まるので,これに微小電荷をかけてやればいい. この考え方に慣れないのなら力学の仕事の定義に戻って,電場とを掛けて微小電荷に働く力を求め,これを距離で積分してやっても同じことである.

これが微小電荷を一回だけ運んだときに必要なエネルギーである.ではこれを 0 からまで積分してやれば,金属球に電荷が全く無い状態から電荷がになるまでコツコツと電荷を運び続けた時に必要となるエネルギーが求められるではないか. これが金属球に電荷が存在すること自体のエネルギーである.実は金属が全く帯電していない状態から初めの幾つかの電荷が取り付くまでは電場は対称形にはならないのではあるが,これは無限小の電荷を考えているので初めの幾つかのことなど全く無視できる.だから気にしてはいけない.それより気にすべきは,この式の分母に金属球の半径が入っていることである.電荷を r=0 の一点にまで近づけようとすると無限のエネルギーが必要になるのである.これは困ったことだ.電子などの現在素粒子と考えられている粒子は大きさの無い点として扱われているのではないか.しかし電荷が一点に集中するとエネルギーが無限大になってしまう！

そこで,電子は本当は点ではなくてある程度の広がりを持った存在であり,その時のエネルギーは電子の質量が持つエネルギーに等しいのだ,とする仮説が出されたことがある.電子の質量の原因は電荷のエネルギーだというわけだ.こうして求められる電子の半径を「古典的電子半径」と呼んだりするが,あまり根拠のある話ではなく,ちょっと面白い話として捉えておくのが良いようだ.

ファラデーの思想の実現

とにかくこうして電荷が存在することによるエネルギーを求めることが出来たわけだが,話はここで終わらない.上の考え方ではあたかも電荷が位置エネルギーを持っているような表現であったが,ファラデーは電場というものを電荷の周囲の空間のねじれ（エーテルの歪み）であると解釈しており,このねじれにエネルギーが蓄えられているという「力学的な」イメージで捉えていたのである.

すでに存在する電荷に別の小さな電荷を近付けて一体化するまでの電気力線の形の変化を描いた想像図

そこで上で求めた式をファラデー流に変形してやることを試みよう.ファラデー流を実現するためには,空間の各点の電場で表される何らかの量を作ってやり,その全空間の合計でエネルギーを表すようにするのである.

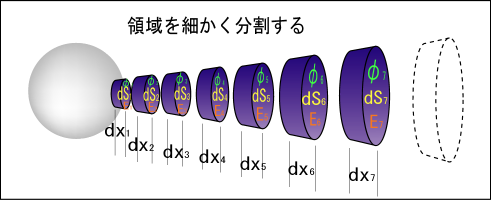
イメージさえしっかり掴んでしまえば高校生でも難しくはないレベルの式変形である.まず,下の図のような円錐形の領域を考える.

この円錐の先頭の部分は金属球の内部にわずかに突っ込んでいる.この金属球から電気力線が出ていると考えて,その束の一部を包み込むように領域を取る.この領域の側面からは電気力線が飛び出していないので,側面に垂直な電場成分は 0 だと言える.このことはこの後,ガウスの法則を使うのに都合がいいのである.

そして,その円錐形を縦に,すなわち電場に垂直に細かく切り刻んで小さな領域に分割してやる.この切り刻んだ幅を $dx_{1}$ , $dx_{2}$ , $dx_{3}$ ,・・・とし,その断面を $dS_{1}$ , $dS_{2}$ , $dS_{3}$ ,・・・とする.そしてその面上での電場を $E_{1}$ , $E_{2}$ , $E_{3}$ ,・・・とし,そのそれぞれの地点での電位を $φ_{1}$ , $φ_{2}$ , $φ_{3}$ ,・・・とする.

これらの記号を使ってもう少し準備させて欲しい.切り刻んだ多数の領域のうち,金属球に頭を突っ込んでいる先頭の部分は,その領域の内部に金属表面の電荷を含んでいる.この領域に含まれる金属表面の面積をとし,金属表面の電荷密度をと置けば,その電荷は w dS と書ける.ここでガウスの法則を使おう.その為に表面の電場を積分する必要があるが,金属内部では電場は 0 であり,側面は電場に垂直なので 0.よって残りは $E_{1} dS_{1}$ だけであり,次の関係が成り立っていることが言える. また,他の区切られた領域についてもガウスの法則を適用すると,これらの内部には電荷を含まないので, という関係が成り立つことが分かる.これらの関係はこの後の式変形の途中で使うことになる.

では式変形を始めるとしよう.先ほどの電荷のエネルギーについての結果を金属球表面の電位を使って書き直すと, と表せる.今,表面の電位は表面上のどの微小電荷についても同じなので,この金属球上の微小電荷 dq=w dS が持つ部分的なエネルギーは, と書いてよい.ここで先ほどの (1) 式の関係を使えば, となる.さらにここでちょっとしたトリックを使い,項の数を増やしてやる. これは前後の項が打ち消しあうようになっており,初めの項以外は勝手に作ったものである.これを展開してやれば, のようになるが,ここで (2) 式の関係を使って, と書き換えてやることが出来る.これはさらに, と変形できるが,この $(φ_{x} - φ_{x+1})/(dx)$ という部分は,を無限小の極限に持っていくことで電場の意味になり,また dS dx の部分も微小領域の体積を表すのでのような意味になる.微小領域を無限に分割した極限を考えれば,この結果は次のような積分で表せる. （この積分範囲は円錐部分のみである.）
電場の強さの 2 乗は,電場ベクトル自身との内積で表せるのでこれを E^2 としておいた.

ここまでは金属球表面上の微小電荷のエネルギーに等しい部分の計算であったが,他の部分も同様に計算できるので,この円錐で全空間を埋め尽くしてやれば,全電荷の持つエネルギーを計算できる. （この積分範囲は空間の全領域である.）
すなわち,各点の電場を計算して全空間で合計してやることで,初めに求めたエネルギーと同じ結果を得ることが出来るというのである.エネルギーは電荷そのものが持っているのではなく,空間に広く分布して存在していると解釈してやることが出来るわけだ.

以上のことから電場が存在する空間のエネルギー密度はのように表せることが分かるのである.