電磁気学：ラングミュア波

プラズマ振動数を導く

前回の話でプラズマ振動数 ω_p というものが出て来た.電磁波がプラズマ中に進入できるかどうかは,電磁波の振動数がこの振動数より高いかどうかで決まるのだった. このはプラズマ中の,電離している電子の密度である.残りの値は,電子の質量や電荷,真空の誘電率など,宇宙が決めた定数みたいなものばかりであるから, ω_p はプラズマの密度だけで決まるものだと言えるだろう.

前回はプラズマ中を通過する電磁波の話だったが,今回は違う.このプラズマ振動数にはそれ以外の意味があることを話したい.これはプラズマそのものが振動する固有振動数でもあるのだ.

この話を後回しにしておいたのは,前回の話を理解する上でかえって邪魔になるかも知れないと思ったからである.プラズマ自体が固有振動を持つことと,電磁波が進入できないこととは直接の関係はない.ないだろうか・・・？なかったよね？

プラズマ振動数は,次のようにイメージすれば簡単に導くことができる.

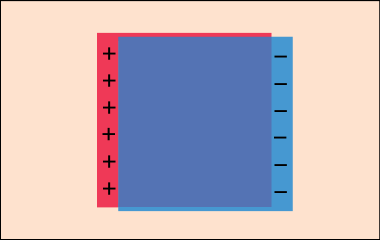
プラズマ中の四角い微小領域を考える.この領域内の電子だけが一斉に左右に振動することを考えよう.もし右に移動したならば,右の端では電子が過剰にあることになり,逆に左の端では電子が少なくなる.元々は電子のマイナスの電荷とイオンのプラスの電荷の量は釣り合って中和していたのだが,このようなズレによってこの領域に電場が生じるだろう.平行平板コンデンサーの極板間に生じる電場と同じ考えで計算できる. このというのはこの領域の側面の面積である.電子の集団が右にだけずれたのだとすると,体積の分の電子が右に押し出されたことになる.電子の密度がだとすると,右に過剰に現れた電荷量は Q=enSx である.よって,電場の大きさは次のようになるだろう. ずれて移動した距離が正の方向だとすると,電場も正の方向に向かって生じるから,負の電荷を持った電子は負の方向へ押し戻されるだろう.これで電子の運動方程式を立ててやる. これを解くと, であり,プラズマ振動数 ω_p で振動することが分かる.これはプラズマ内部の電子密度の変化の振動である.プラズマはどの部分であっても,このような振動数で振動しようとする傾向があるわけだ.

もう少しエレガントに

この計算では四角い微小領域が揺れると考えたり,それが一つの方向にだけ揺れると考えたり,平行平板コンデンサーのような電場が発生すると考えたり,かなり不自然なイメージを取り入れている.現実にはそのような都合の良いことは起きていないだろう.

そういう不自然さを感じさせないようなもっと厳密な計算方法は幾つかあり,それでも同じ結果を導くことができる.しかし最初からそちらで教えられても意味がつかみにくかったりするし,慣れないと難しい.それでも本質的にはあまり変わらないのである.

ここまで言われたら気になるだろうからエレガントだと思う計算例を一つ書いておこう.

電子の密度が時間と場所によって変化するものだとして n(x,t) としておこう.また,電子の集団としての平均速度を v(x,t) としておこう.すると,粒子数の保存則により,次の関係が成り立っている. 電子密度 n(x,t) を,「変動する要素」と「変動しない要素」に分けて考えることにしよう.平均の密度を $n_{0}$ と表し,微小な変動要素を $n_{1}(x,t)$ と表すと,電子密度は次のように表せる. これを (3) 式に代入すると, $n_{0}$ は時間的にも空間的にも変動していないので消せる.消せない部分もあるが,次のように近似してしまおう. なぜこのように近似できるのかを説明し始めるとちっともエレガントではなくなるのだが念のため説明しておこう.本当は速度も,平均の速度と微小な変動部分に分けて $v=v_{0}+v_{1}$ のように表したいのである.しかし平均の速度 $v_{0}$ は 0 でいてくれないと電子は全体としてどこかへ流れて行ってしまうことになる.というわけで,上の式でと表しているのは実は $v_{1}$ の意味なのである.それで, $n_{0}$ との積は 1 次の微小変動量と見なして残し, $n_{1}$ との積はそれよりさらに小さな 2 次の変動量だと見なして捨てたのである.

この式をさらにで偏微分して次の形にしておく. この右辺に ∂v/∂t というものが現れたが,そう言えば電子の運動方程式は次のように表せるのだった. ここにもが出てくる.この式のを (4) 式に代入すれば次のようになる. この右辺の $\nabla・E$ はガウスの法則を思い出させる.ガウスの法則の右辺の電荷密度の部分にはイオンの正電荷と電子の負電荷の密度の合計を代入することになるが,イオンの電荷密度は $en_{0}$ であるから,打ち消し合って残るのは $en_{1}$ である. これを (5) 式に代入すれば次のようになる. これは (2) 式と同じ形の方程式である. $n_{0}$ というのは (2) 式で使っていると同じ意味だから全く同じ解が出てくる.先ほどは電子の集団としての変位が波打つイメージだったが,今回は電荷密度の平均からのズレである $n_{1}$ が波打つイメージになっており,現象を別の視点で眺めることができる.

疑問

しかしこの結果にはよく分からない部分がある.振動数を求めることはできたが,具体的にはどうやって揺らしてやればいいのだろう？外部からこの振動数 ω_p と同じ変動電場をプラズマ全体に掛けてやれば,そりゃあ良く揺れることだろう.しかし当たり前すぎてあまり面白くもない.

いや,ちょっと待てよ？そんなことは可能だろうか？外部から激しく振動する電場を掛けてやるということは,電磁波を浴びせるのと同じであろう.電磁波には波長があるから,プラズマ全体が一斉に同じ動きをするように揺らしてやるなんてことにはならない.

また,この振動数 ω_p 以外の振動数で無理やり揺すってやったらどんな揺れ方をするのだろうとか,そういうことにも興味が出てくる.しかしそれは前回の話と何が違うというのだろう？ ω_p 以下の振動数の電磁波を当ててやっても,電磁波は内部へは入って行けないのだった.その場合,プラズマの表面近くを揺することにしかならないのではないか？

もしプラズマの表面近くの電子を揺すってやったとして,それが内部にまで波のように伝わって行くだろうか？先ほどの計算で求めたのはまだ振動数だけである.もしその振動が波としてプラズマ中の各部に伝わるとしたら,その波長や速度はどれくらいになるだろう？それを知るためのヒントがまだ出て来ていない.

もしプラズマの全体で電子が同じように動くなら,それは波長が無限に長いということになる.それは波なんてものではない.そういう動きではなく,それぞれの場所ごとに違ったタイミングで動くのだとしたら,動き方の違う隣の領域と押し合ったりして圧力を受けることになるだろう.それが考慮されていないのではないか？おそらく,先ほど計算したのとは違ったタイミングで揺れることになりそうだ.

ラングミュア波の導出

プラズマの各部分がそれぞれに異なる動きをした時に感じるであろう圧力まで考慮した運動方程式を立ててみよう.圧力というのは電子の集団に対して働くものだから,今回は 1 個の電子の運動方程式ではなく,微小な領域内にある電子全体の運動方程式にする必要がありそうだ.

直方体の微小領域をイメージして,その微小体積が dV= dS dL と表せると考えてみよう.この微小領域を左から押す力 p(x) dS と右から押す力 p(x+ dL) dS との差がこの領域を押し返そうとする力になる. 微小領域内の全ての電子の質量は nm dV であり,全電荷は en dV と表せるから方程式は次のようになるだろう. 両辺をで割ってやればすっきりする. 電場についてはすでにやった計算と同じなので問題ない.しかし圧力が場所によってどういう変化があるかについてはまだ分からない.熱力学では $pV=Nk_{B}T$ という式があったのだった.は温度, $k_{B}$ はボルツマン定数である.この式の中のは体積中に含まれる粒子数のことである.この両辺をで割ると $p=(N/V)k_{B}T$ であり,この N/V が粒子密度であるから,次のように表せる. この式の中にはが含まれていることだし,は位置によってゆらぎのある量だと考えてやることにして (7) 式に代入して微分してやればいいだろうか？いや,それは正しくない.この式は定常状態で成り立つものなので,平均値を代入して使えるが,密度が激しく変化する状況で微分して使えるようなものではないのだ.電子が激しく振動する時の密度変化は断熱変化である.熱力学によれば断熱変化の式は次のように表せるのだった. というのは比熱比のことだが,考えるのは後にしよう.は断熱変化の間は一定値になるという意味の定数である.この式のというのは,ある定まった数の粒子が占める体積のことを意味するので,が小さくなるということは気体の密度が上昇するという意味になる.とは逆数の関係にあると考えればこの式は次のように直せるだろう. これを微分してやればいい. こうして,解くべき方程式は次のようになった. ところが困ったことに,左辺はの時間微分で,右辺にはの座標微分があり,これでは変位を求める式なのかを求める式なのか,よく分からなくなってしまっている.これを解決するために,先ほど紹介したエレガントな計算手法を真似ることにしよう.まずはを平均部分 $n_{0}$ と変動部分 $n_{1}$ に分けて意味を明確にしたい.右辺の第 2 項にあるは変動部分だけが意味があるので $n_{1}$ に置き換えて構わないだろう.それ以外のは平均値的な意味での電子密度のことなので $n_{0}$ と表すことにする. これを粒子数の保存則から作った (4) 式に代入すれば,密度変化と「電子群の平均速度」との翻訳作業をしてくれるだろう.と言いたいところだが,(4) 式を作った時とは違って今は方向のみの変位を考えているので,ナブラを使うのは大げさである.変位を 1 次元に限定すると (4) 式は次のようになる. ここに (7) 式を代入してやれば次のようになる. 残るは電場の問題だ.第 2 項の ∂E/∂x の部分は,今は方向のみの変位を考えているのでこの形で書かれているが,意味は $\nabla・E$ と変わらない.(6) 式の右辺と同じものが使える. こうして $n_{1}$ のみに関する偏微分方程式にすることができた.

$n_{1}=Ae^{i(kx-ωt)}$ という波の形の解を仮定して代入すると,波数と角振動数の関係が導かれて,知りたかったことの答えが得られるだろう. これは ω>ω_p であれば波数が正の値であり,波として伝播することが分かる.やはり電子密度の波は実際には ω_p で振動するとは限らないわけだ.

この波は密度変化が伝わる波であるが,同時に電場の変化が伝わる波でもある.しかし電磁波と違うのは,これは縦波だということだ.電場の変化の向きが進行方向を向いている.

プラズマ中にこのような波が存在することは,1929年にラングミュアが実験的に発見している.真空管の中に発生させたプラズマ放電に探針を差し込んで電気信号を読み取り,その位置をずらしてゆくことで,その振動数や波長を測定したのである.それでこの波のことを「ラングミュア波」と呼ぶ.あるいは「電子プラズマ波」と呼ぶこともある.

比熱比の値

比熱比として導入したであるが,これは統計力学によると,気体の自由度に関係していることが分かっている. 例えば単原子分子気体の場合の自由度は 3 である.これは分子が 3 次元の空間を自由に移動できることに関係している.理論的には運動エネルギーが座標の 3 成分にそれぞれ割り振られることから定圧比熱と定積比熱が決まり,そこから比熱比が決まるのである.2 原子以上の分子から成る気体になると,さらに分子の回転や振動にもエネルギーが等分に割り振られるために自由度が増えることになる.

電子は自転をしているがその回転エネルギーは外部から与えられるようなものではないし,動きは単原子分子と同じようなものだろう.ということは電子気体の自由度は 3 だと考えてやれば良さそうなのだが,現実にはそうなっていない.今回のような波の場合には γ=3 だと考えると現実に合うのである.ということは自由度は f=1 だということになってしまう.とても奇妙な話である.

これは電子どうしの衝突がほとんど起きていないと考えると説明が付く.先ほどの計算では方向のみの断熱圧縮を考えたのだった.しかし電子どうしの衝突がほとんどないために,運動エネルギーが方向や方向に分配されることが起こる間もなく断熱過程が進むのである.それで 1 次元のみの自由度の断熱圧縮という考え方が当てはまる結果となっているわけだ.

γ=3 を代入するとラングミュア波の分散関係は次のように書けるだろう. ところで,電子の熱速度 $v_{t}$ というものが次のように定義されている. これは電子の運動エネルギーが気体分子 1 個あたりの平均の熱エネルギー $(3/2)k_{B}T$ と同じになる速度という意味であって,気体の平均速度とはまた違うのであるが,だいたい似たような値なので平均速度の代わりとしても良く使われるのである.これを使えば分散関係はのように表すこともできる.

位相速度の下限

この式を見ると,波数が小さくなるほど,つまり波長が長くなるほど,振動数はプラズマ振動数 ω_p に近付いてゆくことが分かる.これはプラズマの広範囲が一斉に同じような動きをしているような状態であり,それ故に,圧力の影響が無視できるようになるのである.先ほども言ったが,全体が同じように動くので波とは呼べないほどであり,位相速度は無限大に近いものだろう.

念のため,速度の計算もしておこう. 確かにが小さくなるにつれて,根号内の第 1 項の影響が増して行き,波の速度はどこまでも大きくなりそうである.第 2 項が無視できるほどになれば次のように近似できるだろう. 逆にが大きくなるとどうなるだろう.根号内の第 1 項の影響は無視できるほど小さくなり,波の速度は電子の熱速度へと近付いてゆく. それ以下にはならない.この時,振動数と波数の関係は ω≒v_t k になっている.つまり振動数が大きくなるほどその状態に近くなるとも言えるわけだ.

ランダウ減衰

振動数を上げていって,波の速度が電子の熱速度近くまで落ちてくると,波のエネルギーが急激に弱められる現象が起きてくる.これを「ランダウ減衰」と呼ぶ.

先ほど,この波は電場の変化の波でもあると話しただろう.電子の熱運動の速度がこの波の速度に近いということは,電子が走るのに合わせて電場がいつまでもついてくるということであり,電子は電場から連続的な加速を受けることができるようになる.波の速度よりわずかに遅い電子は波からエネルギーを吸収して加速し,波の電場はエネルギーを奪われて,弱められるというわけだ.

逆に,波よりわずかに速い電子は減速されて,波にエネルギーを与えようとするのだが,電子の速度分布から考えて,速い電子よりも遅い電子の方が数で勝っているのでこのような減衰が起こるのである.

この現象をきっちり説明するには電子の熱運動の速度分布を取り入れた数式が必要になる.それは粒子の集団についての方程式で,「運動論的方程式」と呼ばれるものである.それとプラズマ内の電場の式を組み合わせたワンセットで「ブラソフ方程式」と呼ばれるものになるが,それを解かなければならない.

そこまで説明するには解析力学や統計力学の知識を援用する必要があるので,今回は見送った.今回の説明ですら熱力学の知識を幾つか借りて来ており,「電磁気学」の範囲で行う説明としてはギリギリである.今回の計算結果は,その方程式の近似として得られるものに過ぎない.

プラズマの専門書では,いきなりこの「ブラソフ方程式」を使って説明しているか,あるいはもっと簡単そうに見えるものであってもそのやり方に強く影響を受けたやり方で書かれているものが多いので,非常に分かりにくかったりするのである.