この解説の目的
ここでは直線状に一様に分布する電荷が周囲に作り出す電場を計算する.この結果は直線電流が周囲に作る磁場と良く似た形になるので,ビオ・サバールの法則を導き出す部分のヒントになるだろう.
計算結果は目的ではない.答えを知りたいだけならば「ガウスの法則」を使った方が簡単に求められる.そのやり方が分からない人は,ここでは説明しないので他の教科書で勉強してほしい.
ここでは基本に返って,理解しやすい代わりに計算には少し手間の掛かる方法をわざわざ選ぶことにする.
まず,軸上に一様な線密度
で電荷が分布しているとしよう.微小長さ
内に存在する電荷は
だという考えである.このような電荷が
から
に至るまで途切れることなく存在しているとする.
電場の強さは軸からの距離
のみで決まり,
軸に垂直な方向を向いているに違いない.なぜなら,電場を測るために
軸に平行にどれだけ移動してみても状況は何も変化せず,
軸の正負のどちらの方向を眺めてみても対称に分布があるからである.電場がどちらかに傾いて存在する理由が見出せない.
説明しやすいように,原点から軸に垂直な方向に距離
だけ離れた点を A として,点 A での電場を計算するとしよう.点 A の電場に影響を与えるのは
軸上のあらゆる点にある電荷であって,それらの影響を全て足し合わせないといけない.
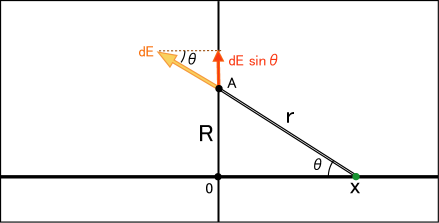
例えば,原点から軸方向へ
だけ離れた点の近くの微小長さ
内にある電荷は
であり,この電荷はほぼ一点にあるとみなせるだろう.ここから点 A までの距離は
である.よって,この微小な電荷が点 A に作る電場の強さ
は,
と計算できる事になる.しかしこれは
軸に垂直な成分の値ではない.
軸に垂直でない成分は原点を挟んで反対側の電荷の影響と打ち消しあって消えてしまうのである.よって,初めから
軸に垂直な成分だけを表して積分しておけば手間が省けるだろう.先ほどの式に
をかけておけばいい.この
というのは,電荷の位置から点 A を見たときの
軸との角度である.
あとはこれを軸の
から
まで積分してやればいいのである.
ところが,この式の中にある
も
の関数ではないか!このままでは計算できない.
と
との間にどんな関係があるかと言えば,
であるが,これを代入してみてもどうも簡単には積分できないようである.それなら逆に,
であることを使って,
の方を
で表してみたらどうだろうか.
これらを代入してやって,
で積分してやる.
こうしてめでたく結果を得る事が出来た.しかし最後の方の計算テクニックはどうでも良い.一番大切な部分は,この結果が各点からの
という寄与を積分することで得られるのだという点である.










