電磁気学：物質中の光速

単純な理屈は役立たず

光が水やガラスに差し込む時には屈折が起きる.これは物質中での光の速度が,真空中よりも遅くなると考えれば説明が付く.このことは高校物理でも学ぶので省略しよう.

真空中での光速は誘電率 $ε_{0}$ や透磁率 $μ_{0}$ を使ってのように表すことができたのだった.物質中では誘電率や透磁率の値が真空中とは異なるのだから,それらを使って同じ形で表してやれば,光が物質中で遅くなる現象についても説明がつくのではないだろうか.

ところがそれが上手くは行かないのである.光が遅くなることは説明できても,数値がかなり合わないのだ.試しに少し計算してみようか.

水の屈折率はおよそ 1.3 であり,これは光が真空中より約 1.3 倍遅いということである.水の比誘電率は温度によって変わるが 20℃ で 80.4 である.比透磁率はとても大きな値を持つ物質もあるが,ほとんどの物質でおよそ 1 であり,水もそうである.比誘電率や比透磁率というのは真空の誘電率や透磁率と比べた場合の倍率のことなので計算がとても楽である.つまり,こういうことだ. 水中の光速は真空と比べて 9 倍も遅いということになる.いや,ちょっと待て.屈折率がおよそ 9 だなんて物質は聞いたこともないぞ！1.3 には程遠い値だ.

それだけではない.これではプリズムを通った光が七色に分かれる現象の説明もできないのだ.この現象は光の波長ごとにガラスの屈折率が異なるために起こるものだと考えられる.つまり,物質中での光の速さは波長によって微妙に異なっているはずなのである.どのように考えたらそのような内容を説明することができるのだろうか？

電子の動きを考慮する

誘電率や透磁率というのは,もともとは静電場や静磁場を想定して考え出されたものだった.しかし光というのは電場や磁場が高速で変動しながら伝わるものなので,想定外のことが起きているに違いない.電場や磁場の振動数によって値が変わるようなものだと考えた方が良さそうだ.

物質中で電磁波の影響を強く受けるものと言えば,電子だろう.電子の動きを考慮に入れたマクスウェル方程式を作る必要がある.そこでまずは,物質中の電子が電磁波を受けたときの運動方程式を作ってみることにしよう.電子が相対論的な速度ではないと仮定すれば,電磁波の磁場成分から受ける力を無視することができて簡単だ.また,電子は原子に束縛されており,定位置から移動するとバネのような復元力が働くと仮定する. ここでというのは電子の電荷であり e<0 である.電磁波の電場成分は $E=E_{0}cosωt$ と表せる形であるとしてみた.上に書いた運動方程式は 1 次元のみで考えているが,別に問題ないだろう.

さて,現実に電子にバネが付いているわけでもあるまい.バネ定数を使うより,電子の固有角振動数 $ω_{0}$ を使って表した方が現実的だ.我々はバネに繋がれた質点の問題は力学でよく知っていて,バネ定数がであるときの角振動数はであるから,次のように書き換えることができる. では,この微分方程式を解くという問題が我々の手に負えるものかどうか,しばし眺めて考えることにしよう.・・・・・・.おお！これは「定数係数線形非同次微分方程式」ではないか！次のように整理すればそれであることがよく分かる. これを解くのはそれほど簡単だとは言えないが,お決まりの手順で解くことができるという意味では簡単である.力学に出てくる強制振動と同じ内容なので,力学の教科書には簡略化した考え方での解き方が載っていたりもする.解き方は数学の問題なのでここではやらない.解は次のようになる. 最初の二つの項が一般解と呼ばれるもので,最後の項が特異解と呼ばれるものである.

一般解の方は sin と cos の自由な組み合わせになっていて,三角関数の合成の公式を思い出してもらえば分かるように,位相のずれもこれで表現できる.要するに,次のように書き換えることもできるだろうということだ. 一般解の方は電磁波の影響とはまるで関係のない,位相も振幅も気ままな熱運動的な揺れを意味する.一方,特異解の方は外部から来る電磁波に同期したような揺れ方であり,振幅も電磁波の強さによって決まってしまう.現実にはその二種類の振動を重ね合わせたような少し複雑な揺れ方をするというわけだ.

熱運動的な乱雑な動きは多分,全体としては平均化されてしまって,電磁波に影響を与えないことだろう.今の話で興味が有るのは電磁波によって物質内に引き起こされる現象であるから,そちらの振動成分の方だけを取り出して,その振動成分によって起こる現象を見ていくことにしよう.以後は特異解の方だけ取り出して,電子の動きを次の式で考えることにする. これを微分することで電子の速度が計算できる. 電子が運動すれば電流になる.電子の密度を使えば,電流密度は i=eNv で表される.その方向は電場の向きと同じ軸上であるから,そろそろ次の計算に備えてベクトルで表しておこう. これは一定方向に流れ続けるようなイメージの電流ではなく,電磁波に合わせて細かく振動するような電子の動きである.物質内に引き起こされるこの電子のさざ波のようなものの強さが,外部からやってきた電磁波の振動数によって異なっていることが分かるだろう.これが物質中の光速の違いに影響するのだな,と予感される.

さて,真空中でのマクスウェル方程式の一つに次のようなものがあった.「アンペール・マクスウェルの法則」である. 今は物質中でのことを考えているわけだが,物質中の電子の影響さえなければ真空と同じようなものだろうと考えてこの式を使う.つまり今回の話は,真空での現象に電子の影響が加わっただけであるという視点である.この式の電流密度のところに先ほどの結果を代入する.また $B=μ_{0}H$ や $D=ε_{0}E$ という関係も使う. このというのは今は電子を揺さぶっている電場のことだから $E=E_{0}cosωt$ である.これを代入して整理してやると次のようになる. さて,この式の中の $ε_{0}μ_{0}$ が気になる.これは真空中での光速に関係している部分だ.もし電流密度が存在しない真空中であれば,この式は次のようになっていたはずである. マクスウェル方程式を物質中に適用するときに,今回のように物質中に生じる電流密度のことなどわざわざ意識することなく使えるのなら便利であろうなぁ,と思う.誘電率や透磁率を物質中での値に書き換えるだけで,真空中の場合と同じように考えられるようにしてみたい.今回導いた (2) 式も,(3) 式と同じように次のような形に表せるようにしたいのである. それは,次のような関係が成り立っているのだと考えることにすれば実現できる. 物質の誘電率や透磁率は電磁波の振動数によって値が変化する量だと考えることにするのである.これを使うことで物質中の電磁波の速度を次のように表すことができる. なるほど,真空中の光速より遅くなるように見えることも,振動数によって光速が変化することも表されている.いや, $ω_{0}<ω$ の場合にはかえって光速よりも速くなりそうだな・・・？本当にそのようなことが起きるのだろうか？この計算結果は実験値にどれくらい近いと言えるのだろう？

それを確かめる前に,式が少しややこしい感じに見えるのを何とかしておこう.屈折率で表しておいた方が少しは簡単に見えそうだ. もしも読者がプラズマについていくらか学んだことがあれば,もう少し簡単な式で表すこともできる.プラズマの性質を表す基本的な量である「プラズマ振動数」というものがあり,それは次の式で表される. これを使えば,次のようにすっきり書けるだろう. しかし ω_p は今回の話にはあまり関係してこないので,電子密度によって決定されるただの定数だと思っていればいいだろう.

実際の現象と一致するか

この結果をグラフにすると次のようになる.

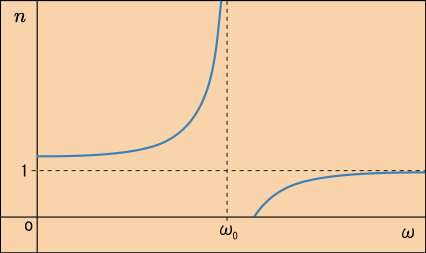
ここでは大げさに表現してあるので振動数が 0 になるところで屈折率が 1 より大きくなっているが, $ω_p <\!<ω_{0}$ ならほとんど 1 になるだろう.つまり,電磁波の振動数が大きくても小さくても屈折率は 1 へと近付くということらしい.そして固有振動数 $ω_{0}$ に近付くほど,屈折率は 1 からどんどん離れて行くようだ.

ちょうど固有振動と同じになるところでは屈折率が無限大になっているので,どんなすごいことが起こるのだろうかと気になるわけだが,ここまで計算した内容の意味を考えれば大体想像できる.電子がちょうど揺れやすいタイミングで揺さぶられるので,揺れの振幅は非常に大きくなるわけだ.しかし無限に激しく揺れて,ついには物質が崩壊したりするわけでもないだろう.それは熱振動と同じような揺れなので,電磁波が電子を揺らしたエネルギーは熱エネルギーとなって周囲に拡散するに違いない.屈折率が負の無限大になることもないだろう.電子が無限大の振幅で揺れるなんてことは起こり得ず,実際は次のようになまった形のグラフになるはずだ.

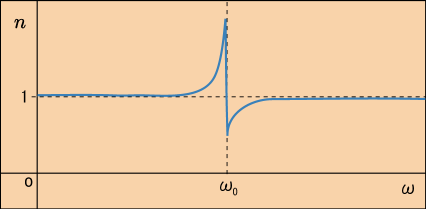
屈折率の理論上のグラフから無限大への発散を取り除いて現実に合わせた形に書き直した図

先ほどは大げさに描きすぎたのでちょっと反省してスケールを変えてある.これでも大げさ過ぎるかも知れない.

しかし,本当にこんなことが起きているのだろうか.試しに水の屈折率のデータを探してみたが,この式の形が正しいという確信は得られなかった.グラフにしてみるとかなり直線に近くなってしまうのである.可視光線というのは電磁波の中ではごくごく狭い範囲の振動数に過ぎないのだ.

20℃の水の屈折率（ネットのあちこちで拾ったデータ）
波長 [nm]	振動数 [×10¹⁴Hz]	屈折率
656.3（赤）	4.568	1.3311
589.3（橙）（ナトリウムD線）	5.087	1.3330
546.1（黄緑）	5.490	1.3345
405（紫）	7.40	1.343

水の場合,屈折率が 1 よりも大きくて振動数が上がるほど屈折率が大きくなることから, $ω_{0}$ は可視光の領域よりも高いところにあるのだろう.しかしその値が幾つくらいであるのかを正確に導くのは無理がありそうだ.

水の場合にはたまたま $ω_{0}$ が可視光の振動数より高いのだが,物質によっては可視光よりも低いところにある場合もあるだろう.そういう物質の可視光領域での屈折率は 1 より小さくなったりもするようだ.上のグラフの示す通りである.しかしどちらであろうと赤い光の方が屈折率が低く,青い光の方が屈折率が高いという点は変わらない.こういうものは「正常分散」と呼ばれる.

ところが $ω_{0}$ がちょうど可視光の範囲内に位置するような物質もあるそうだ.そのような物質でプリズムを作ると,七色の光が見慣れた順序では並ばなくなるそうである.そのような屈折の仕方をするものを「異常分散」と呼ぶ.どういう並びになって見えるかはクイズにしようと思ったが,自分も気になったので図にしてみた.まったくのイメージ図であって,角度などは正確ではない.

七色の光がプリズムで分かれる様子を描いた図。正常分散の場合と異常分散の場合を並べて表示

左が正常分散の例である.ここでは屈折率が 1 より大きい場合を描いてみた.そして右が異常分散の例である.ここでは $ω_{0}$ がちょうど緑色の領域に一致する場合を描いてみた.つまり,緑の光より高い振動数の光の屈折率が 1 より小さくなっている.緑の光は媒質に吸収されるため,両脇にかすかに見えるが,暗くなっている.中央付近が暗いのは紫外線や赤外線であり,人間の目では見えないから黒く見えるのである.

砂川重信著『理論電磁気学』(p.207)によれば,フクシンという染料物質のアルコール溶液で作ったプリズムがこのような性質を示すそうである.フクシンの溶液が紅紫色なのは,緑色の光を吸収するために,その補色が目に見えているのだろう.

そういう物質が実際にあるとは驚きだ.ということは,ここまで考えてきたイメージはかなり現実に近いということになるだろうか？

何かがおかしい

しかしまだ納得の行かない点がある.このグラフでは電磁波の振動数をどんどん小さくして行ったときに屈折率が 1 に近付くことになっている.これは本当だろうか？

冒頭で試した計算では,静電場に対する水の屈折率は約 9 になるのだった.いや,静電場は電磁波とは違うものだから屈折率などという考えはおかしいのか・・・.静電場は電磁波のように移動していくようなイメージのものではないからそもそも屈折なんてしない.

では屈折率で考えるのをやめて,誘電率で考えることにしよう.透磁率は無視することにする.なぜなら,水は強い磁性を持たないので,比透磁率はほとんど 1 だからである.どんな振動数の電磁波に対してもそれは変わらないだろう.そういうわけで (5) 式のように表された屈折率の変化はほとんどが誘電率の変化によるものだと考えられる.(5) 式を見るよりも (4) 式に $μ/μ_{0} ≒ 1$ を代入して変形した方が楽か. これが比誘電率を表す式だということになる.水の場合,静電場に対しては比誘電率が約 80 になるという実験結果が出ているのに,この式ではそのようにはなっていないのが気に入らない.上で行った計算では何か重要な要素が欠けているのだろうか.電子の振る舞いについての先ほどのイメージは何か間違っているのだろうか？

あるいは,静電場と電磁波では全く別の扱いをするべきなのかも知れない.静電場用の誘電率と,電磁波用の誘電率とを使い分けるべきなのか・・・？しかしよく分からない.静電場がごくごくゆっくりにでも変動すれば,それは電磁波と呼べるだろうか？ゆっくり変動する静電場があれば,それは静電場と電磁波の重ね合わせだと考えることもできそうだ. ω→0 で静電場の誘電率と一致しなければならないとは言えないのかも知れない.

それでも気になるので,証拠を求めて,可視光の範囲を遥かに外れたところでのデータを探してみた.低周波の電磁波に対する屈折率の資料が欲しかったのである.それは「The optics of a water drop」という海外サイトの一部である次のページに見つかった.

Refractive index of water

そこの Fig.7 というグラフがそれである.横軸が波長で,対数表示になっており,右へ行くほど振動数が小さいことに注意が必要だ.驚いたことに,このグラフは (5) 式の振る舞いとはまるで違っているではないか.合っているように見えるのは可視光の近くのごく狭い範囲,つまり 100nm - 1μm の目盛りの右半分ほどだけだ.

ところが,このグラフによれば, ω→0 で約 9 へと向かっているのである.やはり静電場の誘電率と電磁波に対する誘電率は滑らかに繋がるべきものなのか.先ほどの考えを変更する必要がある.

誘電率の意味

そもそも誘電率とは何であったか？物質に電場が掛けられた時に,内部の正電荷と負電荷がズレを起こす.これを分極と呼ぶのだった.元々はそれらの電荷は釣り合って全体としては中性のように振舞っていたのだが,分極のために新たな電場が生じる.その電場と外部の電場は向きが逆であって弱め合い,結果として物質内部では電場が弱くなるのである.その弱まる度合いを表すのが誘電率である.しかし「真空の誘電率」にはそのような意味は無い.真空の誘電率は理論上の都合で係数の調整役を引き受けさせられているのであり,真空の誘電率を 1 だとするような理論の組み方もやろうと思えばできるのだった.

そういうわけで,我々に分かりやすいのは誘電率を真空の誘電率で割った値である「比誘電率」というものである.もし比誘電率が約 80 だというなら物質内部の電場は約 1/80 に弱められていることを意味する.

さて,電磁波の場合も似たようなことが起きていそうなのだが,本当にそう言えるだろうか？電磁波の電場に合わせて電子が元の位置から移動すれば,これは分極が起きているのと同じ効果がありそうだ.物質内部に侵入する電場を弱める働きがあるだろう.いやいや,待てよ？そうだとも限らないのか.電磁波が固有振動数 $ω_{0}$ よりも速く振動する場合にはなぜか電子の動きが電磁波のタイミングとは逆転してしまって,かえって内部の電場を強める効果が起きてしまうことになる.それについてはプラズマ中を電磁波が通過するときに起こるのと同じであり,それほど悩むものでもない.

しかし数量的にはどうなのだろう？ここに来て,誘電率の物理的意味が,静電場の場合と電磁波の場合とで本当に同じだと言えるのかどうかが非常に気になり始めてしまった.先ほどの「アンペール・マクスウェルの法則」の式を使った説明では,電流密度の影響を誘電率の値に無理やりねじ込んだ形になっている.この意味がどうも分かりにくい.比誘電率の値がなら,物質中を進む電磁波の電場は物質に入る前の電磁波の電場の 1/a 倍になっているなんてことは果たして言えるのだろうか？

次のように考えてみよう.物質に進入する前の光線の電場をだとしよう.今後はこれを外部電場と呼ぶことにする.物質内部の電子が移動することによって分極電場 E'' が生じ,それによって打ち消された残りが物質内部の電場として残るのだとすると,次のような関係になっている. ここで,「ラングミュア波」について論じた時のような,電子の集団の変位に比例して分極電場が生じるという単純な考え方を適用するなら,分極電場 E'' は次のように表せるだろう. マイナスを付けてあるのは,この分極電場が外部電場を打ち消すような向きに働いていることを考えてのことである.（ラングミュア波の記事中の式では電場の強さだけを問題にしていたのでマイナスを付けていなかった.）こののところに (1) 式を代入してやれば次のようになる. これを (7) 式に代入してやろう.また (7) 式の右辺には $E=E_{0}cosωt$ を代入してやることにしよう.これは最初の計算の仮定として使った電場と同じ形である.最初の計算の時にははっきりさせておかなかったが,あの時に仮定した電場というのは,実は物質内部での電場のことを意味していた,ということになるだろうか.なるほど,電子は物質内部の電場に動かされていると考えるのが至極当然である. これを移項することで, という形になり,(6) 式と同じ形の量がここにも姿を表わす.この結果はまさに,内部電場 $E=E_{0}cosωt$ と外部電場との比が,比誘電率によって表わされるという内容になっている.比誘電率の値がなら物質中の電場は物質に入る前の電磁波の電場の 1/a 倍になっていることが言えたのである.この法則が成り立っているということは「フレネルの式」で議論した内容が理論上だけのものでなく,現実の物質についてもそのまま当てはめて使えるという保証になっている.これで一安心だ.

こうして二通りの方法で誘電率の変化を説明することに成功した.「アンペール・マクスウェルの法則」を使って説明しなくても,最初からこのやり方で説明しても良かったのかも知れない.

以前,プラズマ中の電磁波を説明した時に,プラズマ中の電磁波の電場が理論上は容易に無限大になってしまうので,そんなことは現実には有り得ないと一蹴したことがある.ところが,今の考え方を適用すると,確かにプラズマ中の電磁波の電場は外部電場よりも増強されているのであり,比誘電率の値が内部電場と外部電場の比を表しているという法則は比誘電率が 1 より小さい場合であっても成り立たねばならないことになりそうだ.増強された内部電場によって分極が起こるので内部電場はさらに増強され,理論上は容易に無限大の電場が実現することになる.しかし現実には電子はそこまで激しく振動することはないので,増強の度合いも頭打ちになるのである.

静電場と電磁波,どちらも分極で説明できるのなら,値が滑らかに繋がっても良さそうなものだが・・・.

分極の仕組みは一つではない

どうやら物質の内部で起こる分極の仕組みは,単純に電子が揺れるようなものだけではないようである.

水の場合,水分子の一つ一つの中に電荷の偏りがあり,外部から電場が加わると分子自体が向きを変えることで分極を引き起こす.これは電荷が大きく移動するため強力であり,水が静電場に対して高い誘電率を示すのはこの仕組みがあるからである.しかし電場の激しい変化にはほとんど付いて行くことが出来ない.付いて行けないと,その分極の仕組みは最初からなかったも同然となる.電磁波の振動数が少し上がっただけで高かった誘電率の値が急激に落ちるのはこのためである.分子そのものの向きが変化することによって起こされるこのような分極は「配向分極」と呼ばれている.

他には「イオン分極」と呼ばれる仕組みもある.これは塩化ナトリウムのようなイオン結晶を構成している中で,正負の電荷を持った個々のイオンがその場で振動することで起こされるものである.これは今回の理論を当てはめることができるが,質量は電子よりも大きい数値を使うことになるし,固有振動数は電子の振動よりもかなり低い.

今回の理論のような状況は,原子の内部で電子がわずかに振動することで現実に起こる.これは「電子分極」と呼ばれている.この分極はあらゆる物質で起こるものである.この振動はかなり高い振動数にまでついて行くことが出来るので振動数を高くして行っても最後まで残るだろう.

これらが組み合わさった結果として,振動数による誘電率の変化,それは屈折率の変化でもあるわけだが,それは次のような曲線を描くことになる.

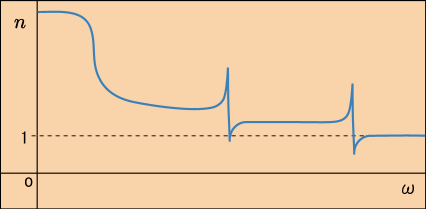
これはかなり誇張した概念図であるが,振動数が高くなるにつれて分極の機構が一つまた一つと働かなくなって行く様子が分かるだろう.

分極の仕組みは今紹介した以外にも物質によって様々であることだし,全ての分子,全ての電子が同じ固有振動数で揺れるわけではないので,実際にはこの概念図よりももっと複雑なことになっていることが予想できる.こうして,先ほど紹介したサイトにあった複雑なグラフの形が定性的には説明できたわけだ.