複雑になっても基本法則は覆らない
要修正:この記事内容は掲示板で議論中であり,解決しない問題が多く含まれています.鵜呑みにしないように気をつけて下さい.
電磁気学の範囲内で運動量保存則が成り立っていることはすでに説明した通りであり,疑いがない.電荷を持った粒子の運動だけを見ていると運動量が失われたように見えることもあるが,実は電磁場も運動量を持っており,そこまで考慮すれば失われていないのであった.
現実に起こる現象というのは理論なんかよりもずっと複雑なものである.既知の法則の組み合わせに過ぎないものが予期せぬ現象を生み出したり,それを理解するために新たな概念が必要になることもあるだろう.確かに,部分を理解すればそのまま全体が理解できるというものではない.それであっても,既知の法則の組み合わせで生じている以上は,すでに確立した法則を覆すことはない.
いや,ないとは言い切れないかな・・・?基礎法則の方に見落としがあるかも知れない.しかし法則が覆るとしたら,基礎となる理論の方にまで変更が必要になるときであろう.
そこまで頭の中では分かっているつもりだとしても,現実の現象を観察していると,時々疑問が生じるときがある.例えばローレンツ力の反作用は一体どこに働いているのだろうか,とか・・・.そんなことはミクロに分解して考えたときには説明済みだと思ったのだが,実際の装置を前にして,どう考えていいか分からない状況というものが起こり得る.
今回のタイトルは人の関心を引くにはいいのだが,あまり正確ではない.ローレンツ力の反作用が一体どこに現れているかさっぱり分からないとき,こんな現象が起こっている可能性もありますよ,という一例を説明したいと思う.
これは反作用のない回転か?
一回ループして輪になった導線に磁石を近付けると,電磁誘導で電場が生じ,電流が流れる.この時の導線内の電子の流れに影響されて導線全体が勢い良く回転を始めるかというと,そうはならないだろう.なぜなら,導線内には電子と同じ量の電荷を持つ陽子が存在していて,それらが電子とは反対向きの力を受けるからである.
しかし代わりに帯電した導線を使えばどうだろうか.円形導線の中心を軸にして回転するように糸でつるしてやればいい.導線全体が回転するような力を受けそうだ.もしそうなるとしても,この反作用はどこに向かうだろう.何かが代わりに逆回りするだろうか?
この話を考えるとき,円形導線の中心軸上に沿って磁石を近付けてゆくことを想定することが肝心だ.そうしなければあまり不思議だとも思えない現象が混じってしまって問題の本質が見えにくくなってしまう.
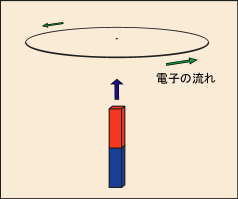
そのような条件の上で,もう一度尋ねよう.反作用の相手としては磁石しかなさそうだが,磁石は反作用で逆回りするだろうか.導線上に電流が生じたせいで磁場が作られ,それによって磁石が退けられるような向きの力は働くだろう.しかし磁石を回転させるような作用はどこからも生じていないように見える.角運動量保存則は一体どうしてしまったというのだろう.
逆に磁石の方を固定して,帯電した円形導線を磁石に近付けても導線だけが回転することになる.この場合は導線内の電荷が磁石に近付くときにローレンツ力で進路が曲がり,電流が生じ,それに押されて導線が回転したという説明になるが,視点が違うだけでどちらでも同じ現象だ.
この現象は磁石を遠ざけるときにも起こる.一旦磁石を近付けた状態で,導線の回転を手で止めてやって,(そのときに帯電した電荷が逃げないように工夫する必要があるが)それから磁石を遠ざけるようにすれば,導線の輪は先ほどとは逆向きに回転するだろう.
静電磁場が角運動量を持つ
答えをさっさと明かしてしまうと,この時に保存されていないように見える角運動量は電磁場に移されたのである.それは電磁波となってどこかへ飛び去ってしまったわけではなく,何と,この装置の近くに静かにとどまっている静電磁場が持っているのである.
以前にポインティングベクトルというものを考えたことがある.それは電場と磁場の外積を計算したもので,それをで割ったものが電磁波のエネルギー密度を表しているのだった.それをさらに
で割れば,電磁波の運動量密度を表しているとも言える.しかしその定義によると,電磁波の場合だけでなく,静電場と静磁場についても同様な計算が出来て,何も動いているものがないのに運動量密度が計算できてしまうという不思議なことになってしまうのだった.それを不審に思った私はそこで「この解釈は電磁波についてだけ成り立つものである」という説明を付け加えたのであった.
ところがそれは正確ではなくて,全く静止しているように見える静電磁場でさえ,その場に「運動量を蓄えている」ことがあるようなのだ.そして同様に,何も運動している実体がないのに静電磁場が角運動量を持つことさえもあるというのである.
ちょっと弁解させてもらうと,初めてポインティングベクトルが出てきたところでは,それを「単位時間に単位面積を通過するエネルギー」だと解釈したので,それは電磁波についてだけの話だと書いたのである.だから,ちょっと視野の狭い説明ではあったかも知れないが,間違っていたわけではないと思うのだ.
このことについて説明している教科書はそれほど多くはないとのことだが,権威付けのために書いておくと,岩波現代文庫の『物理法則はいかにして発見されたか』(ファインマン著)という本の第 3 章,116 ~ 117 ページにこの話が出ている.実は私はそれを見て,この記事を書く気になったのだった.
これはちょっと驚きだった.本当に何も動くものがないのに,角運動量を持つことがあるなんて・・・.そして電子のスピンのことを思い出す.あれは数学的な構造が通常の角運動量に似ているだけであって,何かが実際に回転しているわけではない,という説明を受けたことがある.それでも心のどこかで,ミクロな何かが回転しているイメージを捨て切れないでいたのだった.回転していないものが角運動量を持つなんてことがあるだろうか,そんなものは全く想像できない,と.それが,こうも身近に,量子力学以前の話としてあっただなんて.
家庭内で手軽に実験できるか
とりあえず簡単な実験も試してみたが,うまく行かなかった.夏だから湿気が多くて静電気がほとんど発生しないのである.仮に発生できたとしても帯電させておくことが出来ないだろう.今のところそれが一番の理由である気がするのだが,果たして原因はそれだけだろうか.そもそも家庭内で試せるほどの効果が出るような現象なのだろうか.
今,ざっと計算してみたが,家庭内で手軽に検出するのは無理だという結果になった.参考までに計算内容を書いてみるか.
まず,磁石の磁束密度ををだとする.ちょっと強め.磁石の断面積を
だとすると,磁束は
ウェーバーってとこか.これを 1 回巻きコイルに 1 秒かけて近付けるとすると,
程度の起電力が発生する.うーん,かなり少ないなぁ.見積もりを間違ってないだろうか.まぁ,電磁誘導の実験にしても 100 回巻きコイルとかを使って,もっとずっと素早く動かして,豆球をやっと灯せる程度だから,そんなものでしかないのかな.
コイルの半径をくらいだとすると,円周の長さで割れば電場の強さが出る.
.それに電気素量をかければ,電子 1 個あたりに働く力の大きさが計算できる.これが
ニュートン.力のモーメントはこれにコイルの半径をかけて,
.かなり小さくなってきた.この時点で期待薄だな.
力のモーメントというのは角運動量の時間変化率として表せる.今,1 秒をかけて磁石を近付ける場合を考えているので,かなり大雑把な計算ではあるが,簡単のために力のモーメントがずっと一定だと仮定してやって,角運動量の値を力のモーメントと同じだとしよう.これは電子 1 個あたりの角運動量なので,一体何個の電子がこの現象に関与してくれるかで全角運動量が決まるわけだ.そう言われてみれば,下敷きの摩擦で発生するような,体に感じる程度の静電気っていうのは,一体,何個くらいの電子が関与している現象なのだろう?身近なことなのにあまり考えたことがなかったな.
ちょっと検索してみると,体に衝撃を感じるほどの静電気の量として,およそ「 クーロン」という数値を見つけた.これは人体にたまる全体量だろうからかなり多い値になっているだろうが,とりあえず電子数に換算すると
個くらいだろうか.それでもかなり少ないな.
別の方法でも見積もってみよう.無限の広さの平板に電荷密度で一様に分布しているとき,電場は
となるというのは電磁気学の練習問題でよく出てくる話だ.空気中で静電気が放電するとき,約
あたりで
くらいの電位差があると聞くので,電場は
くらいが限界であろう.それ以上強いと,空気の絶縁を破って放電してしまうということを意味するからだ.ここから電荷密度
を逆算すれば,
といったところか.
あたりに直せば,電子が
個程度ということになる.やはりそんなものか.
すると全体では角運動量は程度.これで導線はどれくらい回るか.大サービスで導線の重量を 1 g 程度と小さめに見積もろう.慣性モーメントは,
となるから,角速度
は
を使って,
.これを
で割れば 1 秒あたりの回転数が出るが,計算する必要もないだろう.小さすぎて検出不能だ.
なるほど,道理で,この現象をわざわざ紹介している教科書が少ないわけだ.
計算法を工夫してみる
これからやろうとしているのは,上で話した内容を単純な方法で計算して確かめることが出来ないか,という試みの紹介である.つまり,角運動量の変化を,ちゃんとポインティングベクトルによって説明できるのかどうかということの確認だ.徹底的に部分に分割する方法で厳密に証明しようとするなら,それは第 2 部で行った説明,つまり電磁場が運動量を持つことを示した計算ですでに十分だろうと思うのだ.しかしここでは,なるべく直観的に納得できるような別の形でやってみたいのである.
輪になった導線上に分布する電荷の作る電場というのは,結構面倒な形をしている.磁石の作る磁場というのも面倒だ.それらの外積を場所ごとに計算するというのはちょっと避けたい.
磁石の作る磁場の形というのは,S と N の二つの単磁荷を用意してやって,双極子とすれば単純化できそうだ.いや,双極子の作る磁場というのは結局は二つの単磁荷の作る磁場の和でしかないのだから,とりあえずどちらか一方の磁荷だけで別々に計算して,後で和を取ってやればいいのではないだろうか・・・?いやいや,わざわざ双極子にしなくても,一つだけでいいじゃないか.要するに,導線の輪をくぐる磁力線の本数が変化すれば起電力が生じて電子が回るのだから,磁石の代わりにモノポールを近付けるという設定に変更しても問題ないはずだ・・・.これなら磁場の形は単純だ.これだけで私の 30 分以上が費やされた.
次に電場の方だが,どう考えようか.リング状に分布する電荷ではなくて平面上に一様に分布する電荷について考えるなら,計算するまでもなくて楽なのになぁ,と思う.その場合は平面を境にして上下にまっすぐ向いた一様な電場になることが良く知られている.これを利用できないだろうか.つまり,ただ一つのコイルを考えるのはやめて,半径の少しずつ違う多数の一巻きの円形コイルを密に配置してやって平面を埋め尽くしてやるわけだ.こうすれば,それらの上の電荷の集団の作る電場は非常に簡単で,計算しやすくなる.これは結局は導体の円板を考えるのと同じことかも知れない.少し問題の設定が変わってしまうが,本質が変わるわけではないだろう.
しかし導体の円板上に静電気を一様に貯めておくことはできるだろうか.電荷は導体上を自由に移動できるので,一瞬にして外周部に集まってしまうだろう.だから設定としては導体円板ではなくて,やはり,互いに絶縁された多数の円形コイルの集まりをイメージしておくのが無難ということか.いや,こうなったら導体にこだわらなくても良さそうだ.電磁誘導によって電荷が力を受けることを考えているだけなので,電荷が一様に分布した絶縁体の円板を想定すればいいわけだ.
しかしまだ問題がある.電場が一様になるのは平面が無限に広い場合だけだ.有限な円板の場合には端の方で形が崩れてしまうのである.どうしたらいいだろう.まぁ,この点にはしばらく目をつぶろう.どうせ厳密に証明したいわけではないし,半径の大きいところにいくほど磁荷から遠いわけだから,ポインティングベクトルも次第に小さくなって無視できるかもしれない.
こうして,設定は少し変えたが計算しやすいモデルが出来た.磁荷を円板の中心軸に沿って近付けて行き,距離
を変更するとき,円板上の電荷の集団は一体どれほどの角運動量の変化を受けるのか.
一方で,ポインティングベクトルはどうなっているだろう.磁場は単磁荷を中心に放射状に伸びており,それと一定方向に向かう電場との外積を計算してやることになる.それは円板の中心軸の周りを回るようなベクトルとなる.それをで割ったものを運動量密度だと見なすなら,それに軸からの半径
を掛けた上で円周に沿って積分したものは,静電磁場の持つ角運動量を表すことになるだろう.

あれれ?コイルの下側では,静電磁場の角運動量の方向が,電子の流れの作る角運動量の方向と同じになってるなぁ.これじゃあ,角運動量保存にならないではないか.ああ・・・でもコイルの上側では逆向きになってるから,そっちの方が大きければいいわけか.ちょっと初めに考えていたイメージと違うなぁ.
果たして,電磁誘導による角運動量の変化量と,ポインティングベクトルによる角運動量の変化量はうまく関連付けられるだろうか.
電磁誘導による計算
まず,電磁誘導によって円板がどれだけ回転するかを計算してみよう.磁荷の接近により,半径
の円形コイルを貫く磁束がどれだけ変化するかを考える.磁荷の定義はそこから出る全磁束と同じだとしよう.つまり
本の磁力線が出ているというわけだ.その内の何本が距離
だけ離れた半径
の輪の中をくぐっていることになるのだろう.

それは上の図で,半径の球の表面の一部を通過して出てゆく磁力線の数と同じだと考えられる.だからその部分の表面積と,球の全表面積との比が分かればいいのである.それは角度
さえ分かれば求められる.立体角の考え方を使おう.半径 1 の球面の面積は
である.一方,半頂角
の円錐が半径 1 の球殻から切り取る部分の面積は
となる.この公式の説明は省かせてもらうことにする.(私も面倒くさいからそこら辺から結果だけ拾ってきたのだ.)これに,
を当てはめれば,コイルを貫く磁力線は,
と計算できる.電磁誘導の法則によれば,これを時間で微分すればコイルの起電力が求められるのだが,この式にはまだ時間が入っていない.それで磁荷を近付ける速度を
として
と置くことにしよう.これでごちゃごちゃと計算すれば,起電力は
である.これを円周の長さ
で割ると,電場の大きさが出る.これに電荷の大きさ
を掛ければ電荷に働く力を表すことになるし,さらに回転半径
を掛ければ力のモーメント
を表すことになる.
しかしこれでは半径
のところにある電荷
に働く力のモーメントになっている.今の設定では電荷は面密度
で一様に分布しているというのだから,それを取り入れたい.
の代わりに,微小面積
内にある電荷,すなわち
を使うべきだろう.
これを半径 0 から
まで積分すれば,半径
の円板全体にかかる力のモーメントが求まるというわけだ.
これを時間で積分すれば角運動量が求まるのだろうが,どちらかというと角運動量の時間変化に興味があるので,この形のままにしておいた方が都合が良さそうだ.
ポインティングベクトルによる計算
次はポインティングベクトルの計算だが,空間の全域を積分するのは無駄だ.微小時間で磁荷を
だけずらしたときの差がどうなるかを知りたいだけなのだ.電場の向きがどこも一定なので,位置をずらしたところでほとんどの場所で変化はない.変化があるのはコイルのある平面のすぐ傍の領域だけだ.この厚み
の平面領域だけは,磁場に掛けるべき電場の向きがひっくり返るのである.
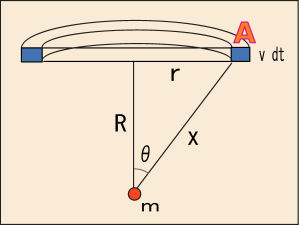
磁荷から距離
だけ離れた点では磁束密度の大きさは
と表される.なぜなら先ほど,磁荷
というのは全磁束と同じだという定義を採用した.その密度,つまり磁束密度は,半径
の球の表面積で割った値になるというわけだ.磁場の強さ
はこれを
で割った値であり,ちゃんと電荷と電場の関係に似た形になっている.
それで,図の A 地点でのポインティングベクトルの大きさは次のように計算される.
これを
で割ってやれば運動量密度になり,さらに半径
を掛ければ,角運動量密度(?)になる.微小面積
,厚み
の領域内ではどこもこの値であると考えて,その微小体積を掛けてやれば,微小領域に限った角運動量が求まるというわけだ.
さて,磁荷が
だけ移動した後にはこの領域の電場の符号が反転するわけだから,角運動量の変化量はこの値を 2 倍したものである.さらに,それを
について 0 から
まで積分すると,円板領域の変化分が計算できる.
これは,円板の領域に限ってはいるが,微小時間
内での角運動量変化を表しているわけだ.
ここで,
と置いたことを思い出せば,前に求めたものと全く同じ値になっていることが確かめられたわけである.
残念ながら,円板の端での電場が計算に使ったような理想的な形でなくなることを無視してもいいとは言えないようだ.半径が増えるほどに
の増加分が減ってくれるという形にはなっていないからだ.しかしながら,端の方が中心付近よりも極端に重要という感じでもない.
あまり厳密ではないが,イメージからかけ離れた感じにはなっていないことが確認できたので,まぁ満足である.
アラゴーの円板
今回の実験は,装置の配置の上では「アラゴーの円板」という有名で手軽な実験に良く似ている.吊るしたアルミ板に磁石を近付けると,磁石に付かないはずのアルミ板が磁石に吸い寄せられるように動くので,磁石をうまく動かしてやれば円板を回転させることもできる,というものだ.家庭内でも簡単に再現できる.洗濯機やら,あちこちで使われている,誘導モーターの原理である.
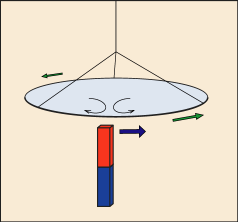
見た目は似た感じの設定ではあるのだが,同じようには行かないものなんだなぁ. まぁ,そりゃそうか.あれは金属内の多量の自由電子が相手なのだからな.
えーっと,磁石と自由電子との相対運動によってアルミの内部に渦電流が発生して,その影響で回転が始まるんだったっけ.あれれ,なんでこっちの実験ではアルミ板がそう簡単に回転するんだ?だって,自由電子以外の部分はプラスの電荷を持ってることになるから,電子の流れとは反対向きの力を得て,全体としては動かないのではないだろうか.
ああ,忘れてた.その渦電流と磁石の相互作用でこのような現象が起きるのだった.だから磁石の方も電流から反作用を受けている.作用-反作用が分かりやすい例であり,今回の話とは全く別物だ.










