ストークスの定理とは
ストークスの定理はベクトルが定義されている空間内での線積分を面積分に変換する便利な公式である.考え方はガウスの定理に似ているが,完全に納得するためにはガウスの定理より少々の根気が必要かもしれない.しかし一度イメージが出来てしまえばとても理解しやすい公式である.ストークスの定理は次のような式として表される.
この中に出てくる
という部分はガウスの定理の中に出てきた
と同じように略記号であるが,
が単なるスカラー量だったのに対してこちらはベクトル量である.よって次のような
,
,
の 3 成分で表現しなければならない.
これはベクトルの回転を表す量なので「rotation」を略して
と書く.教科書によっては
と表記しているものもある.この面倒な組み合わせがなぜベクトルの回転を表すのかという説明は最後にすることにしよう.
式の意味
上に書いたストークスの定理の左辺は線積分になっている.線積分をするためにはコースを決めなくてはならない.この定理の場合どんなコースを選んでもいいのだが,ただ一つの条件として空間内をぐるっと一周した後で元の位置に戻ってきて輪を作るようなものでなければならない.そしてその輪の上の微小な長さの線分を考えて,その点でのベクトルとの内積を取る.内積を取るということは,微小線分と同じ向きのベクトル成分だけを取り出して微小線分の長さと掛け合わせるということである.もし考えているコース上のベクトルの中に,このコースと同じ向きの成分が多く含まれていれば左辺の値は全体としてプラスになる.つまり左辺がプラスになる場合,このベクトルはこのコースに沿って渦を巻いていると言えなくもない.丸い渦ではないかも知れないし,部分的に逆流しているかも知れないが,全体として輪を描く成分が多く含まれているということである.
次に右辺についてだが,こちらは面積分になっている.この時に積分する面としてどのような範囲を考えれば良いかと言えば,先ほどの左辺の線積分で選んだコースで囲まれた面である.このために先ほどの線積分のコースはぐるっと輪になっていなくてはならなかったのである.そうでなければ有限の範囲の面が定まらない.面の形については線で囲まれていればどんな形の面を考えてもよい.膨らんでいてもでこぼこしていても構わないということだ.この面の上に網戸のような細かい網が張られていると考えてみよう.その小さな四角形一つの面積をとする.また,
はこの微小な面に垂直な単位ベクトルである.その多数の各四角形上で計算できる量
はベクトルであるが,これと
との内積をとることで面に垂直な成分のみを取り出すことが出来る.この操作によりベクトルではなくなるわけだ.この値と微小面積
とをかけあわせて全部を合計した量が左辺と等しくなるというわけである.
右辺の計算に一体どんな意味があって左辺と同じになるというのだろうか?
ガウスの定理を説明したときと同じパターンでいってみよう.とりあえず一つのことを認めてもらえばこれをイメージするのはそれほど難しいことではない.それは,右辺の中のの部分が微小な四角形の周りの渦を意味するということである.ここでいう渦とは上で左辺の説明をしたときと全く同じ意味での渦である.微小な四角形の周りに沿って一周の線積分した値が
になるということである.なぜそうなるのかは最後に説明するのでとりあえずそうなのだと信じてもらうことにしよう.
微小な四角形のうちのある一つに注目し,さらにその一辺に注目しよう.どの四角形の周りでも右回りに線積分をしているとすると,この一辺に沿った線積分は,その隣の四角形ではその辺を逆向きにたどって計算を行っているはずである.つまり,一つの微小な四角形の一辺で計算された量は,同じ辺を共有するすぐ隣の四角形の計算で打ち消されてしまうのである.
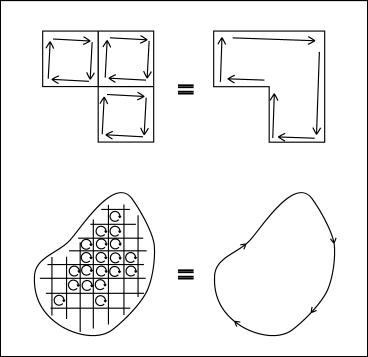
それで全体を積分した時にはほとんど全ての辺についての計算が打ち消されてしまうことになる.例外的に打ち消されずに残るのは面の縁に沿った辺だけだということになり,それは左辺で計算したのと全く同じ部分である.
こう考えれば,両辺が等式で結ばれることは当然納得がいく.残る問題は,本当にが微小四角形の周りの線積分を表しているのかというところだ.
なぜ rotE が回転を意味するのか
ここからが一番説明の面倒なところだ.がベクトル量なので 3 つの方向について説明しなくてはならない.とりあえず,微小な四角形の面が
方向を向いていた場合を考えよう.すると微小な面積
は,
で表すことが出来る.また 面に垂直な単位ベクトルも
方向を向いているので
との内積をとると
の
成分だけが残る.よって,
は次のように簡単に表現できる.
これで二つの項が出来上がったわけだが,これらが微小四角形の周りの線積分を表していることが分かるようにここから変形するのは多少強引だと思うので,逆に線積分を計算してみてこれと同じになることを示すことにしよう.
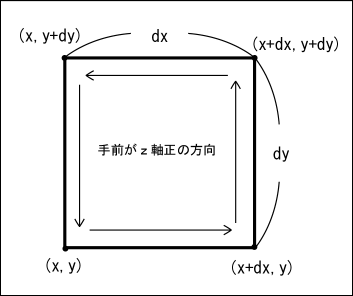
微小四角形の周りの線積分をするために次のコースを選ぶ.まずを出発.
方向へ
だけ進み,
へ.そこから
方向へ
だけ進み,
へ.さらにそこから
方向へ
だけ引き返す.別の言い方をすれば
だけ進む.これで
へたどり着いた.そしてスタート地点へ戻ってくるために
だけ進む.
一見,左回りをしているようだが,これは軸に対して右回りになっていることに気をつけよう.右ねじの法則と同じで,右ねじがこのような回転をした時に進む方向が
軸の方向になっている.
この時の線積分を計算すれば
となる.これについて少し解説を加えておこう.まず,
は計算にあまり関係ないという理由で省いてあるだけなので気にしないように.いちいち書いていたらごちゃごちゃして見にくくなるだろう.さらに,ここで微小長さだけ移動する間にはベクトルの値は変化しないと見なして計算を行った.だからいちいち積分しなくてもこのように簡単に表現できるわけだ.微小領域を考える時にはこのような考え方が使えて便利である.また
方向に進むときにはベクトル
の
成分の値をかけて,
方向に進むときには
成分の値をかけている.これによってストークスの定理の左辺を計算した時に微小線分との内積をとったのと同じことを実現している.
よく見るとこの中にごまかしがあるのに気付くだろう.なぜでの値だけを使って,
での値を使わないのだろう?本当にベクトルの値が変化しないと見なしてよいのだろうか?そういうことに対して問題意識を持つことは,分からないまま受け入れるよりも大切なことである.
話を進める前にこの疑問に答えておくことにしよう.まず,を使わないのは今後の計算の都合である.そのために,
でのベクトルの値と
での値は本当は違うかもしれないが,今は位置的に微小な違いしかないのでほとんど同じだと考えることにしている.そして便利なことに数学上,こういう事をしても構わない仕組みになっているのである. それはこういう理屈だ.仮に,そんな大雑把な考えは許せないのでその変化分も計算に入れたとしよう.しかし位置的に微小な違いなので一定の割合
で変化していると見なせるというくらいのことは微積分の基本的な考えであるので認めてもらいたい.そうすると,例えば初めの辺の線積分は正確には次のようになる.
なぜこうなるかという説明は必要だろうか?私の学生時代のことを考えると念のため説明しておいた方がよいだろうな.初めのベクトルの
成分の値は
で,
だけ進む間に
だけ増加する.つまり,
進む間に
になるわけだ.一定の割合で増加しているので,これらの平均を取って計算してやったというわけだ.これを見ると,後ろの項には
が 2 回かかっている.微積分の考え方ではこの
を無限小にまでした極限を考えるのであるから,後ろの項は前の項に比べて数学的に十分無視しても良いものである.他の辺についても同様な考えが使われているわけだ.
これで計算上の疑問が解決したので先に進むことにしよう.先の線積分の結果を変形してやれば
となる.
,
についてまとめてやっただけだ.第 1 項目のカッコの中身は
方向に
だけ位置変化したときの
の変化量を表しているので,変化率
を使って
と書ける.第 2 項目のカッコ内も同様に
と書ける.つまり,これで前に出てきた式と同じ形になることが分かる.
これでようやく微小な四角形が軸方向を向いていた場合についてだけ,
が微小四角形の周りの線積分を表していることが説明できた.面が他の方向を向いていた場合についても同じようなことが言えるだけなのでいちいち説明する必要はもうないだろう.
の
成分と微小面積
をかけたものが,面が
軸方向を向いていた時の渦を表しているということは,
の
成分である
の部分が表しているのは
平面内の単位面積辺りのベクトルの渦の量だということになる.この量が
の
成分に収まっており,
成分も
成分も同様なことになっているということは,
がベクトルの渦の軸方向を示すベクトルになっているということである.つまり,
が指し示す方向に対して右回りの微小な渦がその点に存在しているということである.










