目的
今回はアルファ崩壊の起こる仕組みをざっくりと紹介する.実のところ,これから話していく素粒子論の話の中にアルファ崩壊が登場する機会はほとんどない.一方で,ベータ崩壊というのはかなり基本的な現象であって,ずっと後の方まで付き合っていくことになる.それでいつまで経ってもベータ崩壊の話しか出てこないのはなぜだろうという疑問を持たなくて済むように,ここでケリをつけておくのである.なるほど確かに今後の話とは関係なさそうだと納得してもらうのが今回の目的である.
それだから,あまり詳しくて正確な話をするつもりはない.というより,今回限りの短い話でそれは不可能というものだ.原子核というのは多数の粒子が集まって出来ている塊であり,その中で起きていることはかなり複雑である.それを理解する為に原子核物理という広大な分野が拓けているほどである.
とは言え,投げやりな説明をするつもりはない.確率的に起こる現象の中身がどうなっているのかを大まかにでも知っておくのは重要だろうと思う.
原子核の内部の様子
原子核の中の陽子や中性子も量子力学に従って運動している.量子力学を使って原子の構造について考えた時のことをちょっと思い出してみて欲しい.今にして思えば,あれは簡単だった.何しろ中心に巨大な質量を持つ原子核があって,その周りを小さな電子が回っていることを考えればいいのだった.しかし原子核は違う.どれも同じような質量を持った粒子が集まっているのだから,どれが重心だということもなく運動している.
このように原子の構造とはだいぶん違っているのだが,似ている部分もある.それは粒子のエネルギーが離散的であり,限られた軌道しか取れないというところだ.だから粒子は低いエネルギー準位の方から順に埋まっていくし,許された軌道をちょうどいいところまで埋めてしまうと安定するという性質もある.原子の場合はこれらは K 殻,L 殻,M 殻などと呼ばれ,これらの殻をぴったり埋めている原子は周期律表の上で縦に並ぶという似通った性質を持つのだった.
原子核もこのような殻構造を持つと考えるとうまく説明できる現象があり,原子核の安定性の一部分はこれによって理解できる.原子核の質量数が小さな場合にはこのような「殻モデル」が有効であるが,質量数が大きくなってくると複雑さが増してしまって,これに基づいた計算は次第に困難になってくる.
質量数が大きな核種の場合には別の要素も入ってくる.多数の粒が集まってブヨブヨに太った原子核というのは,まるで水のしずくのような振る舞いをするのである.原子核の全体が回転したり,ぼよん,ぼよんと全体が変形するような振動をしたりする.そのような回転や振動のエネルギーもまた量子力学に従って離散的な準位を作るのである.このような考えを「液滴モデル」と呼ぶ.
人間にとっては現象をあるがままの形で調べるのは難しいので,このように単純化されたモデルを仮定して考えるのである.もしそれで色々な現象がうまく説明できれば,そのモデルはかなり現実に近い状況を表しているのだろうと言えることになる.
核力と中間子
原子核という小さな領域に押し込められた陽子の間には,正電荷どうしの反発力が相当な強さで働いているはずだが,核力というのはその強さをはるかに凌いでいて原子核をまとめている.
もしそんな強い力が電気力のように遠距離にまで届くなら,世界中のあらゆる原子核は互いに引き合って一つになってしまうだろう.しかし実際にはそうはなっていないのだから不思議だ.
となると,核力というのは電気力のような「距離の 2 乗に反比例する」タイプの力ではなくて,距離が離れるに従って電気力よりも遥かに急激に弱くなる性質を持った力であるに違いない.このことを言い表すために「近距離力」という言葉が使われる.近距離だけで働く力だという意味だ.理論上は遠方にまで届いてはいるのだが,少し離れただけで,電気力と比べて完全に無視できるくらいの力になる.
湯川秀樹はそのような力の原因を説明するために,新たな理論を提案した.1935 年のことだ.電磁気の力が光の粒子の交換によって説明できるという「場の理論」は量子力学の建設が一段落ついた 1925 年の頃からすでに議論され始めていた.光は質量のない粒子である.ではその代わりに,質量のある粒子の交換によって働く力があるとしたらどうだろう.それがまさに,核力のようなタイプの力になるのである.
数式を使った説明は第 2 部以降でやることにしよう.
その粒子の質量がどれくらいだったなら核力と同じになるかを計算してみると,それは陽子や中性子のような重い粒子と,電子のような軽い粒子の中間くらいであったことから,「中間子」と名付けられた.湯川はそのような未発見の粒子がきっと存在するだろうと予言したのである.
それは 1947 年になってようやく発見された.その間,理論でも実験でも色々な発展があって,そう単純に「湯川が正しかった,おめでとう」と終わらせていい話でもないのだが,ここではこれくらいにしておこう.それにしても・・・ここまで来ると,もう戦後のことなんだねぇ.ついこの間のことのようじゃないか.
斥力もある
実験により,原子核の半径というのはおよそ次のように表せることが分かっている.
ここで
と書いたのは質量数である.これを見て原子核の小ささに驚いているだけでは十分ではない.もっと別のことに気付いて欲しいのだ.ここからどんなことが読み取れるだろうか.まず,球の半径と体積の関係に似ていると言えるだろう.質量数
がそのまま体積と同じような意味を持っているではないか.
つまり,どれだけ粒子が増えようとも,一つ一つの粒子の占める体積はギュッとちぢこまったり広がったりはせずに,原子核全体としても常に同じような密度のままだということだ.核力はとてつもなく強力だというイメージがあるかも知れないが,その引力によってどこまでも小さく潰れてしまうということはなくて,ある距離以下には縮めないような強い斥力も働いていると考えられる.あたかも,しっかりとした硬さのある多数のボールが引っ付き合っているようなイメージがぴったりなわけだ.
核力の到達距離から考えてみても,どうやら核力はすぐ隣の粒子とだけ強く結びついていて,隣の隣の粒子ともなるとあまり強くは結びついていないようだ.何だか思ったよりもゆるいイメージだなぁ.個人的な感想を言えば,表面に糊の付いたボールというか,ご飯粒のかたまりみたい.まぁ,その糊がめちゃくちゃ強くて,そのくせ,ネバネバしているわけではないので,互いの周りを自由に回れるというイメージの違いはあるのだけれど.
陽子と中性子は仲がいい
もう幾つかの原子核についての豆知識を披露しておこう.陽子も中性子も電子と同じくフェルミオンである.つまり同じ状態には一つずつしか入ることができない.例えばひとつの陽子が低いエネルギーに入ってしまうと,他の陽子は同じ低いエネルギーに入ることができない.しかし中性子は,陽子とは別の状態の粒子であるから,低いエネルギーに入ることができる.こんな具合であるから,原子核は陽子ばかりであったり中性子ばかりであるよりも,陽子と中性子が同じくらいずつあった方が全体にエネルギーが低く抑えられ,安定でいられるのだ.
同じような理由で,陽子のすぐ周りには中性子が,中性子の周りには陽子が位置しようとする傾向がある.(量子力学的な状態というのは位置と運動量を組にしたものであるから,同種粒子が同じような位置を占めることもなるべく避けようとするのである.)特にというのは殻構造の観点から見てもかなり安定な状態である.それだから質量数の大きな原子核の内部では,このような小さなグループが幾つもできていて,それぞれがひとかたまりで運動しているような傾向もあると考えられる.
それでも質量数が大きくなるにつれて中性子の割合が多い方が安定するのは,やはり中性子と陽子の電荷の違いによるものだろう.粒子の間に反発力があると近くに寄せ付けておくために余分にエネルギーが要ることになるから陽子よりも中性子の方が経済的なわけだ.だからと言って全てが中性子になってしまうのも先ほど話した理由でエネルギーが多く要る.そういう兼ね合いで決まるわけだ.言うは易しいが,それを実験に合うように理論的に計算して示すのは色々と難しいのである.
ヘリウム核が飛び出す仕組み
以上のような生半可な知識があれば,アルファ線が一定の確率で飛び出してくる理由が説明できるだろう.
同種電荷の間には互いに相手を寄せ付けないようなクーロン斥力が働いている.そのポテンシャルエネルギーを図で表すと次のようである.
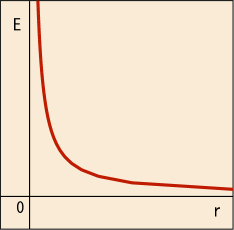
横軸が粒子どうしの距離を表している.互いに近づくためにはこのポテンシャルの無限の坂を登る必要があるのだ.これを「クーロン・ポテンシャル」と呼ぶ.式の形はである.
一方,核力は引力であり,電荷の反発力より遥かに強いので次の図のような深くて急なポテンシャルとして表される.
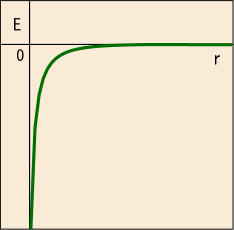
これは湯川秀樹にちなんで「湯川ポテンシャル」と呼ばれている.式の形はである.ある程度より近付くと強い反発力があることから,実際には次のような形になっていると考えられる.
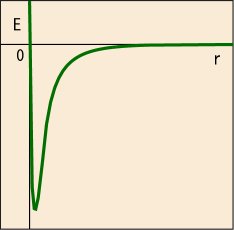
その他に遠心力などのポテンシャルも考慮すべきだが,話の大筋にあまり影響はない.核力と電磁気力の二種類の力のポテンシャルを合成すると,おおよそ次のような形になっていると考えられる.
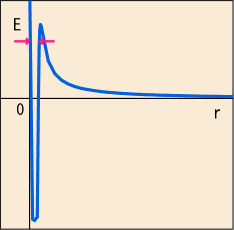
量子力学の例題に出てくる井戸型ポテンシャルに似たような状況である.このような狭い深みの中で,原子核中の電荷を持った粒子は脱出することもできず,激しく運動しているのである.
ところが質量数が大きくなってくると,粒子はエネルギーの低いところにばかり集中していられないので,かなりエネルギーの高い軌道を回る粒子も多くなってくる.なおかつ,原子核の直径が大きくなってくると,遠くに位置する粒子からの束縛を受けにくくなるということもあるだろう.そのような粒子はこの井戸のかなり上の方のギリギリに位置していることになる.
そしてその辺りの薄くなった壁に向かって何度も体当たりするのである.古典力学ではこのポテンシャルの壁はそう簡単に越えることはできないはずだ.しかし量子力学にはトンネル効果というものがある.何度も体当たりするうちに,たいへん低い確率ではあるが,壁の向こう側へ抜けることが出来るのである.
無事ポテンシャルの壁を通り抜けることのできた粒子はクーロンポテンシャルの坂を駆け下り,勢い良く原子核から離れて行く.これがアルファ線の正体である.以上の説明で,アルファ崩壊が質量数の大きな核種でのみ起こることの理由も理解できるであろう.このようにして原子核の中から 2 個の陽子と 2 個の中性子が出て行くのだから,原子番号が 2 つ下がり,質量数が 4 つ下がる.
どうだろう.物質の根本とはあまり関係のなさそうな,かなり応用的な匂いのする現象であることが感じてもらえただろうか.
しかしながら,こういう現象を細かく調べることによって,根本的な現象の性質を深く知ることの助けになるのだということは忘れてはいけない.実際,核力の性質にはまだまだ理解の難しいことが色々と残されているのである.










