素粒子論：素粒子の分類作業

奇妙な粒子のストレンジネス

加速器によって数百もの新粒子が次々と発見された.また,それらがどのような反応によって生み出されるかという膨大な知識も蓄積されていった.

それらを分析することで,そのほとんどが同じ粒子の励起した状態を見ているのだということが分かってきた.つまり,余分なエネルギーを放った後の比較的安定な粒子だけを使って考えるようにすることで,状況がかなり整理されて見えてきたのである.

それでも,どの粒子とどの粒子が同一であるかという判断は慎重に行われたし,本当に同一の粒子であるのかどうか,最後まで研究者たちを悩ませるような粒子もあった.その話は別の機会にしよう.粒子の対称性に関係するのでここで説明すると少しややこしいことになりそうなのである.

反応の前後で電荷やスピンが保存するのと同じように,他にも保存する量があると仮定すると粒子の分類がうまく行きそうだった.その保存量は色んな研究者によって色々な呼ばれ方をしていたが,やがてそれは「ストレンジネス」という呼び名で定着するようになった.

「ストレンジネス」とは「奇妙さ」という意味でもある.ストレンジ粒子（奇妙な粒子）と呼ばれた何種類かの粒子があり,それらが +1 とか -1 とか -2 とかの整数値の「ストレンジネス」を持っていると考えられた.奇妙ではない粒子のストレンジネスは 0 である.

それらストレンジ粒子のどこが奇妙だったというのか.高エネルギーの「奇妙でない粒子」（ストレンジネスが 0 の粒子）どうしがぶつかった結果としてストレンジ粒子が生み出される時には,必ずストレンジネスを保存するかのようにプラスのストレンジネスを持った粒子とマイナスのストレンジネスを持った粒子が一緒になって出てくる.しかしこれらはやがて,ストレンジネスを持たない粒子へと崩壊してしまうのである.

生まれる時にはストレンジネスが保存するかのように振舞い,崩壊する時にはストレンジネスは保存しないようなのだ.

これについてはもう少し正確に説明しておかないといけない.このストレンジ粒子というのは前回の話で出てきた V 粒子のことである.前回の話では「V 粒子は滅多に見付からないが,見つかるときは直後に崩壊してしまう」と説明したのだった.しかし加速器が進歩してくると,これらの粒子は頻繁に見付かるようになった.そしてエネルギーの高いストレンジ粒子は他の粒子と衝突したりして様々な反応を引き起こすわけだが,それでもストレンジネスは必ず保存しているのだった.ストレンジネスを保存しないような奇妙な崩壊を起こすのは,それと比べたら「めったに起きない現象」だと言えるくらいになってきた.

このストレンジ粒子が「奇妙な崩壊」を起こすまでの「長い寿命」はベータ崩壊と同じ理論で説明できる.V 粒子の説明をしたときには「すぐに崩壊する」と書いたが,素粒子の寿命としてはかなり長いのである.なぜ寿命が長いかと言えば,ベータ崩壊と同じ「弱い相互作用」でしか崩壊できないからである.弱い相互作用は,起きる確率が低く,核力などの原因である「強い相互作用」と比べると滅多に起こらない現象である.一方,強い相互作用の方はストレンジネスを失わせることができないのだ.

このようにまとめることができる.「ストレンジネスは強い相互作用では保存するが,弱い相互作用では保存しない.」

スピンによる分類

ストレンジネスによる分類の他に,スピンによる分類もできる.スピンは角運動量と同じようなものであり,反応の前後でちゃんと保存するのである.そのような事実を利用して未知の粒子のスピンを特定することも可能だった.

スピンが整数値を取るものを「中間子族」と呼ばれるものに分類し,スピンが 1/2 の奇数倍であるものを「バリオン族」へと分類した.バリオンとは,「重い粒子」という意味である.ギリシャ語の barys（重い）に由来しており,英語では baryon と書く.「重粒子」と訳されることもある.

ちなみに,中間子の方は英語では meson であり,これはギリシャ語で真ん中を意味する mesos に由来している.日本語で「メソン」とか「メゾン」とか表記されることもある.

スピンと統計の法則から分かるように,中間子族はボソン（ボーズ統計に従う粒子）であり,バリオン族はフェルミオン（フェルミ統計に従う粒子）である.

アイソスピンによる分類

この他に,アイソスピンによる分類もできる.アイソスピンというのは元々陽子と中性子が同じ粒子でありながら状態が違うだけのものだという仮説によって導入された概念であった.多数の陽子と中性子が集まったものである原子核の振る舞いを説明するために,粒子のスピンを表すのと同じ数学を借りてきて議論したのだった.

粒子のスピンの合成は単なるベクトルの重ね合わせではなくて多少面倒な考え方を必要とするのだった.多数の陽子と中性子の集まりである原子核を議論する時にもこれと同じような重ね合わせの考え方が使えるのだった.

さて,今やアイソスピンの概念は陽子と中性子だけではなく,湯川の予言した中間子の理論にも使われていた.陽子と中性子のアイソスピンの大きさは |I|=1/2 で,その成分には I_z =1/2 と I_z =-1/2 の 2 通りがあり,それぞれを陽子と中性子に割り当てた（核物理では逆に割り当てられている）のだった.一方,中間子理論によれば,中間子のアイソスピンの大きさは |I|=1 であり, I_z =1 , 0 , -1 の 3 種類の中間子があることになる.それらは予言の通りに見付かったのだった.

このアイソスピンの合成の概念が素粒子の反応でも使えて,アイソスピンは反応の前後で保存すると考えても良さそうだった.しかしそれはいつでも必ず保存するというわけではなく,対消滅的な反応の時には消えてなくなってしまうものではある.弱い相互作用の時にも保存していない.それでもほとんどの場合には使えそうだった.

法則化の第一歩

このように試行錯誤で粒子に数値を与えて行って分類してゆくと,面白い規則性が得られることになった.主要な粒子が,次の図のようなパターンの上に乗って来るのである.

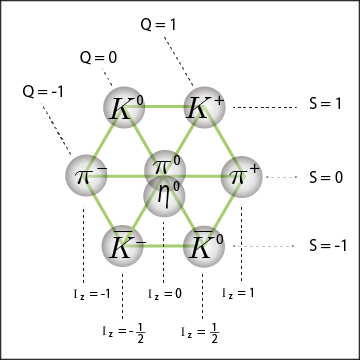
これは中間子族についてだけまとめた図である.縦軸にストレンジネスを取り,横軸にアイソスピンの成分を取って並べると 6 角形になる.そう並べたのだから当たり前と言えば当たり前だ.中央には二つの粒子が入っているので,同じ属性を持つ粒子は一つずつしかないなんてことも言えない.しかし大事なことが見い出せる.どうやら電荷の値が他の二つの量,アイソスピンとストレンジネスと関係しているらしいということだ.

各粒子の右上に書いてある符号が電荷の量を表しており,同じ電荷量を持つ粒子が斜めに並んでいるのが分かるだろう.

バリオン族についても次のように同じような図になる.

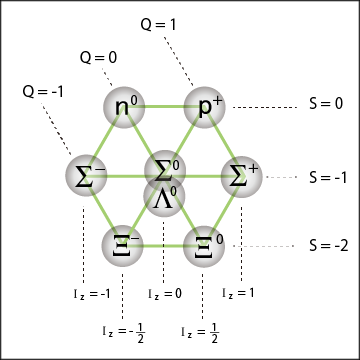
ストレンジネスの位置が先ほどとは少しだけ違うが,やはり電荷とアイソスピンとストレンジネスには規則性があることが分かる.しかも,粒子の入り方が先ほどと似ているというところも怪しい.裏に何か有りそうだ.

さて,中間子族の図には,粒子と反粒子が同じ図の上に描かれていた. $K^{0}$ の反粒子は $\overline{K}^{0}$ と書いて表しているし, $K^{+}$ の反粒子は $\overline{K}^{-}$ である.また,電荷を持ったπ中間子である $π^{+}$ と $π^{-}$ は互いに反粒子の関係にある. $π^{0}$ の反粒子は $π^{0}$ 自身であるし, $η^{0}$ も同じだ.

しかし,バリオン族の図には反粒子が描かれていない.実は,バリオン族は粒子と反粒子のそれぞれで同じようなパターンを作るのである.反バリオンの図も念の為に書いておこう.

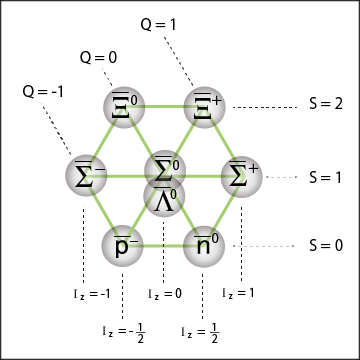
反粒子はストレンジネスとアイソスピンの符号が反転するので,上下と左右を入れ替えた感じの図になっている.

いや実に面白い.無秩序に見えた多数の粒子に,規則性があることがようやく見え始めたのだ！このような分類作業が,新粒子の発見が次々と報告される中で同時に行われていったのである.

この図から読み取れるもの・・・.電荷とアイソスピン I_z とストレンジネスの間には関係がある！中間子族の場合には Q=I_z +S/2 となっており,バリオン族の場合には Q=I_z +S/2+1/2 さらに,反バリオン族の場合には電荷もストレンジネスもアイソスピンも逆転するので, Q=I_z +S/2-1/2 となっている.

場合によって式が違うのは気持ちが悪い.統一することで共通する性質が見えてくるのかも知れない.そこで次のような量を定義してみる. この新たな量を「ハイパーチャージ（超電荷）」と命名しよう.これを使えばバラバラだった法則が次のようにまとめられる. これを「中野・西島・ゲルマンの法則」略して「NNGの法則」と呼ぶ.

実は基本的な粒子は今回の図にあるものだけではなく,まだ特殊なものが色々と見付かるのであるが,それは次回以降を楽しみにしてもらうとしよう.

そう言えば,今回の分類図では電子やミューオンやニュートリノが登場せず置き去りになっているのだが,それもどうなることやら・・・？

参考資料

今回は今まで説明していなかった粒子が突然出てきたので,参考までに,それらの読み方や性質を表にまとめておこう.

当時見つかっていた中間子の代表（反粒子は省略）
大雑把な分類		質量（MeV単位）	平均寿命
（パイ）中間子 pion (パイオン) meson（パイメソン）	$π^{0}$ （パイゼロ）	134.97	0.08フェムト秒
（パイ）中間子 pion (パイオン) meson（パイメソン）	$π^{+}$ （パイプラス）	139.57	26ナノ秒
（ケイ）中間子 Kaon (ケイオン) K meson（ケイメソン）	$K^{+}$ （ケイプラス）	493.68	26ナノ秒
（ケイ）中間子 Kaon (ケイオン) K meson（ケイメソン）	$K^{0}$ （ケイゼロ）	497.67	52ナノ秒 89ピコ秒
（イータ）中間子	$η^{0}$ （イータゼロ）	547.8	0.55アト秒

今のところ粒子と反粒子の違いは観測にかからないほどなので,この表では反粒子を省略してある.

K⁰の平均寿命が二つ書いてあるが,崩壊の仕方が二つあり,少しややこしいことになっている.いつか別の記事で説明するつもりである.

ηはイータと読んでもエータと読んでも構わないので,エータ中間子と読んでも良い.わざわざ中間子と言わなくても,エータ粒子と言えば通じる.そう言えば,パイ中間子をパイ粒子と呼ぶことだってある.上では「イータゼロ」と書いているが,イータ粒子なら電荷はゼロだと分かるので 0 を付けなくても通じる.

当時見つかっていたバリオンの代表（反粒子は省略）
大雑把な分類		質量（MeV単位）	平均寿命
核子	$p^{+}$ （陽子）	938.272	崩壊しないと思われている
核子	$n^{0}$ （中性子）	939.565	887秒
（グザイ）粒子	$Ξ^{-}$ （グザイマイナス）	1321.31	0.16ナノ秒
（グザイ）粒子	$Ξ^{0}$ （グザイゼロ）	1314.86	0.29ナノ秒
（シグマ）粒子	$Σ^{+}$ （シグマプラス）	1189.37	0.08ナノ秒
	$Σ^{0}$ （シグマゼロ）	1192.64	0.07アト秒
	$Σ^{-}$ （シグママイナス）	1197.45	0.15ナノ秒
（ラムダ）粒子	$Λ^{0}$ （ラムダゼロ）	1115.68	0.26 ナノ秒

中性子の電荷が 0 であるのはみんなが知っていることなのでわざわざ n の右上に 0 を書く必要はないのだが,他と形式を合わせるために書いてある.陽子も同じである.

このような表を作って眺めてみると幾つか気付くことがある.ストレンジネスを持つ粒子は少しだけ重そうだな,とか,ストレンジネスが ±2 であるグザイ粒子はさらに少しだけ重そうだとか.しかし他と比べてひどく重いというわけでもないようだ.

平均寿命を見ると,だいたい同じようなものであることも分かる.崩壊を引き起こす仕組みがどれも同じようなものなのだろうということで安心できる値だ.しかし極端に短い寿命のものも少しだけ混じっており,それらは崩壊の原因が他とは違うのだろうかと気になり始める.

それにしても,それらの寿命は短か過ぎやしないだろうか？1 アト秒ともなれば光速で走っていたとしても原子 1 個分くらいを進む間に崩壊してしまうだろう.そんなものをどうやって発見することができたのだろう？そのことでしばらく悩み込んでしまったのだが,光速で走る物体は寿命が伸びたように観測されることをすっかり忘れていたのだった.

これらの寿命の極端に短い粒子は弱い相互作用で崩壊するのではなくて,何か別の要因があるというのだろうか？調べてみると, $Σ^{0}$ 粒子はガンマ線を放って $Λ^{0}$ 粒子へと変わってしまうのだそうだ.これは弱い相互作用ではなく,電磁相互作用の働きである.

しかしそれもおかしいではないか.つまり $Σ^{0}$ 粒子というのは $Λ^{0}$ 粒子の励起状態だということになりはしないだろうか？それなのに $Σ^{0}$ 粒子と $Λ^{0}$ 粒子を同一のものだとせずに,わざわざ別の名前を付けたままにしているのはなぜだろう？おそらく歴史的な経緯というのもあるかも知れない.アイソスピンというのはスピン角運動量と同じ数学を使っているのだった.スピン 1 の粒子というのは |s|=1 に対応して s_z =-1,1,0 の 3 つの状態があり,さらに |s|=0 の状態に対応してもう一つの s_z =0 の状態があり,合計 4 通りの状態があるのだった.それに似たようなものだと考えられているのだろう.

では $π^{0}$ 粒子はどうだろう？これは何と,二つのガンマ線になって跡形もなく消えてしまうのである.これは対消滅に似た現象で,対消滅は電磁相互作用で説明できる現象である.なぜ単独の粒子が対消滅みたいなものを起こすのかというのは,この粒子が実は何で出来ているかが分かれば理解できる.先の話を明かしてしまうと,これは同種のクォークと反クォークが一時的に分子のようなものを作っている状態なのである.

$η^{0}$ 粒子も同様である.二つのガンマ線になって消えることもあるし,中間子よりはるかに重いので,複数の中間子へと姿を変えて飛び散ることもある.具体的には $π^{0}+π^{0}+π^{0}$ や $π^{0}+π^{+}+π^{-}$ が起こる.生成した中間子に運動エネルギーを持たせることで,ガンマ線を放たなくてもエネルギー保存則を保つことができるのである.

$K^{0}$ については複雑な事情があるので多分別の機会に説明することになると思うが,短い方の寿命でもひどく短か過ぎるというわけではない.これらはどちらも弱い相互作用によって起きるものだそうだ.