物理数学：測定値の統計処理

平均を取れば誤差は減る？

偶然誤差というのは測定しようとしている対象の真の値の周囲にバラつくものである.多数の測定を行って平均を計算することで,真の値に近い結果を得ることが出来る.その時,誤差（確からしさ）の程度をどのように見積もって,どのように表現したらいいのかを考えてみよう.

ところで,測定する対象によっては「真の値」と呼べるものがない場合もある.典型的なのは量子現象が絡む場合である.これは自然そのものが,測定のたびに,確率的にバラついた値を返してくるのである.どこまでも正確な測定を行うことができたとしてもやはり値はバラついているというのが,この場合の自然の本性である.

さらに深く考えると厄介な考えに到達する.そもそも我々が実験で得るのは様々な誤差を含んだ測定値でしかない.つまり,我々は決して「真の値」というものを知りようがないのである.こうなるとこの世に「真の値」と呼べるものがあるかどうかも怪しくなってくる.

それでも,「真の値」は存在しているという素朴な信念を持っていた方が理解が楽なので,しばらくはそのイメージで説明を続けることにしよう.

中心極限定理の紹介

ある一つの対象についての測定を繰り返し行ったとき,測定値がある程度ばらついてしまうわけだが,どの値がどれくらい出やすいかという分布をグラフにすると例えば次のような具合になるだろう.

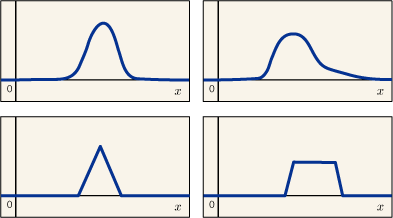
何種類か描いてみたのは,実際にどんな分布になるのかは実験によって違っているからである.横幅を大げさに広く描いているが,実際はもっとずっとずっと狭いことの方が多いはずだ.

測定回数を百回,千回,一万回と増やしていくと,だんだんその分布がはっきり分かってくることだろう.これらの分布のピークあたりが「真の値」だと考えられそうだ.しかし時間やコストや面倒臭さを考えると,ちょっとした実験の測定のためにそこまではできないのである.

そこで,5 回か,せいぜい 10 回くらいの測定を行って,この分布の様子を当てに行くことになる.何回測るかはその時々によって違っているだろうから,この記事では回と表現しておこう.そして回の測定値を使って平均を計算してみる.それはどれくらい「真の値」に近いだろうか？

試しに,この回の測定をワンセットにして何度も何度も測定を行い,無数の平均値を取得してみる.そして,平均値としてはどの値が出やすかったかをグラフにすると次のようになる.

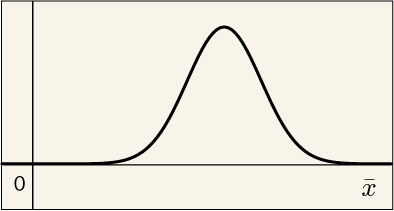
これはガウス分布と呼ばれるグラフである.驚いたことに,元々のバラつき分布のグラフがどんな形をしていようとも,平均値のバラつきに関してはどれもこの形状のグラフになることが数学的に導かれる.これを「中心極限定理」と呼ぶのである.

ちょっと信じがたいかも知れないし,数学的にはもう少し厳密な表現が必要だから,興味が出た人は自分で詳しく調べてみてほしい.かなり少ない前提からこの驚くべき性質が成り立っていることが分かるはずだ.

それはちょっとおかしいと思う人もあるだろう.ガウス分布というのはという式で表されており,ピークからどれだけ離れていても 0 ではない.0 に近付きはするが,厳密には 0 ではない.つまり,真の値から恐ろしくかけ離れた平均値が出てきてしまう可能性も 0 ではないと言っているのだ.ところが現実の測定というのはそうではない.何ミクロンの精度で測定しているときに,何メーターも離れた測定値が出る可能性はないと言っていいだろう.しかしこの違いは気にしなくてもいいほどである.そういう場合に当てはめてみると極めて尖ったガウス分布になるので,両側に少し離れたところではほとんど可能性 0 とみなしていいほどの分布になるのである.

ガウス分布は数学的に扱いやすいので,これを利用して色々なことが推定できる.をどれくらいに上げたなら,どれくらいの確率で「真の値」からどれくらいの範囲に入る値を得ることが出来るのか,という理論が導き出せる.では今からそういう話を始めよう.

期待値と分散

実験値の分布の関数が f(x) という形状だったとしよう.これは無限回の測定を繰り返した末に得られるだろうものだから,観測を行う当人は知らないものである.これはという測定値が得られる確率を表していることになる.だから確率の全体の合計が 1 になるように調整しておこう. 最初に話した素朴な考え方によれば,測定値がバラつく時には平均値を計算すれば真の値に近いものが得られるだろうというのだった.しかしこの分布 f(x) が左右対称の形状をしていなければ平均値はグラフのピークとは一致しない.グラフのピークの部分こそが真の値を表しているのではないかというのもまた,素朴な考えの一つだろう.それでも,平均というのは簡単に計算できて便利だから,この測定全体を代表する数値として重んじることにする.

この分布に従って無限の測定値を得て,それらの値を全て使って平均したものを考えよう.それは「期待値」と呼ばれるものと同じである.期待値というのは確率的に出現する値と,その出現確率とを掛け合わせたものを全て足し合わせて計算するものだが,今回のように確率が連続的に表現されているときには次のような積分で表すのである. なぜこれが平均値と同じ内容であるかというのは次のように考えればいい.測定のデータ数が無限ではなく,代わりにかなり大きな数だとしてみよう. N×f(x) dx というものを考えれば,これは x～x+ dx の範囲の測定値が得られた出現数を表している.それにを掛けながら全範囲について合計したら,つまり積分してやればということだが,データ全体の合計値になる.それを最後にで割ってやれば平均値になるわけだ.は結局消えてしまうし,途中の計算にも影響を与えていない.それだから,はこの式からあらかじめ消えているのである.

期待値の他にも,この分布の形状から比較的楽な計算で得られる数値がある.期待値の周りにどれくらいバラついているかを表すもので,次のように計算できる. この値のことを「分散」と呼ぶ.グラフの形状が横に広がった感じになっているほどこの値が大きくなる.この計算の意味を理解するには,今回のような無限個の分布の話ではなくて,有限個のデータの話を先に知っておいた方がいいかも知れない. $x_{1},x_{2},\dots,x_k$ という個の測定値があった場合に,その平均値を $\bar{x}$ とすると,この場合の分散は次のような計算で求められる. $(x_i-\bar{x})^2$ の部分が各測定値 x_i が平均値 $\bar{x}$ からどれくらい離れているかを意味している.それをどんどん足し合わせて行くと,データが増えるほど数値が大きくなってしまうのでデータの数で割って平均を取るのである.なぜ 2 乗しているかというと,各データは平均値より上にも下にもずれているので,2 乗せずに足し合わせると合計は 0 になってしまうからである.2 乗することで全てを正の値にしてしまって,この問題を手っ取り早く解決したというわけだ.絶対値を使ってもいいではないかと思うかも知れないが,絶対値よりも計算が楽なので多用されるのである.

積分で表した分散の計算はこれと同じ内容のことを意味している.期待値と平均値の関係に似た話であるので同じように考えればいいだろう.

分散というのは,どれだけ測定データ全体のバラつきが大きいかを表している.値が小さいほど測定の精密さが高いことを意味するのである.これは重要なデータだ.

さて,なぜ測定者が永久に知ることのない分布 f(x) についての期待値やら分散やらをわざわざ説明したのかというと,たった回の測定だけでこの期待値や分散の値にどれだけ近いデータが得られるものなのかという推定を話題にしたいからである.

証明なしに語る重要な性質

ここで再び驚く話を紹介しよう.先ほど,回の測定値の平均値ばかりを無数に集めてグラフを作ると f(x) の形に関係なくガウス分布になるのだという中心極限定理を紹介したのだった.このガウス分布のピークは,先ほど計算したと同じになる.

今,さらっと重要なことを言ったつもりである.一瞬驚くかも知れないし,じっと考えてから驚く人もあるだろうが,さらに意味を考えてみれば割りと当たり前のことだ.回の平均を無数に合計して平均を取っても,回ごとに分けずに合計して平均を取っても,結局は同じものであるからである.ガウス分布は左右対称であり,平均値はピークと一致するのだからこれも当たり前だ.

では,分散についてはどうだろう？せいぜい回の測定値だけで計算できる何らかの値と,先ほど紹介した分散との間に面白い関係が見いだせるだろうか？残念ながらこちらはそれほど単純ではない.結論を先に言ってしまうと,まず,回の測定から次のような量を計算する必要がある. 先ほど紹介した分散の計算とは少し違っている.ではなく n-1 で割る必要があるのだ.もしがとても大きくなればこのとの違いは気にならなくなるが,が小さい時にはこの違いが重要なのだ.そしてこの回でワンセットの測定を無数に繰り返して無数のを得た後に,その平均を計算してやると,それが何と,に等しくなるというのである.少しややこしいせいで,素直に驚いていいものかどうかよく分からないかも知れない.こののことを「不偏分散」と呼ぶ.

しかしこれが何の役に立つというのだろう.回セットの測定を無数に繰り返してたくさんのを得ないことにはが求まらないのである.無数の測定が出来るのならを直接求めた方がマシである.もともと無数の測定をするのが現実的でないので回ほどの測定で済ませようとしているのに,を一つだけ得たところで,それがどれだけに近いかは運任せなのである.

ところがこの不偏分散を測定回数で割ったものは非常に重要な情報を持っている. 何と,このは「回の測定で計算した平均値 $\bar{x}$ 」の分散を表しているのである.いや,正確に言うとこのも無数の平均をしてやらないと正確な値にはならないのだが,が 5 や 10 程度であればもうかなり正しい値に近い確率が高く,ハズレの可能性は極めて少ないのである.それについてはまた後で話そう.

いきなりこのようなことを立て続けに言われても,その意味も重要性も想像できないのが普通だろう.しかしこれでようやく準備が整ったので,応用の話に一気になだれ込もう.

利用法

先ほど中心極限定理のところで,平均値を無数に求めてグラフにするとガウス分布になるという話をしたのだった.そして,というのは,そのグラフの分散を意味するというのである.それは f(x) の分散のことではないので混乱しないようにしてほしい.平均値がどれほどバラつくかを意味しているのである.

先ほどのについての式を見ると,測定回数を増やすほど,値が小さくなるのが分かる.つまり,を増やすほど,ガウス分布のグラフの横幅が狭く,尖ってくると言えるだろう.何度も念を押すが,平均値についての分布はガウス分布になっており,はその分布の分散を「だいたい正しく」表している.

話を続けるには分散のルートをとったもので考えた方が都合がいい.分散のルートは「標準偏差」と呼ばれている. 先ほどのガウス分布の式 g(x) の中にもという記号が使われているが,このはそれと同じ意味である.ガウス分布の式 g(x) を使って分散を計算してやってその平方根をとるとちょうどになるようになっている.計算力のある人は試してみるといいだろう.

ガウス分布との関係については良く調べられており,例えば次の図のようなことがいつでも成り立っている.

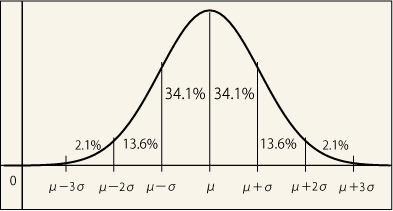
我々が回の測定を行って平均値 $\bar{x}$ を得るとき,その平均値はあたかもガウス分布の中から値を拾っているのだという考え方が出来る.そしてその平均値 $\bar{x}$ はグラフのどこに位置するものかは少しも分からないが,それが中心から以内に入る確率は 68.27 %, ±2σ 以内に入る確率は 95.45 % になる. ±3σ 以内に入る確率は 99.73 % にもなる.

我々が知りたいと思っていた期待値,つまり「真の値」はこのガウス分布の中心に一致するのだった.そこで立場を逆にして考えてやってもいい.我々が探し求めている真の値が $\bar{x}±σ$ の範囲内に入っている確率は 68.27 %, $\bar{x}±2σ$ 以内に入る確率は 95.45 % になるのだと.

さまざまな運用

以上のような理論的背景があるので,回の測定を行ったとき,その平均値を計算して $\bar{x}$ とし,さらに不偏分散を計算してで割ってルートをとったものをとしてのように表記を行うことが多い.業界によってさまざまだが,普通,については二桁のみを残して四捨五入し, $\bar{x}$ はの最終桁までを有効数字として残すのである.

業界によってはを 2 倍した値を表記することもある.工学の一部の分野や,工業の品質管理などではこれを採用する場合も多い.こうすれば約 95 % の確率で真の値がこの範囲内に入っていることになるからである.

これは「拡張不確かさ」と呼ばれるものであり,近年世界的に標準化が進められている「不確かさ解析」の中で規定されている作法である. を何倍にして表示するかを「包含係数」と呼ぶ.

あるいはを使うのではなく,不偏分散をで割らないでそのままルートをとったものを表記する場合もある. これもまた標準偏差と呼ばれ,同様にのように表記されるが,先ほどとは意味合いが違ってくる.これは f(x) というグラフの標準偏差に近い値を表示している.つまり,この測定対象そのもののバラつき具合を意味していることになるのである.これを使うのは「真の値」がどこにあるかということ自体にはあまり興味がない場合に多い.そういうことは物理においても珍しくはない.例えば量子力学的な現象の場合,測定値のバラつきの広がりがどの程度かという情報自体が重要な価値を持つことがあるのである.

これは工業製品の品質管理や,アンケート調査などにもよく使われる.例えば,何百万個もの自社製品の性質のバラつき具合を調べるのに,全てを検査するのは手間がかかるし製品を傷める可能性もあり実際的ではないということがある.そこで,数百個や数千個のサンプルだけを無作為に取り出して調べることで,製品全体の質がどの程度の範囲内にコントロールされているかを推定できるのである.

この場合には製品全体のバラつき具合 f(x) がガウス分布に従っているとは限らないので,全体の何パーセントがどの値の範囲にあるという判断は同じようにはできない.今回の話ではその辺りの説明は省いている.明らかにガウス分布を仮定して使えるのは,平均値の分布を考える場合だけである.

細かいルールの違いは他にもある.不偏分散は n-1 で割ったが,で割って計算した普通の分散の方を使うことに決めている業界もあるだろう.測定回数がとても大きい場合にはどちらを使っても大差はないから,測定のサンプル数が大きいのが当たり前の業界では,よりシンプルな手続きで統一しようというわけだ.

このように業界によって色々なルールがあるので,自分が属する業界ではどのように決まっているかについての確認が大切である.また,誰もが同じやり方を当たり前だと考えて使っているとは限らないので,自分がどのやり方で計算した値を使っているのかというのが分かるような説明を添えることも大切である.

統計は万能ではない

偶然誤差は平均を取ることで減らせるという話をしたのだが,平均を取りさえすればどこまでも正確になるとは限らない.例えば定規で長さを測る場合,1 mm 間隔で目盛りが付いているから 0.1 mm くらいまで目分量で読み取ることになるだろう.しかしこれを 100 回,1000 回,いや 10000 回確認して平均を取ったからと言ってどんどん正確になって何ミクロンまで正しく読み取れるなどというのはあり得ない話だろう.

この理由は,偶然誤差の他に系統誤差があるからというわけでもない.たとえ系統誤差がなかったとしても,この方法で精度は上がらない.

我々は測定値のゆらぎの原因が何であるかをはっきりさせ,統計的手法で精度を上げられる性質のものであるかを検討しなければならない.今の例の場合,読み取りの限界の方が大きくて,ゆらぎの影響を消しても大して意味はないと考えられるわけだ.

先ほど言いそびれたのでここで書いておくが,平均値の標準偏差を 2 倍にするには測定回数を 4 倍に増やす必要がある.元々 10 回やっていたなら 40 回に増やさないと精度は倍にならない.なかなか大変なことである.

また, f(x) の標準偏差の推定値の方は測定回数を増やすほどに正確になっていくが,ある程度以上行えばもう値に大きな変化はない.いや,測定回数によって大きく変わってもらっては困るというものだ.

バラバラな用語

統計学というのは教科書によって用語や記号の使い方がバラバラである.一つの概念に幾つもの別名があったり,それぞれ異なるはずの概念に同じ名前がついていたりもする.色んな分野への応用がされているので,どういう人向けに書かれたかによって,受け入れられやすい表現の仕方がそれぞれ異なるという事情もあるのだろう.

また最近は「不確かさ解析」「不確かさ評価」と呼ばれる世界規格が広がりつつあるので,そちらで使われている用語も混じり始めている.

この記事の準備をしながら,初めのうちは「私がその辺りのバラバラな用語を統一してやろう」などという野望を持っていたりもしたのだが,結局のところ,主流とは成り得ない個性的な説明を試みたせいで,おかしな亜流をもう一つ作ってしまったのだった.言い訳をさせてもらえば,説明の邪魔になりかねない余計な用語や記号をなるべく増やさない方向で努力したのだ.

ここでは,罪滅ぼしのつもりで,他の資料ではどの概念がどのように呼ばれているのかをまとめておくことにしよう.いや,そんなかっこいいものでもないな.むしろ愚痴に似ている.あちこちの本を参考程度にちらりと覗いてみたかっただけなのに,そのたびに用語が違うものだからひどく悩まされたのだ.

この記事中での記号	この記事中で使った呼び方	他の呼び方
	実験値の分布	母分布
	ガウス分布	正規分布
	期待値	母平均,平均値,
	分散	母分散,
（未使用）	（未使用）	標準偏差,母集団標準偏差,,SD
$\bar{x}$	平均値	標本平均,サンプル平均,
	不偏分散	標本不偏分散
	平均値の分布の分散に近い値
	ガウス分布の標準偏差	平均値の平均2乗誤差,
	測定対象そのもののバラつき具合	測定値の平均2乗誤差,,推定標準偏差, $\hat{σ}$

この一覧についてあまりじっくり眺めたり,深刻に考えたりしないでほしい.統一感がないのは色んな文献から拾ってきたからである.今から,このような違いが生じている背景についてざっと説明することにする.

私は物理学における測定を念頭に置いてこの記事を書いたので,測定したときの値のバラつき具合を f(x) という確率分布として幾分か抽象的に表したのだった.ところが統計学の主流の応用先というのは,大量生産される自社製品の品質管理であったり,医療における全国の患者のデータであったり,大規模なアンケート調査の分析であったりする.膨大な数ではあるけれども,全て実在する有限の数の集団を相手にしているのである.それを「母集団」と呼ぶ.イメージとしては関数 f(x) を使うよりもすこしガタガタな棒グラフだったりするし,期待値とは呼ばずに平均値と呼んだ方がイメージに合うだろうし,積分を使って表さない方が受け入れられやすい.だから,そういったものを扱う読者を対象にする場合には,母集団についての平均,分散,標準偏差をそれぞれ「母平均」「母分散」「母集団標準偏差」などと表現するのが自然なわけだ.

物理の測定では回の実験を行うことで,確率分布 f(x) に従う結果を引き当てるイメージだが,一般的には膨大な母集団の中から個のサンプル（標本）を無作為に引き抜いて調査をする.だから,「標本平均」「標本分散」「標本標準偏差」などという用語が出てくるわけだ.

母集団だろうと標本だろうと,分散の平方根を標準偏差と呼ぶことは共通している.こう考えると教科書によって用語はバラバラでもだいたい規則性があって,それぞれの範囲内では筋が通っている.

ところが不偏分散が曲者だ.で割って計算すれば分散であり, n-1 で割って計算すれば不偏分散である.標本数が大きければ,これらにはほとんど違いはないのである.それで,分野によっては読者に違いを意識させる必要がほとんどなかったりする.「標本分散」と言ったとき,どちらを意味するかは教科書によって違っている.

さらには不偏分散の平方根を標準偏差と呼ぶべきか,分散の平方根を標準偏差と呼ぶべきか.どちらにしても,これらは母集団の標準偏差の推定値を意味することになる.

統計学の利用者のほとんどが興味のあるのはこの辺りまでである.彼らにとって「真の値」を特定することに意味はないのだ.製品にも患者にもアンケートにも真の値と呼べる代表者は存在していない.そこで,彼らはガウス分布に従っているかどうか分からない母集団について深く議論するために「区間推定」や「t分布」や「カイ2乗分布」や「ポアソン分布」などの用語が出てくる複雑な話に突入する.今回の記事のはこちらに属する話である.そしてあまり詳しくは書かなかった.

ところが物理や工業の精密測定などでは真の値を追求することに意味がある場合がある.サンプルの数がある程度大きくなるとサンプルの平均値の分布はガウス分布に近付く.そのお陰で比較的楽な議論が可能になるわけだ.

不偏分散をさらにで割ったものが出てくる.この記事ではと表現したが,特に共通の呼び名はないようである.敢えて言うなら「平均値の分布の分散に近い値」あるいはもう少しかっこよく表現すると「平均値の分散の期待値」である.

このの平方根を取れば,「平均値の標準偏差の期待値」である.この記事ではと表現した.平均値はガウス分布に従うので,ガウス分布で使っている標準偏差の記号と同じにしておいた.平均値(mean)の頭文字を付けて σ_m と書く場合もある.

これを「平均値の平均2乗誤差」と呼ぶのは,少しややこしい表現だが,そういう,素人を相手にして煙に巻く感じが少しカッコイイかもしれない.「平均2乗誤差」というのは誤差を2乗しながら足し合わせて平均を取ったものの平方根だから,だいたい標準偏差に似た概念であろう.標準偏差の別名だと思ってもらってもいい.平均値の標準偏差・・・,確かに結果的にニュアンスとしては間違っていない.しかし今回これを求めるのに使った計算過程とは少し違いがある.

予告

理論の背景をもっと詳しく数式で説明する予定だったが,既に長くなりすぎているので次回に回すことにしよう.あまり興味がない人にとっては今回の話で十分だろう.それに,記事を分けることで記号の重複を防ぐことが出来る.今回使った記号を数式中では別の意味で使ったり,式変形をすっきり見せるために別の記号を使ったりもしたいのだ.

説明不足だと感じているのは以下の 3 つに関してである.

「なぜ不偏分散を求めるのにではなく n-1 で割っているのか」
「なぜ不偏分散をさらにで割ったものの期待値が,平均値の分散になるのか」
「平均値の分散は期待値だから無数に実験しないと正しい値にならないはずなのに,なぜ回の測定だけで計算した値をそこまで信用できるのか」

いずれも入門書では軽くごまかして省略されるような話であろう.