物理数学：群速度

うなり

波の重ね合わせについて話しておこう.この話を「物理数学」の中に入れるのも少し変だが,波を重ね合わせる話は物理の色んな分野に出てくるので,どこに分類すべきか迷った末のことである.必要になったときに思い出してじっくり読み返してもらったら良いだろう.

周波数の異なる複数の波を重ね合わせると,うなりを生じる.これは高校の物理でもやる.ある一定の周波数の音のボリュームが大きくなったり小さくなったりを繰り返して,「ウワーン,ウワーン」と聞こえるわけだ.ちょっと不快だったりする場合もある.この時,波の形は次のようになっている.

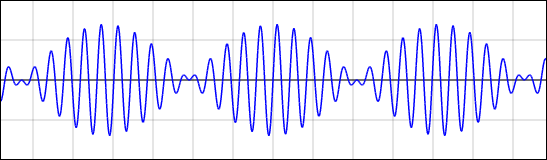
なぜこのようになるかは,次のように三角関数の和積公式を使えば理解できる. 重ね合わせた二つの波の「平均の周波数の音」のボリュームが, $cos(2π (f_{1}-f_{2})/2 t)$ というタイミングで,大きくなったり小さくなったりすることが分かる.先ほどの図に cos 関数の波を重ねて書くと次のようになっている.

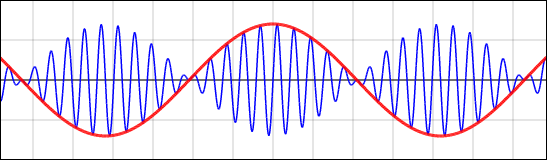
例えば 440 Hz の音と 442 Hz の音を重ね合わせると,441 Hz の音が 1 秒に 1 回の繰り返しで振動することになる.ところが cos 関数は 1 周期の中にプラスとマイナスの二つのピークを持ち,そのどちらの時でも大きく聞こえる.だから 1 秒に 2 回の割合で「ウワンウワンウワン・・・・」と激しく変化する音が聞こえることになる.

結局, $(f_{1}-f_{2})/2$ の 2 倍のテンポで音の強弱が繰り返すことになるので,公式丸暗記的な高校物理では「うなりの周波数は $f_{1}-f_{2}$ だと覚えておけばいい」という結論になるのである.

AM変調との違い

さて,ラジオの原理を知っている人は上の図の波形を見て,AM変調を思い出すかもしれない.AMラジオの電波というのは例えば 1332 kHz（東海ラジオ）などのような高い周波数を持つのであるが,それに対して音声のような 20 Hz ～ 20kHz の低い周波数の振動を重ね合わせて電波の振幅を揺らしてやることで,音声信号を電波に乗せて遠方まで伝えているのである.

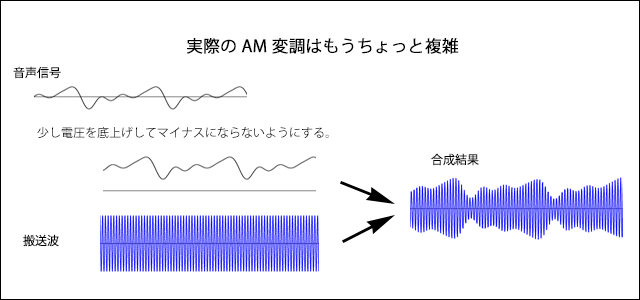
しかしラジオのAM変調がうなりと違うのは,ラジオは音声信号と電波の信号を「掛け合わせて」いるのであり,うなりの場合には「足し合わせて」いるというところである.最初に説明した「うなり」では,足し合わせた結果として元とは違う何らかの二つの波が掛け合わさった形になって見えるのであり,それでAM変調の説明図に似ているのである.

なぜここでAM変調の話をしたかというと,後でこれと絡めた話を用意しているからだ.

ところで,ラジオやテレビでは「スーパーヘテロダイン方式」と呼ばれる特別な回路が使われていることがある.そこでは周波数の異なる二つの波を重ね合わせて,結果として $f_{1}+f_{2}$ と $f_{1}-f_{2}$ という和と差の周波数を持つ二つの波を作り出し,一方だけを選んで増幅するということを行うのである.その方式の利点はさておき,これは,波を重ね合わせると言っても,「足し算」ではなく「掛け算」を行っているのであり,(1) 式のような三角関数の「和積の公式」ではなく「積和の公式」を利用していることになる.} 私は高校で波の足し合わせによって発生する「うなり」を学ぶより前にこういった電子回路で発生する「うなり」の知識を独学で知っていたのだった.どちらの場合も「うなり」と呼ばれるのである.そういうわけで,波の重ね合わせと言えば掛け合わせるものだというイメージがごく自然なものとして身についてしまっていたのだった.高校物理でうなりを学んだ後でさえそのイメージは修正されることなく,波を重ね合わせれば,当然,和と差の周波数の波が発生するものだと誤解したままになってしまった.波の重ね合わせに「足し算」的なものと「掛け算」的なものの二通りがあるということがまるで意識できていなかったのである.それで,「なぜ高校では $f_{1}+f_{2}$ の周波数を持つうなりも同時に発生することを習わないのだろう」とイライラしていたわけだが,これは生半可な知識が産んだ喜悲劇というものだ.ラジオの回路での「掛け算的な」波の重ね合わせも,音波の「足し算的な」重ね合わせも,ちゃんと数式を使って違いを理解していれば,そのような誤解をせずに済んだのに・・・と思うのである.

豆知識：ここまで「周波数」という言葉を使ってきたが,物理では同じものを「振動数」と呼ぶことが多い.英語で言えばどちらも frequency であり,区別はない.電気工学では「周波数」という用語を好んで使い,物理系では「振動数」を好んで使うという傾向がある.
しかし私は子供の頃から電気工学に親しんだせいで,電波や音波や電気信号の話をする時には周波数という言葉を使わないと違和感がある.今回の話もここまでのところは音波や電波の話ばかりだったので敢えて「周波数」の方を使ってきた.しかしここから先は電波や音波に限らない話が多くなるし,物理の解説記事でもあるのでなるべく「振動数」の方を使うことにしようと思う.

異なる速度の波の重ね合わせ

さて,空気中を伝わる音波や,真空中を伝わる電磁波の場合であれば話はこれで終わりである.なぜなら,これらの現象では,波の伝わる速さは波長や振動数には関係ないからだ.波の形についての単純な話に過ぎない.

ところが,ガラスの中を伝わる光や金属中を伝わる音波のように,振動数によって波の伝わる速度が異なるという場合がある.つまり,振動数の異なる波を重ね合わせてやった場合,それらの速度差によって時々刻々と重ね合わさり方がずれていき,全体としては波形が変化しながら進むということが起こるのである.

この波形が変化する様子の奇妙さは,止まった図を見てもらってもうまく伝わらない気がする.そこでまず,次のようなデモを用意したのでしばらくの間,遊んできてもらうことにしよう.色んなことを発見してきてもらいたい.

試してもらえただろうか？一体どんなことが起こっているのかを式で説明してみよう.異なる波長,異なる振動数を持つ二つの波を足し算で合成してみる.先ほどと同じ「和積の公式」を利用するのである. 波長や振動数ではなく,代わりに波数と角振動数を使っているのは,動く波を数式で表す場合にはこうする方が最もシンプルに表せるからだ.初学者はこれらの表記に困惑するかも知れないが,慣れればどうってことはない.それぞれは次のように定義されている. ただの変数の置き換えだと思ってもらえればいいだろう.さあこの計算結果から何が読み取れるだろう？

まず,合成前の 2 つの波,つまり (2) 式の左辺について考えてみようか.波の速度というのは ω/k で計算できる.なぜなら, という関係になっているからである.だから (2) 式の左辺の第 1 項の波の速度は $ω_{1}/k_{1}$ であり,第 2 項の波の速度は $ω_{2}/k_{2}$ であることが言える.

次に合成後の波形,つまり (2) 式の右辺について見てみよう.「二つの波を掛け合わせた」形になるという点は先ほどと同じだ.しかしこの状況を分かりやすく説明するにはどういう言葉で表したらいいだろう？「合成前の二つの波」の「平均の振動数」の波と,「差の半分の振動数」の波とが掛け合わされて重なっている.波数についても同様のことが言える.

もし波数ではなく波長を使っていたら,もっと面倒な表現をしないといけなかっただろう.とにかく波長の平均ではなく,波数の平均を取ったような波が見られるわけだ.

合成後に見えてくる二つの波は,それぞれ別々の速さで移動している.それらを求めるのは難しくはない.(2) 式の右辺の最初にある sin 波の速度は, $(ω_{1}+ω_{1})/(k_{1}+k_{1})$ だし,その後ろにある cos 波の速度は $(ω_{2}-ω_{2})/(k_{2}-k_{2})$ である.

結局のところ,速度の違う波を重ね合わせたときに起こるのは,たったそれだけの話なのだ.ところが人間というやつは,このような数式で表されたものが実際に動く様子を目にすると,数式から感じる以上の何かを見てしまう.そしてもう少し別の角度からも深く知りたいと思ったりする.

ところで,先ほどの動くデモでは (2) 式のような計算式は使っていない.愚直に足し合わせた結果を表示しているだけである.

とりあえずまとめよう.起きていること自体は単純そのものだ.だってそうだろう？波長の異なる波を重ね合わせれば,場所によって強め合う所と弱め合う所が出来る.それで波に瘤（こぶ）ができる.その重ね合わせ方をずらせば,その瘤が移動する.場合によってはほんの少しずらしただけで瘤が大きく移動したりもする.今は二つの波の速度が違っているのだから,ずらし方を常に変えているようなものだ.瘤は予想外の素早い速度で移動することもあるし,逆に非常にゆっくり移動することもあるし,二つの波の進行方向が同じであっても,それらに対して逆行することすらある.

状況を限定して考える

(2) 式というのは 2 つの波を重ね合わせた時に起こりうる全ての状況をまとめて表してしまっているので,分かりやすくもあるし,ある意味では分かりにくくもある.もっと状況を限定して,現実の現象で起こりそうなことを考えてみよう.

現実の媒質中を伝わる波では振動数によって波の速度が違うということがあり, v(f) と表せる.この場合でも振動数と波長と速度の関係は v=fλ と書けることに変わりはないから,次のように書き表せる. この辺りのことは専門書では波数や角振動数で表すことが多いから,慣れてもらうために書き直そう. 要するに,はによって表される形になっていることになる.それを k(ω) と表しても良いが,逆に解けばはで表される形になっているとも言えるので ω(k) と表してもいい.結局,波長か振動数のどちらかが決まればもう一方も決まり,それで波長と振動数の両方が決まることになるから,そこから波の伝わる速度が決まるという関係になっている.

このように,関数 ω(k) の形が具体的に分かれば,振動数に応じて波の速度が幾つになるかを知ることができる.との関係を表した式のことを「分散関係」と呼ぶ.なぜ分散と呼ぶかと言えば,これはプリズムに差し込んだ白色光が多色の光に分散することに由来しているのである.このプリズム現象はガラス中を伝わる電磁波が波長ごとに速度が違うせいで起こるのであり,その現象についても ω(k) という形で表すことができる.その関数の具体的な形は少し複雑になるので,また別の機会にどこかで説明することにしよう.

振動数が幾つであっても波の速度が変わらない場合には ω=ck という関係になっており,この定数が波の速度である. ω(k) が ω=ck 以外の形をしている場合には波長や振動数によって波の速度が違っており,それを「分散がある」と表現する.

ではここからが本題だ.波長がごくわずかに違う二つの波を重ね合わせてみよう.いや,波長で考えると式がややこしくなるので,波数で考えることにする.一方の波の波数がであったとして,もう一方が k+Δk だったとする.すると角振動数の方も一方が ω(k) であったとすると,もう一方は ω(k+Δk) であるわけだ.このというのは次のように近似することができる. 以上のパラメータを (2) 式の右辺に当てはめてみよう. sin 波の波数と角振動数はほとんどとだと考えてよい.一方, cos 波の方は波数が 1/2 Δk で,角振動数が 1/2 dω/dk Δk である.波数から判断すれば, sin 波の方は小刻みに振動し, cos 波は緩やかに,長い波長でうねるように見える.では波の速度を計算してみよう. sin 波の方は計算するまでもなく ω/k であり, cos 波の移動速度はを 1/2 Δk で割ればいいので, dω/dk であることが分かる.

sin 波の移動する速さを「位相速度」と呼び,包絡線になっている cos 波の移動する速さの方を「群速度」と呼ぶ.もう一度繰り返すが,位相速度は ω/k であり,群速度は dω/dk であるということである.

なぜ位相速度と呼ばれているかについてはあまり深く考えない方がいいかも知れない.この波が移動する様子を見ていれば,包絡線に包まれた内部で,波の細かい山や谷が包絡線の移動速度（群速度）とは関係なく移動しており,いかにも「波の位相の変化を図で表したもの」が動いている感じではないか.いや,大したことは言ってないので分からなければ無視してくれていいよ.

補足：バカらしいことに言葉を費やすのがもったいないのでついつい説明を省きたくなるが,詳しく説明すれば分かってもらえるかも知れないので,もう少し努力しておこう.例えば sinθ をグラフに描いたとする.この場合,位相というのはθのことで,「位相の変化を図で表したもの」とは sinθ のグラフのことである.その波形が移動する速度だから「位相速度」である.たったそれだけのことかよ！って？気持ちは分かる.多分,たったそれだけのことだ.

豆知識：物理学者や工学者は phase を位相と訳し,数学者は topology を位相と訳した.それでしばしば混乱が生まれている.数学用語に慣れた人が物理に接すると「これのどこが位相だよ！」と怒ったりする.おまけに数学には「位相空間(topological space)」という専門用語があり,物理にもそれとは別の意味での「位相空間(phase space)」という専門用語がある.

念のため、もう一度まとめ

群速度と位相速度について理解してもらえただろうか？波長なり,振動数なりがごくわずかに違う二つの波を重ね合わせた時,いや,わずかに違うと言ってもほとんど同じであり,どちらの波もだいたい ω/k で進んでいたわけだ.それらの合成後の波には瘤（こぶ）のような振幅の変化が付くことになるのだが,その瘤のデコボコを無視すれば,やはり ω/k で進む波が見えており,それが位相速度である.

一方,その瘤のような包絡線も移動するのであるが,その速度が群速度である.群速度は,元々の二つの波のわずかな速度差に大きく影響を受ける.だから,元々の二つの波の波長や振動数がわずかに異なるときに,どの程度の速度差が出るかが重要である.それで dω/ dk という量が関係してくるのである.

ω/k と dω/ dk は形は似ているが,位相速度や群速度がこのように表されることになった由来,その意味合いが全然違うわけだ！

もし分散関係が ω=ck という形で表されている場合,それはどんな振動数,どんな波長の波も同じ速度で進むことを意味している.この場合でも振動数の異なる波を重ね合わせれば瘤はできるが,位相速度と群速度に違いはない.つまり,重なり合った波形が,そのままの形で,ずっと同じように進むことになる.

群速度は光速を超えない

さて,いよいよ「群速度」と「位相速度」を理解する上での最後の試練である.

今までにどこかで次のような話を聞いたことがあるかも知れないし,今後どこかで聞くことがあるかも知れない.「位相速度は見かけの速度なので光速を超えることがあってもいいけれども,エネルギーや情報を伝えるのは群速度なので,群速度が光速を超えることはない」というのである.

ちょっと待て,本当かい,おい！？

この話は群速度を理解したと思っていた頭に混乱を招く.むしろ逆ではないのか,とさえ思える.群速度は,もともとの合成前の波が持っていた速さとは異なる速さで動くのだった.ずっと素早く移動することもあるし,止まっているかのように振る舞うことすらある.それぞれ単独でも存在しうる波を重ね合わせることで生じた瘤の移動なのだから,見かけの存在であるのは群速度の方ではないか,と思ってしまうのである.

この話はプラズマ中を伝わる電磁波の速度を計算した時に特に問題になる.なんと,それは必ず真空中の光速よりも速くなるという結果が出るのだ.しかしその分散関係 ω(k) を使って群速度を計算してやると必ず光速よりも遅いという結果になる.さて,実際には何が起きるというのだろう.

真空中からプラズマ中へと差し掛かった電磁波は,まるで抵抗を受けるかのように急減速がかかり,波形が乱れる.その乱れた波形の中に,超光速で動くかのような波が観察されるが,それは波の先頭にまで達する以前に振幅が小さくなり消えてしまう.結局は,電磁波が伝わってきているという情報は,光速以下で伝わる大きなうねりより先へは伝わらないのである.このことを「先端速度は光速を超えない」と表現することがある.

ところが,このような最初の突入時のうねりが終わってしまった後で振幅が一定に落ち着くと,やはり超光速で波が進んでいるかのように振る舞う.そのため,実際にプラズマの屈折率は 1 より小さな値を取り,凸レンズ型をしたプラズマに電磁波が突入すると,それは焦点を結ぶどころか,逆にまるで凹レンズが光を広げてしまうのと同じように振る舞うのである.

この状態に達してしまうと,やはり電磁波はプラズマ中を超光速で進んでいるように見える.しかしこの状態から少し振幅の値を変化させてやったらどうなるだろう？その変化は新たなうねりを生じ,そのうねりは光速以下で伝わるのである.結局,振幅を変化させたという情報は光速以上では伝わりはしない.

これ以上プラズマについての詳しい説明はしていられないが,最初の方の説明との折り合いは付けておかなくてはならないだろう.実は,最初の方からしてきた説明には少しばかり反省点がある.理想を語っており,現実が無視されているのである.

ここまでの説明で出て来た「重ね合わせる以前の二つの波」というのは理論の上だけのものであり,それは空間の端から端まで終わりなく一定の振幅で続くような存在である.我々はそのようなものを想像の上で動かすことは出来ても,現実には自由に操ることはできない.我々が発生させる現実の波には必ず初めと終わりがあるし,振幅を途中で変化させたりもする.

一定の振幅のまま無限の彼方まで続いている波は,エネルギーも情報も運ぶことはできない.そのような波はエネルギーを持っているかも知れないが,そのエネルギーはすでに全空間に行き届いており,未来永劫一定なのである.情報やエネルギーを新たに運ぶためには,そのような波を出すのをやめたり,再び発生させてみたり,あるいは振幅を変えてやることで,その振幅の変化が伝わるようにしないといけない.

我々が普通の波だと考えて,新たに発生させたり振幅を変えたりすることで情報やエネルギーを乗せている波というのは,最初の方で話したラジオの AM 変調のようなものである.それは「掛け合わせ」て作られたかのような形をしているが,三角関数の積和の公式を使ってやれば,振幅一定の波を「足し合わせ」て作った波として解釈することも可能である.より複雑な波形の場合には,今回のような二つだけの波の重ね合わせでは作ることはできず,フーリエ解析でやったように多数の波の重ね合わせを考えて実現することになるのだが,今回は基本的な考えだけにしておこう.とにかくそのような理屈になっており,我々が波に乗せた情報やエネルギーは全て群速度で移動することになるのである.これが,位相速度が光速を超えていても群速度が光速を超えていない限りは問題ないと言える理由である.

真空中の電磁波や音波を使う限りは位相速度と群速度は同じなので,このようなことは意識しないで済んでいる.

群速度は光速を超えてもいい

ところがだ,今説明したのとは全く逆に聞こえる話を聞くこともある.「位相速度は光速を超えることはないが,群速度は見かけの速度なので光速を超えることがあってもいい」というのである.実はこれも正しい.しかし先ほどとはまた違った前提での話である.

近頃はナノテクノロジーが発展してきており,人工的な構造をもつ結晶が作成できるようになってきた.光の伝わり方についてかなり変わった性質をあれこれと持たせることもでき,そのようなものは「フォトニック結晶」と呼ばれている.分散関係 ω(k) を割りと望み通りにデザインできるようにもなってきた.

そのような材質で作った光ファイバーなどに波長の異なる複数の光を重ねて通してやると,群速度が真空中の光速を超えて進むような波形を作ることができたりする.もっと多数の光を重ねてやれば,かなり複雑な波形も合成できるわけで,まるで鋭いパルスが一定時間ごとに光ファイバーの中を超光速で駆け抜けるように見せたりもできるわけだ.

同じような理屈で,まるでパルスが空間に停止しているように見せることさえもできる.時々「結晶中で光を止めることに成功！」などという驚きの見出しで出てくる科学ニュースはこの類だ.

このような場合の群速度は情報もエネルギーも運んではいない.見せかけのものだ.実際には光速以下で進む一定の振幅の多数の波長の波が光ファイバーの端から端まで進み続けているだけであり,それらの重ね合わせによって合成された図形によるアニメーションを見ているようなものである.

結局はどういうことなのか

結局のところ,群速度は光速を超えてもいいのか,いけないのか？そのように問うてみると,自分でここまで書いたにもかかわらず分からなくなってきてしまった.多分,質問の仕方が良くないのだろう.

我々の扱う,エネルギーや情報を伝える波は光速を超えることがない.そのような波は全て群速度として表される.その形を波長ごとに分解してやると,理論の上では超光速の波が現れることもあるかも知れないが,振幅の変化のない波であり,エネルギーや情報を伝えるものではない.「そういうものの重ね合わせで出来ていると解釈することもできる」というレベルの仮想上の存在だ.

一方,結晶の内部のように限定された範囲のみを考えれば,我々は端から端まで一定振幅の波でその範囲を満たすことができる.そのような波を重ね合わせることで波の塊を作り出し,群速度をある程度操ることができる.その波の塊はただの重ね合わされた結果を見ているだけであり,エネルギーや情報を伝えるものではない.

つまり,我々の作る波のうち,エネルギーや情報を載せたような形のものは全宇宙を考えれば全て群速度として理解できる.群速度だから光速以下でなければならないのではなく,たまたま別の物理的な要請によって,それが光速以下でなければならないだけの話だ.しかし限定された範囲だけに注目するなら,一定の振幅で移動する理論的な理想に近い波を我々は用意できて,それらを重ねて作った波の塊が群速度で移動するのを観察することができる.このようにして作った群速度には物理的な速度制限はない.結局のところ,光より速いかどうかは群速度であるかどうかには全く関係のないことなのだ.

何度も同じことを繰り返してるだけのようにも思えてきたが,ようやくスッキリしてきた.