物理数学：複素微分

複素関数

微分の概念を複素数の範囲にまで拡張してやりたい.というか,さっさと微分の話をしたい.その為にはまず関数が必要だ.なぜ必要か？高校の範囲の数学では,変数が実数であるような関数 f(x) を用意して,「 f(x) をで微分する」というような表現をしたのだった.同じようなことをしたいのである.だからまず,関数を複素数の領域にまで拡張することから考えよう.

何も難しいことはない.複素数に対して複素数の範囲で値を返すような関数 f(z) を考える.ただそれだけである.この関数 f(z) のことを「複素関数」と呼ぶ.ここで変数をとは書かないでという記号で表しているのは,これが実数ではなく複素数であることを強調するためであって,色んな教科書がその書き方を採用している.本当はどんな記号で表わしてもいいのだが, f(z) と書かれたものを見ると「おそらくこれは複素関数の話をしてるのだろうな」と一目で想像が付くという利点がある.高校までに習った実数の範囲の関数を複素関数と区別するために「実関数」と呼ぶことにしよう.

変数と値の間にどんな奇妙で複雑な対応を考えてもいいのだが,定義が場合分けだらけだったりして至る所で不連続だという関数では微分ができない.せめて有限個の点を除いては連続であってほしい.それは実関数の場合にもそうだった.例えば, というようなものも関数の一種ではあるのだが,こういうひねくれた関数は扱いたくないのである.そういうわけで,比較的行儀の良い,分かりやすい規則がある関数だけを例として色々と挙げてみよう. これは入れた複素数値をそのまま返すという極めて単純なものだ.もう少し複雑なものを考えた方が面白いだろう. これは実関数でもよく見るような「いかにも関数」という形である.しかし複素数の範囲で値を代入してもちゃんと計算して値を返すことができる.すでに複素数の和や積の方法については説明してあるからだ.ここでは係数がどれも実数になっているが,係数を複素数にしてもいいだろう.例えば次のような具合だ. もう少し変わった形のものも欲しい. これは z=0 の時にだけは定義できないが,それ以外の点では連続な関数だろう.有限個の点を除いては連続で,ちゃんと計算して値を返すことが出来ればいい,という要望に沿ったものならば,次のようなものでもいいだろう. これは複素数に対してその複素共役を返すという関数だ.こういう形が許されるなら,の実数部分だけを返すという関数だって作れそうだ. この調子でいけば,ひねくれたものが他にも色々と作れそうだぞ.結果を計算できて値を返すことができりゃいいというんだろう？実部と虚部を入れ替えて返す関数だとか,そうだな,それだけじゃ物足りない.こんなのはどうだ？実部と虚部を分けて,それぞれに計算して,その結果を合わせるといった感じである.思い付きでテキトーに作っただけで,特にトリックなどはない.

うーん,なんだかなぁ・・・.実関数ではちょっと思い付かなかったくらい自由すぎるではないか.こんな状況に付き合って行けるのかと心配になってくる.

しかしまぁ,安心して見ていてほしい.妙な振る舞いをする面倒な関数はこの後の議論では扱わなくても良くなってくる.というより,扱えなくなってくるのである.これからちょっとふるいに掛けてやることにしよう.

微分の定義

高校で習ったはずの実関数の微分の定義はちゃんと頭に入っているだろうか？現状ではこういうことを軽視していても受験を通過できてしまうので,ここでもう一度説明しておかないと不安である. 変数の値がからごくわずかに変化して x+h になったとき,関数 f(x) の値もごくわずかに変化して f(x+h) になる.つまり,変数がだけ変化するとき,関数は f(x+h)-f(x) だけ変化するわけだ.この両者の変化の比を知りたいのだが,としてどれくらいの大きさを考えるかによって値が違ってくる.そこで,が限りなく 0 に近付いたときにどんな値に近付くかを考える.それこそが関数 f(x) を微分した f'(x) の意味である.その f'(x) の値はその各点,各点での関数 f(x) の変化率を意味している.関数 f(x) をグラフにしたときの曲線の傾きを意味していると言ってもいい.

さて,形式的にはこれと全く同じものを複素関数の微分の定義として採用しよう. 変数と書いてあったところを複素数の変数に置き換えただけだ.いや,それ以外にもう一つ重要な変更がある.わずかな変化も複素数だと考えるところである.このことで何か変わったことが起こるだろうか？

話をもう一度,実関数の方へ戻してみよう. f'(x) は関数のグラフの傾きを表していたから,これに変数の微小な変化を掛けることで関数の値のおおよその変化を予想することができる.つまり,次のような式が成り立っているということだ. この時,微小変化はプラスの値だとは限らない.もしマイナスの値であった場合にもこの関係式が成り立っていて欲しい.それは言い換えれば,ある点から右へ進んだ場合にも左に進んだ場合にも関数の傾きが同じであってほしいという自然な要求である.もしそれが満たされていないと次の図のようなことになる.

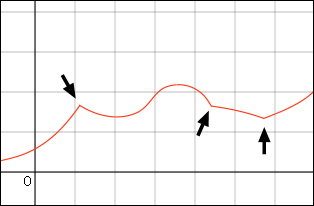
この図では,幾つかの場所で,右へ進むときと左へ進む時とでグラフの傾きが違うということが起きている.グラフが折れている場所,「その一点」での関数の傾きは一体幾つなのだ,と問われると,答えることが出来ない.こういう幾つかの点ではたとえグラフが連続であっても「微分可能ではない」と言われる決まりだった.

これと同じようなことを複素関数の微分に於いても要求してやろうではないか.式で書くとこうだ. (1) 式とほとんど同じだが,微小な変化として複素数を考えているという点で大きく違う.実数の場合には,グラフを右向きに進むか,左向きに進むかだけを考えれば良かったが,複素数というのは平面上に表せる数だったから,あらゆる向きを考えないといけない.どんな方向へ変化した場合にもこの式が成り立っているべきだ,という厳しい条件を課してやるのである.よっぽどの偶然が重ならない限り,そんなうまいことが起きるとも思えないのだが・・・.

ではこれから,どんな時にその厳しい条件が満たされることになるのかを調べてやろうではないか.

コーシー・リーマンの関係式

条件を求めるための頼りは (2) 式なのだが,実部と虚部が分かれていない書き方になっているのでこのままでは状況の把握が難しい.そこで,徹底的に実部と虚部を分けた書き方に直してみよう.

まずは変数を次のように書き換える. 本当は今まで使ってきた形に合わせて z=a+bi と書きたいくらいなのだが,我々はやという記号に対してはあたかも定数を表すかのようなイメージを強く持ってしまっている.記号のイメージが思考を縛ることはよく起こるのだ.今はは変数であるから,その実部も虚部も変数である.よって変数のイメージが強いやを使うことにする.

次に, f(z) についても実部と虚部を分けて次のように表してやる. なるほど,複素関数は 2 つの 2 変数関数から出来ていると解釈できるわけだ.

微小変化はどう表すべきか.あまり記号を増やしてもごちゃごちゃして論理を追いきれなくなるだけだ.ここはいかにも微小変化らしく,次のようにしておこう. さあ,残るは f'(z) である. f(z) については先ほど, u(x,y) と v(x,y) を使って表したのだった.しかしこれにならって f'(z) = u'(x,y) + iv'(x,y) などと表示するわけには行かないのである. u'(x,y) と書けばあたかも関数 u(x,y) の微分みたいに見えてしまうからだ. u(x,y) は 2 変数関数でもあるし,多変数関数の微分はそんなに単純なものではない.それに我々はまだ f'(z) の具体的な計算方法を十分に検討していないのであり, u(x,y) や v(x,y) との関係もよく分かっていない.そこで単純に次のように表しておくことにしよう. 先ほどやはあたかも定数であるかのようなイメージなので使用を避けたいと書いた.しかしそれを敢えてここで使うのには,一つの気持ちが込められている. f'(z) の値が,の方向によって様々な異なる値を持つのではなく,ある一点では一つの値に定まって欲しいという気持ちである.それでいかにも定数っぽい記号を使うことにしたわけだ.

f'(z) は変数の関数として決まるはずのものなので,ここでのやも本当は変数との関数である.しかし,ごちゃごちゃしないように敢えて a(x,y) などとは書かないようにしている.

これで準備は整った.これらの記号を使って (2) 式の置き換えを実行しようではないか.次のような具合になる. 右辺の最後の項の積を展開するとこうなる. 左辺の実部と右辺の実部,左辺の虚部と右辺の虚部がそれぞれ等しくなっているはずなので,この式は次の二つの式に分離することができる. 意外と単純な式に見えるだろう.もし読者がすでに多変数関数の微分の話を知っていれば,ここでピンと来るはずなのである.ピンと来ない人は先に多変数関数の微分について学んでくるか,分かったフリをして次の話を受け入れるかのどちらかを選択して欲しい.

要するに,多変数関数については (3) 式や (4) 式に似た次のような関係式がある,という知識さえあればいいのである.ここでは多変数関数を g(x,y) として書いておこう. ここで, ∂g/∂x のように書いてあるのは「偏微分」の記号である.難しいことではない.は関数 g(x,y) のうちの以外の変数には目もくれないで,つまり変数を単なる定数であるかのようにみなして,で微分するという意味である.一方, ∂g/∂y は変数の方を定数だとみなしてで微分するという意味である.

この (5) 式の g(x,y) の部分を u(x,y) に置き換えて考えれば,(3) 式から次のことが結論できる. また,(5) 式の g(x,y) を v(x,y) に置き換えて考えれば,(4) 式から次のことが結論できる. そしてやが複素平面上のある地点においてはただ一つの値しか取らないのであれば,(6) 式と (7) 式を組み合わせた次の関係が言えるはずである. この二つの式を「コーシー・リーマンの関係式」と呼ぶ.これこそが (2) 式が成り立つための条件,すなわち探し求めていたものの形である.

正則な関数

今導き出した条件を使って,一体どんな形の関数が「微分可能な複素関数」として認められることになるのかを確かめてみよう.

ここまでの話をもう一度自分自身で考え直している賢明な読者は次のような疑問に突き当たるかも知れない.なぜコーシー・リーマンの関係式で微分可能かどうかを判定できるのだろうか.果たして実関数の場合には微分可能かどうかを確かめるための同様な公式はあっただろうか,と.そんなものはないというのが答えだ.コーシー・リーマンの関係式を適用するためには,それ以前に実関数である u(x,y) や v(x,y) が偏微分可能でなくてはならない.まずその条件をクリアすることが必要で,これが実関数の場合の微分可能の条件に相当している.複素関数の場合には,その上にさらに条件が課せられて,それがコーシー・リーマンの関係式だというわけだ.

さっきから微分可能という表現を多用しているが,実は複素関数を扱う場合には「微分可能」という表現を使わない習慣になっている.微分可能であることの条件がこんなにも厳しいので,元々の「微分可能」という言葉のニュアンスから離れてしまっているからだろう.代わりに「微分可能な複素関数」のことを「正則な関数」と呼ぶ.

注意：厳密さが必要でない分野では「微分可能」と「正則」を区別せずに使うことが多いが厳密な議論が必要なときはこの二つの概念は別のものとして区別される.微分可能とはある点 z₀ においてコーシー・リーマンの関係を満たすことであり,正則とはある点 z₀ とその近傍でコーシー・リーマンの関係を満たすことである.例えば f(z) = |z|² という関数は z=0 の一点においてコーシー・リーマンの関係を満たすので微分可能だが,ここから少しでも離れるとコーシー・リーマンの関係を満たさない.つまり f(z) =|z|² は z=0 において微分可能だが正則ではないということになる.
実用上はなぜこのような区別が必要ないかと言えば,一点のみで微分可能であるような関数には全く関心がないからである.

では表現を改めて,もういちど仕切り直し.さあ,これから正則な関数の具体例を探そう！

最初の方に挙げた複素関数の例を順次コーシー・リーマンの条件に当てはめて確認してみようか.だとすれば,まずは最も簡単な例としての f(z)=z からだ. z=x+iy とすると, f(z)=x+iy だから, u(x,y) と v(x,y) はそれぞれ, だということになる.これはコーシー・リーマンの関係を満たしている.よって, f(z)=z は複素平面の全域で正則だ.意外と簡単に一つ見つかったな.しかしもう少し複雑になったらどうだろう？

前の例には挙げなかったが,少しだけ複雑な例として f(z)=z^2 というものを考えてみよう.これはなので, であり,やはりコーシー・リーマンの関係を満たしている！なんだ,厳しい条件だと思ったが,簡単に幾つでも見つかりそうではないか？

とにかく,こんな具合に試していくのである.

ところがだ,こういうことを繰り返しているうちに,毎回このような検証をしなくても楽に判別の付くパターンがあるのが見えてくる.関数 f(z) と g(z) がともに正則ならば, f(z)+g(z) も f(z)-g(z) も正則だ,とか,そういう類の法則だ.他にも,関数 f(z) が正則ならばそれを複素数倍した af(z) も正則だとも言えそうだ.ちょっと考えてみてほしい.いずれもコーシー・リーマンの関係式を満たしているだろう.

いや待てよ？その辺りの内容ならわざわざコーシー・リーマンの関係式を使って考えなくても,微分の定義の形から直接に証明可能ではなかろうか.実関数の微分の定義と形式が全く同じなので,実関数の場合に導いたのと同じやり方で次のようなことが言えてしまう. 高校数学の範囲でできることなのでここでわざわざ証明するのはやめよう.とにかく関数 f(z) と g(z) がともに正則であれば,微分の結果はこれらの式の右辺のようにして計算されて,ただ一つに定まることが言える.つまり左辺のカッコの中の形に書かれる形式の関数は微分の値が定まるので正則だということだ.

ということは,今のところ,次のような形の関数は全て正則だということになる. z≠0 であればこういう形のものでも良さそうだ. 合成関数も許されているので,次のようなものでもいいだろう. ただしこの場合は z=5i を除く点で正則だということになるだろう.

このような単純な形の関数ならば,微分を計算するのも簡単だ.実関数でおなじみの次のような公式が使える. 複素関数の微分の定義式が実関数の場合と同じ形式になっているので,まったく同じ手順で導かれるのである.

「微分可能」の条件が実関数の場合よりはるかに厳しいにもかかわらず,コーシー・リーマンの条件を満たす関数のバリエーションはかなり多いことが分かる.そして実関数のときと同じ計算方法がそのまま使えるというのだ.

正則でない関数

さっきから正則な関数ばかりである.どんな関数が正則でないかという話もしておかないと全体像がつかめない.色々と紹介してみよう.

例えば,最初の方に出てきた $f(z)=z^{*}$ という関数は正則ではないのだ.なぜなら, z=x+iy だとすると $f(z) = z^{*} = x-iy$ だから, であって,コーシー・リーマンの関係式を満たさない.なぜこれが正則ではないかについての直観的な説明が欲しいかも知れない.が実数方向へ進む時には関数の値も同じように実数の値が変化するからあたかも「傾き」が 1 だけれども,虚数方向へ変化するときにはプラスマイナスが逆転しているので「傾き」が -1 になる.そういう違いが出ることが受け入れられない原因なわけだ.ここで言う「傾き」というのは実関数のグラフに倣ったたとえの表現に過ぎないのだけれども.

実数部分だけを取り出す関数 f(z)=Re(z) というのも同じように受け入れられない.を実数方向へ移動した場合には関数の値に変化があるが,虚数方向に移動しても関数の値には全く変化がないということになるからだ.わざわざ u(x,y) や v(x,y) を求めて確かめるまでもない.

絶対値を対応させる関数 f(z)=|z| ではどうだろう？今の例とは違って,が実数方向へ進んでも,虚数方向に進んでも,関数の値に何らかの変化があるはずだ.まぁ,確かめてみよう. z=x+iy だとすると f(z)=√(x^2 +y^2) であるから, やはり明らかに受け入れられないな.つまり,実数方向へ進んでも虚数方向に進んでも,実数方向への変化しかないという辺りで,良くないのである.変数の変化量と変化率である f'(z) を掛けた結果が関数値の変化にならないといけないのだから,が実数でも虚数でも関数の変化分が実数にしかならないというのは明らかにおかしいわけだ.

これで正則かどうかの大体の雰囲気が分かってもらえただろうか.正則な関数というのは,変数の冪級数のようなものだとか・・・,うーんと,どう表現したら分かり易いだろう.要するに,変数を使った掛け算,割り算,足し算,引き算の組み合わせで表現できるようなものばかりなのである.

広がる可能性

こうしてまとめてしまうと,正則な関数というのはバリエーションが多いようでいて,かなり制限されているようでもある.関数というものは他にも色々と種類があるはずだ.例えば指数関数とか,対数関数とか,三角関数とか・・・.それに似た感じの不思議な性質を持つ複素関数を考えたり,微分をしたりという議論は無理なのだろうか？

いや,そんなことはない.テイラー展開というものがあって,色んな実関数を冪級数の形に表せることを学んだことがあるだろう.まだ学んでない人は先を読み進む前にどこかで学んで来て欲しい.その技術を使えば,色んな関数を冪級数で表せるので,それらも正則な関数だと言えることになりそうだ.

今までのところ,テイラー展開は実関数の範囲でのみ議論していたのだった.しかし,テイラー展開の結果として得られる冪級数の変数部分に複素数値を代入したとしたら,何が起こるだろう.変数が実軸上の値を取る限りは従来の実関数と同じ振る舞いをしつつ,変数が実軸上を飛び出しても何らかの値を返すという新しい種類の関数が出来上がりそうだ.色々な実関数が,もとの性質を保ったまま,複素平面上の変数にまで拡張されるのである！

・・・という素晴らしい展望が見えたものの,その話に入る前にもう少し議論しておかないといけないことがある.テイラー展開の結果得られる冪級数はいつでも収束するとは限らず,変数の範囲によっては無限大に発散してしまうことがあるのだった.それが複素平面上ではどうなるのかをまず知っておかないといけない.