物理数学：オイラーの公式

級数の収束

前回の終わりに,収束や発散が複素数の場合にどうなるかを論じなければならない,と脅かしたのだが,調べてみるとそんなに大した話でもなさそうだ.実数の場合の証明がほとんどそのままの形式で使えて,ほぼ同様の内容が複素平面上でも成り立つことが分かるからだ.よって,今必要な主な結果だけをざっと再確認するにとどめておこう.

まず,次のような級数を考える. この各項に絶対値を付けてという形にしても収束することを「絶対収束」と呼ぶのであった.これは,たとえ (1) 式の全ての項を絶対値に変えて正の値に統一したとしても収束するということだから,かなり厳しい条件をクリアしているということだ.(1) 式が絶対収束するならば,(1) 式は収束すると言える.ここに出てくる絶対値を複素数の絶対値に置き換えても同じことが成り立つ.

さらにもう一つ. という形の冪級数が $z=z_{0}$ にて収束するならば, $|z|<|z_{0}|$ を満たすようなあらゆる場所にて,(2) 式は絶対収束する.このことも複素平面上でそのまま成り立つというのだ.これが意味する内容をイメージしてみてほしい.そのすごさが分かるだろうか？

$z_{0}$ という値は複素平面上の原点から $|z_{0}|$ の距離にあるのだが,その値 $z_{0}$ を代入したときに (2) 式が収束することが確認されたなら,原点を中心とする半径 $|z_{0}|$ の円内にあるどの点の値を代入したときにも確実に収束するというのである.

すると,原点からどれくらい離れた範囲までなら収束するのだろうかと確認してみたくなるのが普通だろう.それで徐々に原点から遠ざかりながら調べてやる.収束が確認されるたびに,その円形の範囲が広がるわけだ.そしてついにどこかで発散する場所を見付けたとしたら,その半径の円内では確実に収束し,その外側では必ず発散するといった状況になっていると結論せざるを得ないはずだ.なんとすっきりしたイメージか！その半径のことを「収束半径」と呼ぶ.実数の場合にも同じ用語を使っていたが,複素平面上では文字通りの円の半径を意味しているわけだ.

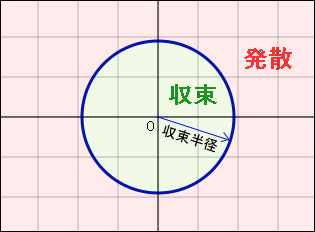
このようなことが言えるにもかかわらず,収束と発散の境界線である円周上にある点では (2) 式が収束するか発散するかについての確実な法則がない.事実,円周上のある点では発散するが円周上の別の点では収束するといったようなタイプの冪級数も存在している.個々に調べるしかない.

冪級数には複素平面上の全域のどんな値を代入しても収束するというものもあり,その場合には「収束半径は無限大」だと表現する.一方, z=0 以外の値では発散する冪級数もあり,その場合の収束半径は 0 であるとする.

収束半径が幾つになるかを調べる方法は幾つもあるが,実数の場合と全く同じである.「簡単に計算できて便利ではあるがいつでも適用できるわけではない方法」もあれば,「確実だが計算が面倒で使いにくい方法」もある.

複素平面上で使える関数の定義

さて,収束の話が割りと短くまとめられたので,さっさと次の話題に移ってしまおう.実数の範囲では指数関数や三角関数が次のようにマクローリン展開（ x=0 の周りでのテーラー展開）できるのであった. そしてこれらの収束半径は無限大であることが確認されている.すなわち実数の全域で使えるということだ.

ここで,これらの冪級数の変数に複素数の値を代入することを考えよう.先ほど話した収束半径の話から考えて,複素数を代入した場合にも収束半径は無限大である.実数は複素平面の一部だから,実数での収束半径がそのまま複素平面での収束半径になるわけだ.つまり,どんな複素数値を代入しても必ず何らかの値に収束することになる.よってこれらの式を複素平面上での新たな指数関数の定義,三角関数の定義として受け入れることにしよう. を乗するなんてことにどんな意味があるのかと考えても全くイメージが作れなくて困るわけだが,それは実数の関数をこんな具合に拡張定義したものだと説明されれば,まぁ受け入れるしかない.実際そういうものなのだ.

このような定義を採用しても, $e^{x+y}=e^x e^y$ という指数関数の基本的な性質をちゃんと受け継いでいることが分かる.ここでやはともに複素数でもいいということだ.それはやり方によっては簡単に示すこともできるが,納得の行くまで確認してみてほしい.そうすれば $e^{a+bi}=e^a e^{ib}$ のような式変形も当然のものとして受け入れられるようになるだろう.

また,三角関数についても実数の時と同じように加法定理などが成り立っている.しかしそれを確認するのはかなり面倒だろう.これについてはずっと後の方で出てくる便利な定理によって簡単に示すことができるようになるので楽しみにしていてほしい.

オイラーの公式

指数関数や三角関数のテイラー展開を並べて見比べていると,どうもそれぞれが無関係ではないような気がして仕方なかった.実際,深い関係があり,複素数の範囲で考えればそれらがうまく繋がるのだ.

今回めでたく変数が複素数にまで拡張されたことだし,指数関数の定義の式ののところにを代入してみよう. なるほど！これはの付いてる項と付いてない項に分けて次のようにまとめられるのではなかろうか！無限に続く級数の場合には項の順序を変えたりすることに慎重でなければならないのだが,今回のように絶対収束する場合にはそういう心配をしなくていいことが証明されている.要するに,今の結果はこういうことである. これが「オイラーの公式」と呼ばれる有名な式だ.今の話の流れを見る限りが実数でなければならないという制限はない.事実,この関係はに複素数を代入しても成り立つのである.しかし今はまだこの式に慣れていないと思うので,を実数の範囲に限定して考えてみよう.実数だということがはっきりするようににして書き換えておこう. ははーん,どっかで見たような式になったなぁ.覚えてるだろうか.複素数は絶対値と偏角を使って表すとのように表せるという話を複素関数論の一番最初の記事に書いたのだった.今の (3) 式を使えば,この (4) 式と同じことを次のようにも表せるということだ. これを複素数の「極座標表示」と呼ぶ.

このことから $e^{iθ}$ についての図形的イメージを描くことができる. $e^{iθ}$ は,絶対値が 1 で,偏角がであるような複素数値を表している.つまり複素平面上に,原点を中心にして半径 1 の円を描いたイメージだ.

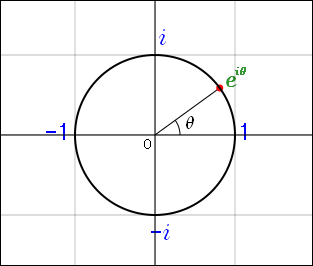
例えば,偏角が 90°つまり θ=π/2 なら $e^{iθ}$ はを意味する. また偏角が 45°つまり θ=π/4 ならこういうのは全て (3) 式を使って計算できる.

(3) 式のに円周率を代入してやると,昨今の数学ブームでよく知られることになったオイラーの等式が出来上がる. 神秘的な感じがする式なので必要以上にもてはやされているようだが,この式は複素関数論のゴールではない.最初の方の通過点というか,その近くでのちょっとした道草みたいなものだ.まだまだずっと先がある.

まぁ,この式にたどり着けたことを記念してしばらく眺めていたい人もいるだろうから,今回の話はこれくらいにしておこう.

ちょっと気をつけること

話が軽やかに進んだので,ひょっとして悩む暇もなかったのではないかと心配している.ここの話は見た目よりも入り組んでいるのである.

我々は複素平面上の値に対応できる関数を幾つか導入した.例えば,複素数値に対して複素数値 e^z を対応させるような関数だ. これはを z=a+bi のように表すとすると,それに対応する複素数値はであるという話である.

一方,後半のオイラーの公式は,そのような「複素平面に拡張された関数」を利用した応用の話である.特に極座標表示はそのものが $re^{iθ}$ という形で表せるというだけの話であり,に対して f(z) が対応するというような関数的な話ではない.

今の話でちょっと混乱を始めた人がいるかも知れないが,こういうことについて頭を整理するために長い時間を取るのは良いことだと思う.