物理数学：複素積分

イメージ

微分の話は終わったので次は積分だ.微分は簡単だったが,積分については書くことが多いのである.今回は基本だけさらっと説明してしまおう.

実数での積分をなるべく素直に拡張してみたい.しかし矛盾が生じないように気を付けないといけない.複素数の範囲で使えるように考え出した「新しい積分のやり方」を実数の範囲に制限して実行したときに,これまでの積分と同じ結果が出るようにしておきたいのである.

実数の範囲での積分はどういう考え方で作られていただろうか？まず積分する範囲を決めておき,その区間を細かく分割する.そして各点での関数の値と微小区間の長さとの積を計算すると短冊のような形の面積が多数求まることになるだろう.それらの微小な面積を全て足し合わせてやる.もし区間を無限に細かく分割してゆくことを考えれば,その合計値は次第にある一定値に近付くはずであり,そのような値がもしあれば,それを積分の値だとすると決めたのである.

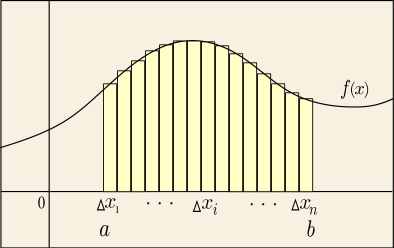
あまり正確には表現できていないが,その気持ちを式で表せばこんなものだ. さて,この考え方を出来るだけそのまま引き継ぎたい.実数の定積分では積分範囲を定めるために実軸上の 2 点を指定しさえすれば良かったのだった.しかしそれと全く同じにしては面白くない.複素関数の変数はもはや実数の一直線の上に縛られてはいないのだから,複素積分では複素平面の上を自由に動きたい.しかし自由すぎても困る.それで,複素平面上の 2 点を指定することで積分範囲を定めることにしてみよう.始点から終点まで複素平面上を駆けまわるようなコースをたどりながら短冊の面積を足して行くことにするのだ.

短冊の面積についてはどう考えたら良いだろうか.今や積分しようとしている関数 f(z) も複素数の範囲で値を持つのであり,「面積」を計算するという解釈にこだわることに意味は無い.面積を意味しなくていいのなら,「短冊の幅」に相当していた微小区間についても複素数の範囲で考えるようにすればいいだろう.コースに沿って微小な移動を繰り返しながら積分を実行してゆくわけだが,その移動幅は複素数で表されているではないか.その値と,その地点での関数の値を掛け合わせた複素数値を「短冊の面積」の代わりとするのである.

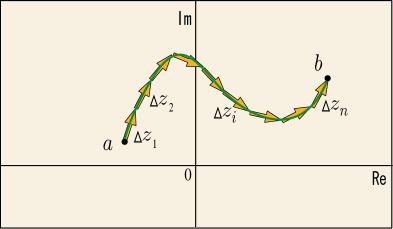
この計算の考え方を式で表せば次のようになる. しかしこれには大きな問題がある.複素平面上の 2 点を結ぶコースは色んなものが考えられ,積分の値はコースに依存することになるのだ.コースが変われば積分の値も変わる.積分の値を決めるには,コースも指定してやらないといけない.そこが実軸上だけの積分との大きな違いである.

この積分のコースのことを「積分路」または「積分経路」と呼んだりする.意味が通じさえすれば「道筋」と呼ぼうが「軌道」と呼ぼうが「コース」と呼ぼうが,「道」,「進路」,何でも構わないのだけれども.

計算法

これで複素積分の定義と考え方は説明し終えた.次に,その具体的な計算の方法を説明しておかなくてはならないだろう.

まず,積分路の形が数式を使ってキッチリ表されている必要がある.これから計算しようというのだから,曖昧なことがあってはならない.それは z(t) という複素関数として表されているとしよう.

変数を時刻に例えると分かりやすいかも知れない.時刻 t=0 には複素平面上の z(0) という位置におり,時刻 t=1 には z(1) という位置にいるとする. z(0) が始点で z(1) が終点を表している.途中の時刻には複素平面上の z(t) という位置を移動中なのだと考えればいい.

移動中のごく短い時間間隔の間に複素平面上をどれだけ進むかと言えば,この z(t) を微分してやったものにを掛ければいいのである.速度と距離の関係に似ているよな？今はを時刻にたとえているだけであって本当に時刻を意味しているわけではないし, z(t) の値も複素数なのだから距離を意味しているわけでもないのだけれども.は積分路を表すためのただのパラメータだ.

これを使えば,複素積分は次のように変形できるであろう. 結局,実数を 0 から 1 まで積分することになるので積分範囲は [0,1] である.ここでは被積分関数が f(z(t)) dz/dt という形になっており,複雑に見えるかも知れない.しかし具体的な計算をする際には f(z) の変数であるの部分に積分路 z(t) を代入してやればいいわけだし,全体としては変数だけの何らかの関数になるだろう.それは複素数の範囲で値を返すような関数だから u(t)+iv(t) という形に書けるに違いない.この考え方を入れて先ほどの続きを書いてみよう. このように,ただの実数の積分を計算すれば良いだけになった少し面倒に見えてしまったかもしれないが,こんなものは「百聞は一見に如かず」だ.具体例を一つやって見せよう.大したことはないということが分かるはずだ.

具体例（その 1）

経路

を点

から

へ向かう直線だとする.
この経路に沿って関数 f(z)=2z

を積分せよ.

始点が,終点がだとすると, z(t)=(b-a)t+a としてを 0～1 の範囲で動かせばからへの一直線の道を表すことが出来る.今回の場合は次のように表せばいいだろう. これ以外の表し方もできなくもないが,今回は素直にこれで行こう. とまぁ,こんな具合だ.面倒なのは確かだが,理解が難しいというところはないだろう.

これでは単純すぎるので何か掴み損ねてはいないかが心配だ.代わりに f(z)=2z^2 を積分してみたらどうなるかを見てみよう. う～ん,すまない.思った以上に面倒くさそうなのでここまでやって気力が失せた.続きはやらなくても大体どんなことをすればいいか分かるだろう.

例題作りの反省点

今の例では積分路を直線的に選んだので簡単すぎて少し面白くない.例えば次のようなコースを例題にしておけばクネクネしたコースになって面白かったのではないか？こうすれば z(t) を微分したものにもが残るので,そういうこともあるのだと読者に印象付けることができたかも知れない.

パラメータ変数を 0～1 の範囲で動かしているが,これも別に深い意味があるわけではない.単純な数値を使えば計算が簡単になるだろうという配慮であった. -2≦t≦3 の範囲で動かすなんて例を用意しても良かったかもしれないが,最初にやる具体例としては複雑すぎるか・・・.

そう言えば,直線コースであっても微分にを残すことはできそうだな.先ほどの具体例のを t^2 とか t^3 とかに置き変えてやればいい.直線上をの増加に合わせて一定速度で移動するのではなく,加速しながら移動するようなイメージだ. これを使っても計算の結果は先ほどと変わらないのである.コースの形が結果に影響するのであって,コース上を移動する速度のようなものは影響を与えない.興味のある読者は試してみてもいいだろう.

このように,伝えたい微妙なニュアンスは沢山あるのだが,それらをひとつの例題に詰め込むのは難しい.かと言って,わざわざ多数の例題を繰り返す手間を掛けるほどのことでもないだろう.

円形の経路を表す方法

経路を表すのに次のような形式のものもよく使われる. これは原点を中心とした半径の円形のコースだ.ピンと来ない人は前回の話を思い出してもらいたい. $re^{iθ}$ を使って複素平面上の位置を表すことができたのだった.は半径では偏角である.今はの代わりにを使っているだけだ.を動かせば,半径が一定のままで複素平面上を原点を中心にして回ることができるのである.

さて,というのは単なるパラメータとして導入しただけであって,別にどんな記号を使ってもいい.もちろんを使ってもいい. むしろこうした方が図形的なイメージが湧きやすいであろう.パラメータを動かす範囲は 0～1 とは限らないのだから,始点を θ=π/2 として終点を θ=π としても構わないのである.こうした場合,それは虚数軸上のから左に向かって 90°の弧を描いてへと至る道筋を表すことになるだろう.

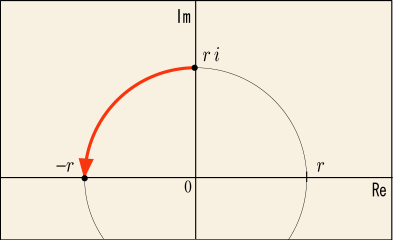
こんな具合に,実数のパラメータを一つ用意して好きなように積分路を決めてやればいいのである.

具体例（その 2）

では今話したことについても何か実例をやってみよう.

経路

を $z(θ)=3e^{iθ}+2i , (0≦θ≦π)$ とする.
この経路に沿って関数 f(z)=z^2

を積分せよ.

この z(t) は複素平面上の点を中心にして半径 3 の半円を描くような道筋を意味している. この変形過程で,実数の不定積分と同じ公式が成り立つかのように計算してしまっている.指数関数が虚数を含んでいるにもかかわらずだ.そんなことをして問題がないなどとは,ここまで一言も言っていない！実数の積分と同じ計算法を使おうとすると問題が起こる場合があるので気を付けないといけないのだ！

本来は次のようにすべきである.前回やった $e^{iθ} =cosθ + isinθ$ という公式を使って実部と虚部に分け,それぞれを実数の積分に直して計算するのである.ところがその結果は再び指数関数の形に書き戻すことができて,結局は指数関数の不定積分と似たルールが成り立っていることがわかる.本当にそうなっているのか試してみよう. なるほど,確かに成り立っているようだ.先ほどはわざわざこういう手順でやるのが面倒だったので途中をサボっただけである.

実数の不定積分と同じルールを使うべきでないと言われると,能力を制限されたようで窮屈さを感じることであろう.使って良い場合と,使うと失敗する場合があるのだ.それについてどう判断すべきかは次回以降の話で明らかにして行こう.

具体例（その 3）

今の例は少し簡単過ぎた.ここまでの具体例を見ただけの読者が,自信を持ってあらゆる問題に対処できるようになるだろうか？もう少し厳しい例を見せておいた方がいい気がする.

経路

を $z(θ)=3e^{iθ}+2i , (0≦θ≦π)$ とする.
この経路に沿って関数 f(z)=1/z

を積分せよ.

経路は先ほどと同じにしておいた.関数を f(z)=1/z に変えたのである. ここで一旦立ち止まる.こんな形の積分はたとえ虚数が含まれていなかったとしても難しいものだが,先ほど実数の不定積分のルールも安易に使ってはいけないと言われたところなので,もうどうやって進めて行けば良いものやら困ってしまう.

しかしあまり道具に頼ることを考えないで,基本に忠実になってみよう.実部と虚部に分けることを試みるのである.オイラーの公式を当てはめよう. これが実際に解けるかどうかはさておき,この最後の積分はどちらも虚数を含まない形になっているのだから,実数の積分のルールを使って解くことに対して文句は出ないであろう.

さて,計算の途中ではあるが,言いたいことは言い終えたのでここまでにしておこう.答を出すこと自体は重要ではない.

積分路に関する性質

積分路は一つの式で表せるようなものでなくても構わない.だいたい,複雑な進路をたった一つの式で表そうだなんて無茶というものだ.

積分路を二つ以上に分けてそれぞれを計算し,後からそれらの和を取っても構わない.同じことだが,次のように言ってもいい.一つの積分の終点と次の積分の始点がちゃんと繋がっていれば,それを一つの進路だとみなすことができる,と.この性質を式で表せば次のように書けるだろう. ここで $C_{1}+C_{2}$ と書いた積分路は,積分路 $C_{1}$ と $C_{2}$ とが繋がって出来ている一つの積分路を意味している.一例を図に表してみよう.

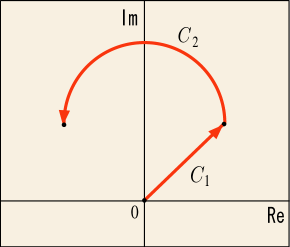
この図にあるように,積分路の繋ぎ目には角があっても構わない.計算するためには積分路を微分する必要があるので経路は滑らかである必要があるが,せいぜい有限個の角があるくらいの経路なら分けて計算すればいいのだから問題はないのである.

もう一つ,積分路について重要な性質がある.積分路を逆にたどって計算すると,符号が逆転したものになる. ここで左辺の積分路をと書いているが,これは積分路を逆にたどって進むという意味で良く使われる書き方である.

他の基本的な性質

あまり説明しなくても分かると思うが,ついでに次のような性質があることも書いておこう. これは積分路が同じ場合,和の形になった被積分関数を別々の項に分けて積分しても値は変わらないということだ.そしてもう一つ. これは積分路が同じ場合,被積分関数を定数倍（複素数でも良い）したものの積分は,後から全体に定数を掛けるようにしても値は変わらないということを意味している.

先ほどの具体例でもすでに使っている性質だ.とりあえずはこれくらい知っていれば良いのではなかろうか.

ひとまず説明完了

複素積分の基本は説明し終えた.

しかしこれであらゆる問題に対処できるようになったかというと,もちろんそういうわけではない.実数の積分と同じように,複雑な関数を積分しようとすればやはり困難があるだろう.小手先のテクニックやひらめきによる式変形が必要になることもある.そういうものについてはいちいち説明する予定はない.

例えば,f(z) = z²z^* という関数を「原点を中心にした半径 r の円軌道」で積分する際には zz^* = |z|² = r² だと言えるから f(z) = r² z という関数だと考えて計算した方がよっぽど簡単になるだとか,そういうことに気付くのと気付かないのとでは大きな差が出ることだろう.

では次回から説明しようとしているのは一体どういった内容なのだろう？

実は複素積分にはとても面白い性質が隠されているのである.それを知れば,今回説明したようなややこしい計算をほとんどすることなく,問題を見ただけで答を言い当てることすら出来る「ことも」ある.その為には特別な条件を満たしていないといけないので,そういう技がいつでも使えるというわけではないのだが,知れば視野が広がることは間違いない.

今回の具体例も,本当はもっとずっと簡単に計算できるのである.いや,待てよ・・・最後の例だけはこれ以上簡単にはならないかも知れないな.