典型的な例
今回は一次変換の幾何学的な意味を考えてみよう.分かりやすいように図を使って考えるという意味だ.立体的な図を描くのは面倒だし読者にも解読の負担が掛かるので,しばらくは 2 次元に制限して考えることにしよう.
一次変換というのは単純で不自由な変換である.それは仕方ない.行列に載せることのできる情報なんて限られているからだ.典型的な例を示してみよう.
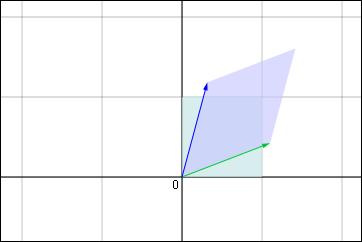
これはかつ
の正方形の領域内に含まれる無数の点をそれぞれに一次変換した結果を集めてみると,全体としてどんな領域に移動するのかを示したものである.正方形の領域から菱形の領域に移動しているのが分かる.この菱形の領域のどこかに,変換後の点が特に集中しやすい場所があるということはない.それが分かりやすいように市松模様を付けて描くと次のような具合である.
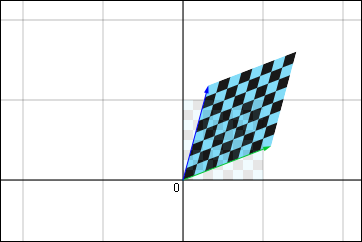
これでおおよその状況が分かって貰えただろうか.こんな具合に平面の全体が,一様に似たような変換を受けて移動するのである.
線形性
平面全体が一様に似たような変換・・・?これでは表現が曖昧すぎる.せめてもう少し,状況を正しく伝えるマシな言い方はないものだろうか.「原点からの距離が 2 倍遠くにある点は,変換後も 2 倍遠くへ移される」とかではどうだろう・・・.確かにそうなっている.
この変換の特徴を美しくまとめてみたい.どうしたらいいだろうか.まずは点の位置をベクトルで表そう.点と点
を行列
で一次変換してやると,それぞれ
と
へと移動するとしよう.式で表すと次のような具合である.
これを前提にして話してみよう.先ほど書いた性質,すなわち,あらかじめ 2 倍しておけば 2 倍遠くに飛ばされるというような性質は,次のように定数
を使って表せばより一般的な表現になる.
倍した
は,
倍した
へと変換されるのである.
気付きにくいかも知れないが,この他にこんな性質もある.
あらかじめ二つの位置ベクトルを足したものを変換した結果は,それぞれを変換した結果を足し合わせても同じであるというものだ.
これら二つの性質のことを「線形性」と呼ぶ.敢えて言葉にすれば「ベクトルの和や定数倍の操作を,変換前にやっても変換後にやっても結果は同じ」というイメージである.
二つの性質を一度に表したければ,定数の他に定数
も導入して次のように書けばいいだろう.
1 次変換でこの性質が成り立っていることを式を使って確かめるのは本当に簡単だから,各個人で確認してもらいたい.試しに 2 次式を使って変換した場合について調べてみれば,これが成り立っていないこともすぐに分かるだろう.この性質は一次変換(線形変換)だからこそ成り立っていると言える.それだから「線形性」と呼ぶのである.
行列の中身と変換のイメージ
次にこのような変換の情報が行列の上にどのように載せられているかを見てみよう.その為にはというベクトルと
というベクトルがそれぞれ変換される様子を確かめれば分かる.変換行列を
とすると,
の行き先
は
であり,
の行き先
は
である.つまり,それぞれの行き先のベクトルが行列の中に「列」として表されているわけだ.「二つの座標軸に接する一辺の長さが 1 の正方形」(うす緑の領域)は,「これら二つのベクトルを二辺とする平行四辺形」(うす紫の領域)に移動させられるのだと考えればいい.
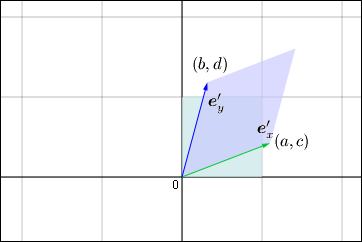
すると,一次変換の様子は,この二つのベクトルと
がどこに変換されるかによって決まってしまうことになる.
上に描いた典型例ではと
とが,互いに近付く方向に変換されていた.しかし次の図のように互いに離れる方向に移動することだってある.
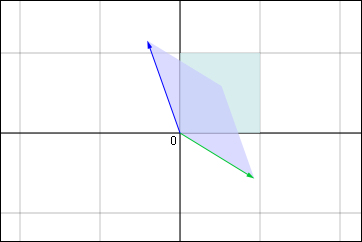
あるいは,どちらも同じ方に向かって回転するかのように移動する場合だってあるわけだ.
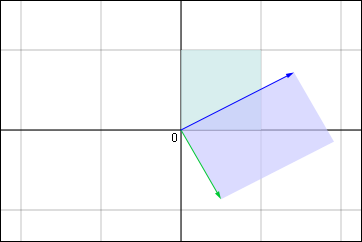
もしと
が両方とも元の位置から同じ角度だけ移動して,しかも長さが変化しなければ,それは平面全体を回転させるような変換だと言えるだろう.例えば角度
だけ回転させる行列は次のように表される.
他にも
軸と
軸とを逆転させてしまうような変換も考えられる.もし元の領域に絵が描いてあったとしたら,この変換ではまるで絵の裏表が逆になったように変換されるだろう.
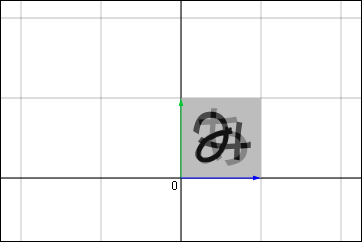
これは軸の向きを逆転させてから -90°の回転をさせたのと同じことである.
絵を裏返すか,回転させるか,菱形にするか,線形変換で出来ることはだいたいそれらの組み合わせだと言えるのではないだろうか.
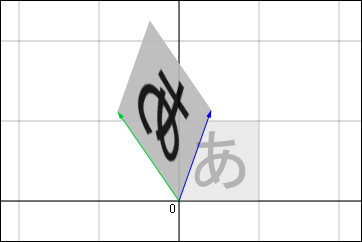
最後に,これまでで最も特殊な例を挙げておこう.
二つのベクトルと
が全く同じ方向,あるいは互いに全くの正反対の方向を向いていた場合には,平行四辺形はつぶれてしまい,ただの直線になってしまうだろう.つまり,平面上のあらゆる点は変換されて,そのたった一つの直線の上に乗ってしまうことになるのである.
実はこれが,逆行列が存在しない場合のイメージである.平面全体が直線になるまで潰れてしまったら,もう戻しようがないのである.この時の行列式は 0 になる.おっと,これは前回も話したっけ.大事なことなので二度言いましたよ,ってことで.
試してみよう
以上で説明したことを読者自身が操作して実感してもらえるように,ウェブアプリを作ってみた.
使い方の説明の中で「基底ベクトル」という,まだ説明していない用語が出てくるが,感覚で理解して軽く受け流してもらいたい.それ以外の簡潔な表現が思い付かなかったのである.その用語についてはあとでもう少し正しく説明するつもりである.
行列式の意味
平行四辺形が完全に潰れてしまう時に行列の行列式が 0 になる理由はここまでに話した事柄を使って簡単に説明できる.平行四辺形が潰れてしまうような行列の中には平行な二つのベクトルが列の形で書き込まれているであろう.つまり,一方の列は他方の列を定数倍した形になっているはずだ.ところで,「同じ内容の列が二つ存在していると,その行列式は 0 になる」のであった.また,「どこかの列を定数倍すると,その行列式も同じだけ定数倍される」のだった.0 を定数倍しても 0 だから今考えている行列の行列式もやはり 0 だというわけだ.
しかしそれ以上の事実がある.行列式というのは実は二つのベクトルが作る平行四辺形の面積を表しているのである.2 次の行列の行列式はであるから図を使って本当にそうなっているか確かめてみれば良い.中学生でもできそうなことなのでわざわざここでやる必要はないだろう.
ここまで 2 次元の話しかしてこなかったが,3 次元以上でも同じようなことが言えている.しかし 3 次元の場合には面積ではなくて体積である.3 次元の 3 つの基本ベクトル,
,
というのは,一辺の長さが 1 の立方体の 3 つの辺になっている.
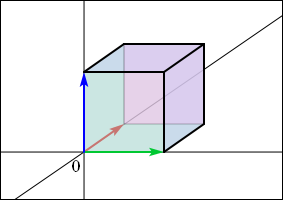
これらのベクトルが 3 次の行列で変換されると,この立方体はひしゃげて,平行四辺形の立体版である「平行六面体」というものを形作る.
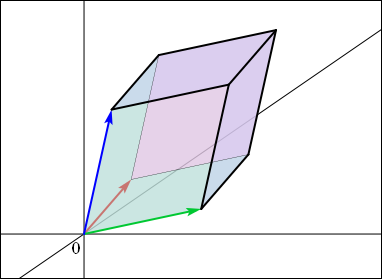
3 次の行列の行列式はこの平行六面体の体積を表しているのである.これを幾何学的な方法で確かめるのは少し骨が折れるに違いない.
しかしこれらの事実を苦労して確認してみたとしても,それだけではどうにもすっきりしない.一体なぜそんなことになっているのだろうか?行列式の定義が,たまたまではなく,面積あるいは体積と一致していると言える根拠はどこにあるのか.この説明は後からしよう.
とにかくこういうことが成り立っているのであれば,逆行列の行列式がもとの行列の行列式の逆数になっていることも自然に理解できる.変換すれば面積は倍,元に戻せば
倍だ.また,行列の積の行列式を求めるときに,単純にそれぞれの行列式の積を計算すれば良かった理由についても容易にイメージできる.これは複数の行列を使って立て続けに変換されるときに,一番最初と一番最後の状態を比較してみると,結局のところ領域の面積が何倍に拡大,縮小されたことになるのかという意味を素直に表していたというわけだ.
ところで行列式が負値になることもある.面積が負になるというのはおかしな話だが,それは先ほどの例で言えば,絵が裏返しになる場合を表しているのである.
行列式が面積や体積を表す理由(2 次元の場合)
行列式が,変換前後での領域の面積変化や体積変化を表していることを簡単に確認する方法があるので紹介しておこう.まずは慣らしのために 2 次元で説明する.
二つの 2 次元ベクトルと
によって作られる平行四辺形の面積を
と表すことにしよう.
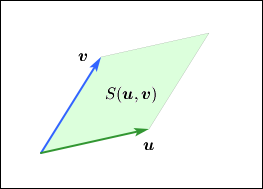
このには次の性質がある.まず一つ目.
でも
でも,どちらか片方のベクトルを
倍したものは元の
倍になる.
図で表しておこう.一目で納得できるだろう.
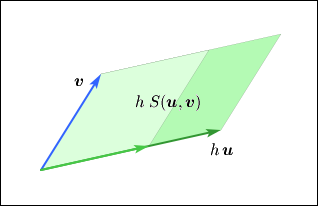
ここではの方を
倍してみたが,
の方についても同じである.念のため式を書いておこう.
他にも重要な性質がある.一方のベクトルに全く別のベクトル
を加えたときには次のように展開して表すことができる.
これも図で表しておこう.
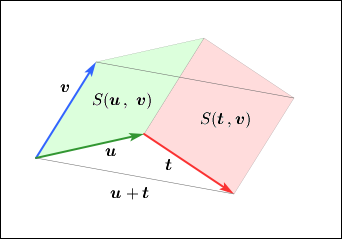
ここではの方に
を加えてみたが,
の方に加えても同じである.この式も念の為に書いておこう.
(1) 式と (3) 式を次のようにして一つの式に表すことができる.
この形は今回の最初の方で説明した「線形性」に良く似ているだろう.(2) 式と (4) 式についても一つにまとめることが出来て,やはり (5) 式と同じような性質が成り立っていることが言える.
線形性に似た性質が
の各成分について同時並行で成り立っているこのような性質を「多重線形性」と呼ぶ.
すでにの性質について沢山の事を説明したように思うかも知れないが,実はまだ多重線形性しか説明していない.ずいぶん多くの言葉を費やしたものだ・・・.
もう一つ,には分かりやすい性質がある.もし
と
とが同じベクトルなら,平行四辺形はつぶれてしまって,面積は 0 になる.
この性質には特に名前は付いていないが,ここから面白い性質が導ける.そのために,これから
という量を計算してみよう.計算しなくても (7) の性質から,この値が 0 になることはすぐに分かる.しかし敢えて,先ほど説明した「多重線形性」を使って変形してやるのである.今後の計算練習を兼ねてやってみよう.次のようになる.
このような計算をしなくても,この全体が 0 になることはさっき話した.結局は次の式が成り立っているということだ.
書き換えればこうだ.
つまり,
と
とを入れ替えると
の符号は反転するのである.
は面積を表すと言ったわけだが,今考えている
というのは負の値を取ることも許されている量だと認めて欲しい.この (8) 式の性質を「交代性」と呼ぶ.
(7) 式から (8) 式を導くような説明法を選んだが,「多重線形性 + (7) 式」と「多重線形性 + (8) 式」は同値である.結局ここまでで「多重線形性」と「交代性」を丁寧に説明してきただけである.
最後にもう一つ,面積の大きさを規定しておこう.基本ベクトルと
を代入したときの値を次のように決めておく.
これで準備完了だ.
ここからが本題である.しかしすぐ終わる.次のような行列について考えてみよう.
この行列の行列式は
である.この行列によって二つの基本ベクトル
と
はそれぞれ,
と
へと変換されるのだった.
ではこれから,これら変換後のベクトルが作る平行四辺形の面積を求めてみよう.ベクトルは
と書けるし,ベクトル
は
と書くことができるだろう.これらを先ほどの
に代入して計算してやればいいのである.ここまでに説明した性質を総動員することになる.
こうして求まったのは平行四辺形の面積であるが,同時に,先ほどの行列の行列式でもあるわけだ.これらがなぜ一致するのか,分かるだろうか.
行列式が面積や体積を表す理由(3 次元の場合)
今の話と同じことを 3 次元の場合でもやってみよう.3 つのベクトルが作る「平行六面体」の体積をと表すことにする.3 次元の場合でも次のような多重線形性が成り立っている.
この式はあんまりじっくり見なくてもいいだろう.だいたい上と同じことを言ってるだけなので.ああ,でも並べると綺麗だなぁ.
3 次元の場合の交代性というのはの中のどれか 2 つのベクトルが等しければ 0 になるということである.あるいは,「三つの内のどの二つのベクトルでも入れ替えれば符号が逆転する」と考えても同じである.すべての場合を書くのは面倒だし,もう式は書かなくても良いだろう.でも考えてみたら 3 通りしかない?まぁいいや.
そして,体積の大きさの規定.と決めておく.
これらの性質を使って 3 次の行列が作る平行六面体の体積を求めてみよう.行列としては次のようなものを考える.
これによって三つの基本ベクトル
,
,
はそれぞれ,
へと移されるから,
というものを計算してみればいい.きっと 3 次の行列の行列式と同じ結果となるだろう.
しかし,ここではその計算はやらない.バイクの運転やスキーの滑り方と同じように,いくら理屈を並べても伝わらない微妙なニュアンスってものがあるからだ.ぜひ読者自身で試してみることでそれを感じ取ってもらいたいのである.
行列式が面積や体積を表す理由(n 次元の場合)
平行六面体の体積を求める作業を実際にやってくれた読者になら,これを次元に拡張して計算した時にどのような手順を踏むことになるのかを想像するのは容易になっているだろう.臆せずに考えてみてもらいたい.
行列式の定義式と全く同じ意味の作業をしていることに気付くはずだ.それは例えば,成分の並びを変えるたびに項の符号が変わるところとか,必要のない項が自然に消えて行って,結局は行列の各行から列を一つづつ重複しないように選んで積を取っているところとか・・・.やってみた人でないと分かりにくい説明であることは分かっている.申し訳ないが,これを図と文章だけで伝えようとするのは本当に手間が掛かる.
目の前にいる相手に同じノートの上で計算しながら説明できればずっと楽なのだが,本当はそうしたいくらいなのだが,それも叶わない.やってみた人には私が何のことを言っているのか,伝わるはずだ.










