物理数学：線形独立とランク

行列式が 0 になるイメージ

行列の行列式が 0 になるのは,例えば 2 次元の場合には「二つの列をベクトルとして見たときに,それらが平行になっている場合」あるいは「それらのベクトルのどちらか一方でも零ベクトルである場合」とまとめてもいいだろう,多分.

ところが 3 次元以上の場合を考えてみるとそれだけでは済まない気がする.例えば 3 次元で考えてみよう.

3 次の正方行列には 3 つの列ベクトルが含まれる.これら全てのベクトルが平行である場合には,これらが作る平行六面体は一本の直線にまで潰れてしまって,3 次元の全ての点が同一直線上に変換されることになる.（下の図ではわざと 3 つのベクトルを少しずらして描いてある.ベクトルを完全に重ねて描いてしまうと何の図か分からないので.）

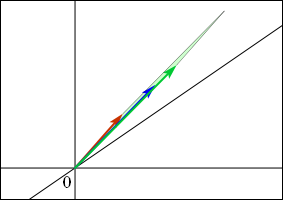
一度こうなるともう元のようには戻せず,行列式は 0 である.ここまでは 2 次元の場合とそれほど変わらない話だ.

ところが,それらの列ベクトルのどの二つを取り出して調べてみても互いに平行ではないような場合でも,それらが作る平行六面体の体積が 0 に潰れてしまっていることがある.それは 3 つの列ベクトルが全て同一の平面上に乗ってしまうような状況である.こういう行列を使った時には 3 次元の全ての点が,平面上の点に変換されてしまうことになり,もう元には戻せない.この場合にも行列式は 0 である.

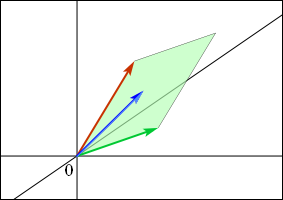
どうやら,ベクトルが平行かどうかという分かりやすい基準だけでは行列式が 0 になるかどうかを判定できないらしい.

このように,行列式が 0 になると言っても,直線上に乗る場合もあれば平面上に乗る場合もあるわけだ.行列式の値だけではこれらの状況の違いを区別できない.これらを的確に分類するにはどういう考え方を取り入れたらいいだろうか.

ランク

線形代数のかなり初めの方で説明した内容を思い出してもらおう.行列を使って連立方程式を解くときに使った「必勝パターン」すなわち「ガウスの消去法」あるいは「掃き出し法」についてだ.「二つのルール」を繰り返して,上三角行列を作るように努力するのだった.その作業の結果,どこかの行がすべて 0 になってしまうという結果に陥ることがあるのだった.それは問題設定のせいであって,手順の不手際によるものではないのだった.

さて,この作業が終わったあとで,一行がまるごと全て 0 になってしまった行がもしあれば除外してみよう.幾つの行が残っているだろうか？その数のことを行列の「ランク」あるいは「階数」と呼ぶ.このランクという言葉は「今週のベストランキング！」みたいに使うあのランクと同じ意味だ.「行列のランクはである」というのを式で表現したいときには,次のように書く. ちゃんと理解できたかどうか確かめるために,当たり前のことを幾つかしゃべっておこう.もし次の行列を変形して行った結果,各行とも成分がすべて 0 になるということがなく,無事に上三角行列を作ることができたならば, である.

次の行列を変形していった結果,一行だけ,成分がすべて 0 になってしまったならば, である.単純な話だろう？

では,このランクとは,一体何を表しているのだろうか？その為に,さらにもう少し思い出してもらおう.先ほど思い出してもらった話からさらに幾つか進んだ回（実はたった二つ前）では,「ガウスの消去法」というのは実は基本変形行列というものを左から掛ける作業と同じことだ,と説明している部分がある.

基本変形行列には幾つかの種類があったが,その内のどのタイプのものであっても,次元空間の点を次元空間へと移動させる行列である点では同じである.つまり次元は変らない.ところが,ある行がそっくり丸ごと 0 になってしまった行列というのは,これを変換に使ったならば次元が下がってしまうだろう.もし次の行列に対して基本変形行列を掛けていった結果,そういう形の行列になってしまったとしたら,つまり,次元空間の点を次元より小さな次元の空間へと移動させる形の行列になってしまったとしたら,ということだが,それでもそれは基本変形行列のせいではないはずだ.ということは,パッと見では分かりにくかっただけで,行列が元々そういう行列だったということを意味する.

要するに,ランクとは,全空間を何次元の空間へと変換することになる行列であるかを表しているのである.このランクという概念を使えば,行列式が 0 になるような行列をさらに細かく分類することが出来るだろう.

数学の教科書にはこれ以外にもランクを使った様々な定理が載っているかも知れないが,とりあえずこれくらいを知っていれば簡単な問題には即答できるだろう.複雑な問題というのは幾らでも作り出せるものだから,あまり気にしてはいけない.もし即答できない問題に対処する必要が出て来れば,その都度調べて知識を増やしていけばいいのだ.

それに,あまりここで言うことでもないのだが・・・,物理の問題を考えるときにはランクの概念をこねくり回してあれこれと議論する機会はほとんどないであろう.

線形独立、線形従属

こうして,線形変換に使う行列とランクとの関係を説明し終えたわけだが,まだ何かやり残した感じがしている.というのも,今回の冒頭では,行列の中に列の形で含まれているベクトルのイメージを重視していたはずだ.しかしここまでのランクの説明ではベクトルのイメージがまるで表に出ていないのである.

そこで別の見方で説明することも試みよう.とりあえず,ベクトルについて,線形変換から少し離れた視点で眺めてみることにする.

複数のベクトルを集めたとき,その中の一つが他のベクトルを組み合わせて表現できるかどうかということについて考えてみよう.組み合わせるというのは,定数倍したり和を取ったりするということである.これを「線形和」と呼ぶ.線形和を使って他のベクトルを表現できる場合には「それらのベクトルの集まりは互いに線形従属である」と表現し,出来ない場合には「それらのベクトルの集まりは互いに線形独立である」と表現する.

注：線形独立,線形従属という言葉の代わりに一次独立,一次従属という表現が使われることもある.

要するに線形従属であるというのは,どれか一つ,あるいは幾つかのベクトルが他のベクトルの組み合わせで代用できるのだから「どれかが無駄に多い」状態なのである.特にどのベクトルが「無駄の張本人」だと指摘できるわけではなくて,互いに似たような奴等が同じグループ内に含まれてしまっている状態である.

冗談：遊び仲間の中でキャラが被ってる奴がいるとき「俺たちって線形従属だな」と表現したりする.

言葉を尽くしても正確さに欠ける.この辺りを数式を使って表現してみよう.複数のベクトル $a_{1},a_{2},…,a_{n}$ があるときに,係数 $c_{1},c_{2},…,c_{n}$ を使って次のような式を作る. この左辺のような形が先ほど話した「線形和」の典型例だ.係数 c_k のいずれもが 0 ならばこの式はいつだって当然の如く成り立ってしまうので面白くない.しかしそうする以外にこの式を成り立たせる方法がないとき,この式に使われたベクトルの組 $a_{1},a_{2},…,a_{n}$ は線形独立だと言えることになる.それはなぜかって？もし線形従属なら,他のベクトルの影響を打ち消して右辺を 0 にする方法が他にも見つかるはずだからである.

誤解をなくすためにもう少し説明しておこう.例えばこの (1) 式を変形してのようにしてみよう.これはベクトル $a_{1}$ を他のベクトルの組み合わせで表現できるという意味になっている.線形従属のイメージそのものだ.ただし,どの c_k も 0 だという状況でない限りは,という条件付きの話だが.全ての c_k が 0 だったなら線形独立である.

いや,(2) 式にはまだ気になる点が残っているなぁ. $c_{1}=0$ である場合には式が破綻しているのではないか？それは $a_{1}$ を他のベクトルの組み合わせで代用することが無理だったという意味だ.(1) 式に戻って考えるといい. $a_{1}$ の効果を打ち消す手段が他にないから $c_{1}=0$ と設定することで打ち消さざるを得なかったということだ.

このように,他のベクトルで表せないベクトルが混じっている場合,その係数は 0 としておいても構わない.それでも全ての係数 c_k が 0 だという状況でない限りは線形従属と呼ぶのである.だから幾つかの係数が 0 になっていてもいいわけだ.もう一度まとめて言い直そう.他のベクトルによって代用できない「独立した」ベクトルが幾つか含まれている状況であったとしても,「このベクトルの集団は線形従属である」と表現することに躊躇する必要はない.それはごく普通に起こり得ることである.

線形独立の判定

線形独立か線形従属かを判別するための決まりきった手続きがあるとありがたい.複数のベクトルを用意した上で,それらが (1) 式を満たすような個の係数 c_k の値を探す方法を考えてみる.次のような 3 次元のベクトルを例にして考えてみよう. これで (1) 式と同じものを作るとであり,次のようにも書ける. これは連立一次方程式なのではないかという気がしてくる.少し書き直せば,こういう連立方程式と同じ形ではないか. 未知数は $c_{1}$ , $c_{2}$ , $c_{3}$ の 3 つ.これを解くには係数部分だけを取り出して行列を作ればいいのだった. あっ！3 つのベクトルを列ベクトルの形で並べて行列に入れる形になっている！これは一次変換に使った行列と同じ構造ではないか.しかし今は連立方程式を解くための行列でもある.何だか同じような話に何度も戻ってくるような感じだが,今は無視して計算を続けよう.

さあ,思い出せ！連立方程式がただ一つの解を持つ条件は何だったか？それは行列式が 0 でないことだった.

今の場合,ただ一つの解というのは明白で,未知数 $c_{1}$ , $c_{2}$ , $c_{3}$ がどれも 0 だというものだ.行列式が 0 でなければ,解はそうなるはずだ.その時 3 つのベクトルは線形独立だということになる.一方,行列式が 0 であったならば解は一通りには定まらず,すなわち「全ての係数が 0 になる」という以外の解があるわけだから,3 つのベクトルは線形従属だということになろう.

行列式が 0	→	線形従属
行列式が 0 以外	→	線形独立

ということだ.

今の計算過程で,線形変換を思い出させる形が顔を出してきていた.実は論理的には同じことをやっているだけということだろうか？だとすればイメージを統合できるかもしれない.

線形変換のイメージを思い出すと,行列の中に縦に表されている複数のベクトルによって,平行四辺形や平行六面体のような形の領域が作られるのだった.その面積,あるいは体積は,行列式と関係しているのだった.一方,今の計算から分かったように,行列式はそれらのベクトルが線形従属か線形独立かということとも関係しているのだった.

ということは,それらのベクトルが線形従属か線形独立かによって,それらが作る領域の面積,あるいは体積が 0 に潰れたり,潰れなかったりすると言えるわけだ.ランクというのはその領域の次元を表しているのだった.ランクを調べれば,これらのベクトルの集まりが結局何次元の空間を表現できるのかが分かるということである.

線形従属である場合には,そこに含まれるベクトルの数よりも小さな次元の空間しか表現することができない.幾つかのベクトルは,それ以外のベクトルが作る空間の中に納まってしまって,新たな次元を生み出すのに寄与していないのである.

線形従属であるようなベクトルの集まりから幾つかのベクトルをうまく選んで捨てることで,線形独立なベクトルの集まりにすることが出来る.余分だったものを捨てるわけだ.この時,線形独立なベクトルを最大で幾つ残すことができるかを表しているのがランクであるとも言えるわけだ.

列の方をベクトルとして考えないといけないのか？

ここまでは「行列の中に含まれる各列をベクトルの成分だとみなした場合に」などという表現が繰り返されているが,列ではなく行の方をベクトルの成分だとみなして考えてはいけないのだろうか？

例えば次のような連立方程式を考える. これらの式がそれぞれに独立な意味を持っているかどうか,ということが気になることがあると思う.独立でなければ解が一通りに定まらなかったり「解なし」ということになったりするだろう.

しかしそういう事を考えているとき,これらの式から係数を抜き出して作った次のような行列の列の方ではなく,各行の成分の方を「ベクトルに似た何か」として見ているようなものである. そういう考え方をしても問題はないだろうか？

結論としては問題ない.列を取り出してベクトルとして考えてきたのは幾何学的な変換のイメージから話を進めた都合である.行列式の計算については「行で成り立つことは列についてもそのまま成り立っている」のだった.だから列と行を入れ替えたとしても最終的な値は変らない.またランクを求める過程についても,列への操作と行への操作は,基本変形行列を右から掛けるか左から掛けるかの違いだけなので,どちらにしても答えは変らない.

このことを式で表わしておこうか.式を使って証明しようというわけではない.今話したことをまとめ直すだけである.数式で表現されているだけで安心して受け入れられるという人は割りと多いからね.

先ほどの行列の中の各行を列にして書き直すと次のようになる. これを ^t M と書いたのは,行列の転置行列という意味である.すでに余因子行列のところで軽く説明したことがあるが,もう一度説明しておこう.「転置行列」というのは行列の中の (i,j) 成分を (j,i) の位置に置き換えたものだ.正方行列の左上から右下に線を引いて,その線を対称線として中身を入れ替えた形になる.今回のように行と列の役割を入れ替えたものだと考えてもいい.ちなみに,行列の転置行列 ^t A をさらに転置したもの ^t(^t A) は元の行列と同じものである.ま,元に戻るだけなので当然のことだな. 転置行列の性質について語るついでにこれも書いておこう. との積を計算したものを転置したものは,とをそれぞれ転置して積を取ったものと等しくなる！？そりゃ分かりやすくてありがたい性質だ.しかし積の順序も変えないと成り立たないので注意が必要だ.どうしてこうなるのかは読者が自分で簡単に確かめられる範囲だろう.

さて,先ほど書いた理由により,行列式については次の性質が成り立っている. ランクについても次の性質が成り立っている. 細かいところまで説明してはいないが,ヒントはすでに十分あると思う.もし疑いが生じたなら,自分で具体例を作るなどして確かめてみたらいいだろう.さほど難しくはないはずだ.