物理数学：ナブラの応用

ナブラだけを分離する

前回,関数 U(x,y,z) の傾きを表すベクトルとしてというものを定義した.この $\nablaU$ のことを関数の「勾配」または「グラーディエント」と呼ぶのであった.また,ここで使っている $\nabla$ という記号は単独では「ナブラ」と呼ぶのであった.

さて,このナブラだけをグラーディエントから切り離して,次のようなものであると定義してみよう. ここに出てくる ∂/∂x などは本当はこれだけでは意味がないのだが,「この後ろに来るものに対して偏微分を行う」という意味の記号として受け入れることにしよう.このように,他のものに対して計算の指示を与える記号を「演算子」と呼ぶ.このようなものを導入することで数式の表現に幅が広がるのである.

普段あまり意識していないが「＋」「－」「×」「÷」などの記号も広い意味での演算子である.だから ∂/∂x などを他の演算子と区別する必要があるときには「微分演算子」と呼ぶ.ナブラもまた微分演算子であるが,区別する必要があれば「ベクトル微分演算子」とでも呼んでおけばいいだろう.

演算子を働かせて対象を操作することを「（演算子を）作用させる」と表現する.英語では operate という動詞を使うので「オペレートする」ということもある.数学では演算子 (operator) のことを「作用素」と呼んでいるので数学寄りの教科書を読むときに困惑しないようにしよう.この辺り,物理では翻訳に一貫性がないな.

ベクトルの湧き出し

さて,ナブラだけを分離すると何が出来るというのか？例えば, $\nabla$ とベクトル A=(A_x,A_y,A_z) との内積を作ってみると次のようになる. $\nabla$ ととの内積を作ること自体には理由などない.ただ内積の計算ルールに倣ってこのように定義してみましょう,というだけのことだ.ところがなんと,この右辺の計算内容には意味が見い出せるのである.それをこれから説明していこう.

(1) 式の右辺ではベクトルの位置による変化具合を計算しているらしいことは分かるだろう.このというのは場所によって値が決まるようなベクトルである.空間に無数のベクトルが張り付いて存在しているようなイメージでとらえても良い.前回の話の最後に説明したが,そういうものをベクトル場と呼ぶのだった.

ベクトルが空間を埋め尽くしている様子を想像してみて欲しい.そのベクトルは微分できるように滑らかに変化しているから,どこかを境にして矢印の方向や大きさが突如として不連続に変わるということはない.だから,それはまるで水の流れを表しているようにも感じられる.ある部分ではベクトルが小さくなっていたり,別の部分では大きくなっていたりすることだろう.それに対して,あたかも空間からベクトルが湧き出してきていたり,空間にベクトルが徐々に吸い込まれて消えてしまっているような空想を当てはめてみる.(1) 式の右辺は,そのような空間の各点におけるベクトルの湧き出しや吸い込みの度合いをプラスマイナスの値として算出していることに相当するのである.

なぜそう言えるのだろうか？(1) 式の右辺の第 1 項を見てみよう.これが正の値だとすると,軸の正の方向に目をやるにつれて A_x が増加していることになる.ベクトルを水の流れのようなイメージでとらえると,軸の正の方向に流れる水の流れがどんどん増しているようなものであり,どこか途中に湧き水があるに違いないというイメージになる.

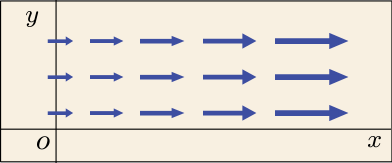
もし第 1 項が負になっていたとしても,代わりに第 2 項や第 3 項が正の値で全体として 0 だったならば,もともと方向に向かっていた水の流れが方向や方向に向きを変えただけで全体としては湧き水があったわけではないのだな,などと解釈できる.

イメージを正しく理解してもらうためにはもう少し色々と説明が必要な気もするが,ここでは式の定義と計算法を分かってもらうのが第一目標なので,軽めの説明で済ませることにしよう.まだ説明が足りないことと言えば・・・,例えば次の図のような場合も第 1 項は正なのである.

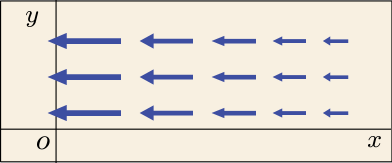
右に目をやるにつれてベクトルは小さくなっているが,これらのベクトルの成分がもともと負だったものが増加していっているために,絶対値が減少しているように見えるだけである.しかしイメージとしては左へ向かって流れる水流が増加しているようであり,途中に湧き出しがあるというイメージは変わらず成り立っていることになる.

このように,水流が右へ流れるか,左へ流れるか,それ以外のどちらへ流れているかに関係なく, $\nabla・A$ が正ならばその地点では水の湧き出しがあり,水量が増加していることを意味しているのである.

もう少しだけ数量的な説明を知りたければずっと前に書いた記事があるのでそちらも参考にしてもらいたい.そこでは電磁気学で使う「ガウスの定理」というものの説明が主題になっていて,まだ説明していないベクトルの積分がいきなり出てくるのだが,そこは軽く読み飛ばしてもらったらいいと思う.ベクトルの積分はもう少し後で説明する予定なので,そこまで理解してから読んでもらっても良いだろう.その記事中では ∇・E を div E と表現しているが,それは今回の記事をもう少し先まで読むと分かる.

というわけで,この $\nabla・A$ のことを,ベクトルの「湧き出し」または「ダイバージェンス」と呼ぶ. $\nabla・A$ は,空間中の場所ごとで一つの数値が決まるものであり,そういうものを「スカラー場」と呼ぶのであった.

ベクトルの回転

ナブラを分離した効用は他にもある.次は $\nabla$ とベクトル A=(A_x,A_y,A_z) との外積を作ってみる.外積の定義に倣って定義してやると次のようなものが出来上がる. 何と,この右辺の計算内容にも意味が見い出せる.ベクトル場を視覚化してみると,渦を巻いているように見える場所もあることだろう.はっきりとした渦には見えなくとも,もしそこに水車を置いたならば,ベクトルの流れの微妙な差によって回転を始めるのではないかと思える場所が幾つもある.

この (2) 式の右辺はベクトルになっていて 3 つの成分を持つが,例えばその第 1 成分は,回転軸を軸方向に向けて設置された水車を空間中に置いた時にどれくらいの勢いで回転するかを表しているのである.この値が正ならば,軸の正の向きを向いた時に時計回りに見えるような回転をしているし,負ならば反時計回りをしていることを意味している.他の軸についても同様である.

この (2) 式の右辺のベクトル全体としては,「もし自由に軸の方向を変えられる水車（それは自由に回転できる羽根付きボールのようなものだろうか）があるとすれば,それはどの方向を軸として右回りするか」というのを表していることになる.しかしそのことを示すのはまだ少しレベルが高いのでやめておこう.

念の為に書いておくと,それは,ベクトル場をそのままに座標軸だけを回転したときに,新しい座標で表した ∇×A の方向がそれに応じてどのように回転するかを確かめれば良い.例えば,∇×A が初めにある方向を向いているとして,その方向が新しい x 軸になるような座標変換をしてやる.もしその新しい座標系で計算される新しい ∇×A が新しい x 軸を向いていれば,新しい y 軸や z 軸の周りには渦成分はなくて,ただ x 軸の周りにだけ渦巻いているということになるからだ.つまり,元々の座標においても ∇×A が示す軸の周りにだけ渦成分があったことになる.

というわけで,この $\nabla×A$ のことを,ベクトルの「回転」または「ローテーション」と呼ぶ.

なぜそんなことが言えるのかを少しだけ説明しておこう.(2) 式の右辺の第 3 成分が分かりやすい.これは水車の回転軸が方向を向くように設置されている場合を示しており,平面内に生じている回転を意味しているのでイメージしやすいだろう.第 1 項は ∂A_y/∂x である.これが正だとすると,方向へ進むほどに流れの成分が強いことになるので,水車の右側の方が強く方向に押され,平面を上から見降ろしていると水車は反時計回りに回転を始めることになる.しかし軸というのは平面からこちらに向かって伸びているものなので,その方向を向いて眺めれば,水車の回転は時計回りである.

第 2 項にどうしてマイナスがついているのかは,同様にして考えれば分かるだろう. ∂A_x/∂y が正の場合,方向へ行くほど方向への流れが強いので,水車は上から見降ろして時計回りすることになるからである.これは先ほどとは逆であるからマイナスが付いていることで話が合うのである.

これについてももう少しだけ数量的な説明を電磁気学の一部として書いたことがある.メインは「ストークスの定理」というものを説明したものなので今すぐ理解できなくてもいいが,参考にはなるだろう.

別の表記法

ここまで $\nabla$ を使って,関数の勾配（グラーディエント）,ベクトルの湧き出し（ダイバージェンス）と回転（ローテーション）を表現してきたわけだが,これらの意味の方を前面に出しての左辺にあるような表記が使われたりもする.このように表した方がナブラばかりが出てくる式よりも分かりやすいかも知れない.この内, rot A は海外ではあまり使われず, curlA が使われることの方が多い. rot だと「腐る」という意味になるからであろう.

私は長い間,これらの記法の方がベクトルの風景をイメージしやすくて好きだったのだが,その内にどちらを使っても同じに思えるようになり,近頃ではナブラを使った記法の方がスマートだと思えるようになってきた.その辺りは慣れや好みの問題である.

ラプラシアン

以上で基本は出揃ったわけだが,もう一つ,良く使う概念がある.少しパターンを変えて,ナブラどうしの内積を作ってみよう. もちろんこれだけでは意味が無い.この後ろに何か微分する対象が来なくてはならない.しかしこの右辺はそれだけで「ラプラシアン」あるいは「ラプラス演算子」と呼ばれている.ラプラシアンは $\nabla・\nabla$ と書かれることは滅多になく, $\nabla^2$ や $\triangle$ のように書かれることの方がずっと多い. (3) 式の右辺の形はラプラス方程式の中に出てくる.いや,ほとんどラプラス方程式そのものだと言えるくらいである.ラプラス方程式というのは次のような形をした微分方程式で,物理をやっていればあちこちで見かけることになる. これをラプラシアンを使って表せば次のように非常にシンプルに表せるのである. この方程式を紹介したのは, $\nabla^2$ がラプラシアンと呼ばれている由来を分かってもらうためであり,ここではこれ以上の深入りはしない.この方程式の性質や解き方についてはずっと後で,微分方程式の話の中で説明するつもりである.ラプラシアンはラプラス方程式以外にも,物理現象を記述する色んな方程式の中で出てくることになる.

余談だが,ラプラシアンは,すでに紹介した演算子を組み合わせて,次のようにも表現出来るよなぁ. ラプラシアンを $\triangle$ で表記すると,微小量を表すときによく使うデルタと区別がつきにくくなる.慣れてくると文脈で判断できるものだけれども,初学者向けの解説を書くときにはなかなか気を遣う.いつも $\nabla^2$ を使うようにすればそのような問題は起こらないのだろうが,「この式の場合は是非とも $\triangle$ を使って書いた方が見栄えがいい」という場面があったりするのである.

組み合わせ

div と grad を組み合わせてラプラシアンが作れた.この他にも,すでに出てきた grad , div , rot の 3 種類の演算子を組み合わせることで何か面白い便利な関係が導けないだろうか.

grad はスカラーに作用し,ベクトルを作るのだった.また div はベクトルに作用し,結果としてスカラーを作る. rot はベクトルに作用し,その結果もベクトルである.ということは・・・,組み合わせられるパターンの数はそんなに多くなくて,試してみると次の 5 種類に限られることになる. 上から順番に試して行ってみよう.まずは grad div から. ああ,ダメだ.これは複雑な結果になるだけで何も面白くない.次はどうだ？いや,これはさっき出てきたとおり,ラプラシアンになるのだった.次の div rot はどうだ？なんと,0 になってしまう！この組み合わせの時にはが何であろうと常に 0 だということだ.では次. これも 0 になる.こちらはただの 0 ではなく,ゼロベクトルだ.意外と面白いものである.では最後の一つをやってみよう. 最後の行でシンプルにまとめたが,そこには少し注釈が必要だ.先ほどの説明ではラプラシアンはスカラーに対して作用するものだった.だからこそ,ラプラシアンと div grad は同じものだと言っても問題なかったのだ. grad はスカラーに対して作用してベクトルになり,その結果に対して div が作用するという意味だからだ.しかしここでは $\triangleA$ という表記が使われており,ラプラシアンがベクトルに対して作用している.その意味は,直前の形を見れば分かる.つまり,ベクトルの各成分に対してラプラシアンを作用させて新たなベクトルを作ることを意味している.これは特別ルールなので,これを代わりに div grad と書くことは避けるべきだろう.もしそうしてしまった場合,ベクトルに grad を作用させるという時点でワケが分からないことになる.

ここまでの結論をもう一度ひとまとめにしておこう.

0 になる理由

div rot と rot grad が 0 になることについて,単に計算結果がそうなるから,というのではなく,具体的なイメージで説明できないだろうか.

rot grad U=0 の方はこんな考え方が出来そうだ. grad U は 2 次元の地図に例えると,地面の傾斜の度合いと方向を矢印で表したものであった.この矢印の方向に沿って歩いて行くということは,どこまでも坂を登ってゆくことに相当する.このように矢印に沿って歩くとき,周辺をぐるりと回って,元の地点に戻って来ることは有り得ない.もしそのようなことがあれば,前と同じ地点に帰ってきたはずなのに,以前より高い場所にいることになってしまうからだ.つまりこの矢印は,ぐるりと輪を描いて戻ってくるようには決してなっていないはずである.どんなミクロな領域を考えても,どんな形の輪を考えても,矢印はそれに沿うようにはなっておらず, grad U には渦を巻くような要素は無さそうだ.

という説明を考えてみたものの,かなり感覚に頼っており,数値的な説得力に欠ける.

div rot A=0 の方はどうだろう？ベクトル場の中に渦を巻いた部分があると, rot A という矢印が現れる.それは途切れて消えることなく,またどこからも新しく現れることなく,どこまでもつながっているというイメージである.しかしなぜそのようなことになっているのかの説明は難しい. rot A というのは必ずしも「渦」のイメージではなく,並行する流れに流速の差さえあればどこにでも現れるものでもあるという点を考えると,さらに難しい.これについて色んな人から意見をもらったのだが,よくもまぁ,こんなに違ったイメージでの解釈が色々あるものだなと感心した.しかしそれらを説明するには前提知識の説明に時間が掛かるし,数学に近かったりするので,私の好みからは外れている.あまりイメージを固定しないで読者に任せる方がいいのかも知れない.