量子力学：CHSH不等式

準備

ベルの不等式というのは「量子力学が主張するような不思議な遠隔相互作用」を認めないような理論を作った場合に成り立っていなくてはいけない条件を示した式のことである.実験をしてみたらその式はやっぱり成り立ってなくて,量子力学の勝利！ということになったのだった.

今回紹介するCHSH不等式というのはベルの不等式の数あるバージョンの中の一つである.4 人の科学者の頭文字を取ってこう呼ばれている.

それがどのような不等式であるかを見せるのは後にしておきたい.ややこしい本題に入る前に,とりあえず今回の話に関係してくる次の式を証明しておこう. ただし,,,,はどれも実数で,その絶対値は1以下であるとする.第 3 項だけにマイナスが付いていて対称ではない感じだが,これは誤植ではない.

なるほど,試しに,,,に色々と数値を入れてみてもこの範囲を越えられそうにないわけだが,ちゃんと理論的に示しておきたい. この最後の式の第 1 項は (a+b) か -(a+b) であり,第 2 項は (a-b) か -(a-b) である.どんな組み合わせで和をとろうとも ±2a か ±2b になる.もも絶対値は 1 以下であるという仮定があるし,右辺は負にならないことははっきりしているから,最後の式の続きとしてはだと考えていいということになる.結局,これで (1) 式の証明が終わったわけだ.絶対値を使わない方が分かりやすい気がするので (1) 式を次のように書いておこう. この式は後で使うので,それまでしばらく忘れていてもらって構わない.

相関の度合いを数値化する

ペアで生まれた 2 つの粒子を互いに遠く離れた 2 つの測定器へと飛ばして,それぞれの場所で同時にスピンを測定することを考える.

ここで同時と言っているのは実は厳密に同時でなくても良くて,ただ,一方の測定の影響が光速で他方に伝わる前に測定を終わらせておきたいのである.光速以下の何らかの方法で互いに影響を与え合う可能性を排除しておきたいだけのことである.

さて,このような状況で,一方で行われた測定の結果と他方で行われた測定の結果には何か関係があるだろうか？

ある.すごくある！

例えば両者が同じ方向のスピンを測っている場合,一方が上向きという結果が出たならばもう一方では必ず下向きだという結果が出るに違いないからだ.しかしそれでは実験としては単純すぎて面白くないし,別にわざわざ量子力学を使わなくてもこのような現象を説明することはできてしまいそうだ.そこで,量子力学を使った場合と使わない場合とで結果の予測に違いが出そうな状況を考えてみることにしよう.

例えば,それぞれがスピンを測定する時の角度を,ランダムに変えてやったらどうだろう.その角度は測定の直前になって気まぐれに決めてやっても構わない.そうすれば相手がどんな角度で測定したかを知ることも出来ないし,相手がどんな結果を得たかを確実に言い当てることも出来なくなる.

それでも,後で双方の集めた結果を持ち寄って調べた時に,お互いの結果に何か関係がある証拠が見い出せるものだろうか.

お互いの測定結果の関係の深さを数字で評価できるように次のようなルールを導入してみよう.スピンの測定結果が測定方向に対して上向きだったなら +1,下向きだったなら -1 だと記録することにする.受け取る粒子の状態は毎回違っているから,測定方向を変えようが変えまいが,結果はいつも半々の確率で出てくる.だから多数の測定をした結果の平均を取ってみれば 0 になるに違いない.

そのような,全くデタラメに見える結果ではあるが,お互いの結果の積を取ったものの平均を考えてみてはどうだろう.お互いに同じ結果が出た時には積は +1 だし,違う結果が出たならば積は -1 である.多数の測定について平均を取ってやってプラスの値になっていれば,同じ結果が出やすい傾向があり,マイナスの値になっていれば反対の結果が出やすい傾向があることが読み取れる.0 だったなら,お互いに全く関係がなく,本当にデタラメだったということだ.このようにして計算される値のことを「相関」と呼ぶことにしよう.

状況を単純にして理論を作る

先ほどは測定の角度をランダムにしようと提案したわけだが,それではあまりに自由すぎて理論を作るのが難しい.そこで状況を単純化するために,両方の測定場所でそれぞれに自由に 2 つの測定角度を選んでやって,その 2 つの角度のうちのどちらで測定するかを毎回ランダムに変えるという形に制限してみよう.

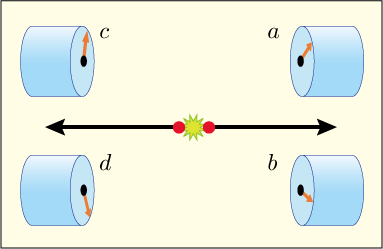
一方の測定装置では θ_a と θ_b ,そして他方の測定装置では θ_c と θ_d にする.そして多数回の測定を行った後で結果を持ち寄るわけだが,これは 4 種類のデータに分類される.つまり一方が θ_a で測定した時に他方が θ_c で測定していた場合,また,一方が θ_a で測定した時に他方が θ_d で測定していた場合といった具合だ.どの組み合わせの実験データも多数あるから,それぞれに平均を取って 4 通りの相関を計算してやることができる.

その計算は後でやってみることにしよう.量子力学を使えば何らかの相関があることが示せるのである.

しかしここでは一度量子力学のことは忘れて,このような相関があるような観測結果が得られるのは,もっと素朴で実在的な仕組みが背景にあるからに違いない,という考え方を試してみる.測定結果を決めるような隠れたパラメータが無数に存在しているかも知れないが,それさえ分かれば測定結果はいつでも特定できるだろうという思想だ.その無数のパラメータを $λ_{1},λ_{2},…$ のように表そう.その幾つかは粒子がペアで生成された時に,すでにそれぞれの粒子の中に隠された変数かも知れないし,粒子が測定器まで移動している最中に偶然に影響を与える何かを意味しているかも知れない.粒子の中に隠された変数は,移動中に変化しているかも知れないが,そういうことが起きていても構わなくて,全てはこれらのパラメータで表せると考えるのである.

そのような隠れた変数が取り得る値の組み合わせは無数にあるかも知れないが,その中の一つが実現する確率を $P(λ_{1},λ_{2},…)$ と表すことにする.おそらくは滅多に起きない組み合わせばかりになるだろうが,理論的なものだから問題ない.頻繁に起きることならそれだけ重要だし,起きなければそもそもあまり重要ではない要素だということだ.起こり得るすべての可能性を足し合わせれば,当然 1 である. この考えによれば,一方の測定器で θ_a の角度で測定した時に得られる結果はその角度とパラメータによって決まってしまい, $a(θ_a, λ_{1},λ_{2},…)$ と表せる.測定結果の平均を計算したければ次のように表せるだろう. これは先ほども書いたように 0 になるはずである.

それはさておき,さらに考えを進めよう.別の側にある測定器で θ_c の角度で測定した時の値は $c(θ_c, λ_{1},λ_{2},…)$ と表される.とにかく測定値は測定時の角度と隠れた変数によっていつでも確定するのであるという考えである.するとそれらの相関は次のように表されることになる. この値は -1 から 1 までの間の任意の実数値を取り得る.この式で使われている変数はやたらと多いけれども毎回書くほどの重要性は無いので,次のように略してみよう. これらは全て +1 か -1 のどちらかの値のみを取るのであり,これを使って ac+bc-ad+bd という計算をしてみれば,これは冒頭の (2) 式によって, であることがすでにはっきりしている.この (5) 式の全体に $P(λ_{1},λ_{2},…)$ を掛けて, $λ_{1},λ_{2},…$ のあらゆる可能性で積分してやれば,(5) 式の左右の -2 や 2 については (3) 式のような計算を行うことになり,-2 や 2 のままであり,他の各項については (4) 式のような計算を行うことになり,結局は次のような結果が得られる. 要するに, という幾つかの相関を組み合わせて作った謎の量を定義してやれば,はという範囲に収まるだろう,と主張しているのが「CHSH不等式」である.この無数の $λ_{1},λ_{2},…$ というパラメータはたとえ人間に把握し切れなくても,たとえ現実に観測可能な量でなくとも構わない.理論的に世界がそのように記述できる構造になっていさえすれば,この不等式を満たすはずである.

量子力学ではこの不等式が破れる

ではいよいよ,「量子力学を使ってこのという量を計算してやると,この不等式の範囲を越える結果が出てしまう」ということを示そう.

一方の観測で上向きの結果が出て,他方の観測でそれとはだけ角度をずらして測定した時にもやはり上向きという結果が出る確率は sin^2 (θ/2) なのだった.下向きが出る確率は 1-sin^2 (θ/2) である.実際にはどちらが先に観測したかは問題にはならない.粒子がペアで発生してまだ観測されていない状態というのは毎回異なった状態であるので,上が出るか下が出るかは半々である.どちらが出ようとも,とにかく,両方の測定器で同じ結果が出る確率は sin^2 (θ/2) であり,異なる結果が出る確率は 1-sin^2 (θ/2) である.同じ結果なら積は1であり,異なっていればであるから,それぞれに確率を掛けて足し合わせれば平均したことになり,相関が得られる. 例えば一方の測定器の角度が θ_a で他方の測定器の角度が θ_c だったなら, θ=θ_a -θ_c であるから, だということになる. cosθ は偶関数だから,だろうが, θ_c -θ_a だろうが結果は変わらず,気にしなくていい.というわけで,は次のように表されるだろう. 変数が 4 つもあるのでこの関数の振る舞いをイメージするのは難しく,最大,最小がどこにあるのかを探すのが難しそうだが, のように変数変換をして新変数の関係を探ってやれば, C=A-B+D という関係が成り立っていて,実は 3 変数の自由度しかないことが分かる. これで少しは調べやすくなる.第 3 項だけ符号がプラスになっていて,残りにはマイナスが付いているので,ひょっとして A=B=D=0 に選んだ時に最小値が実現するのではないかという期待を持ってを消去してみたわけだが,そんなに甘くはなかった.他の 3 つ項の値を -1 から少し増やすことになってでも第 3 項のプラスの影響を減らす方が,さらに小さな値が得られるようだ.

ここは常套手段ということで,極値の条件を試してみよう.極値ではどの変数が変化しても変化率が 0 になるはずなので,次の式が成り立っている. (6) 式から (8) 式を引いたり,(6) 式と (7) 式を足したりすることで sinA=sinD=-sinB という関係が得られ,もっとも単純な場合としては A=D=-B と考えてみても良いだろう,ということになる.念のためそれ以外の可能性も試してみたが面白い結果は出ないようである.とにかく,このようにすると sin(A-B+D)=sin3A であるから, sinA=sin3A という条件も得られる.これを満たすと言えば, の 3 通り,それと,これらをずつ増減させたものも当てはまる.この中で A=0 というのはさっきも考えてみたわけだが, S=2 にしかならず,どうやらただの停留点のようである.残りの 2 つを使った場合にはそれぞれ -2√2 と 2√2 であり,これらが最小,最大を実現しているようだ. この不等式を「チレルソンの不等式」と呼び, ±2√2 のことを「チレルソン限界」と呼ぶらしい.

修正履歴

(2024/01/19)
　・実験の説明図を追加.
　・式番号を入れて分かりやすくした.
　・(5) 式から次の式を得る過程を詳しく説明.