量子力学：1入力量子ゲート

ブロッホ球

すぐにでも量子ゲートの性質を説明し始めたいところではあるが,その前に量子ビットを視覚的に理解するための「ブロッホ球」という概念を説明しておく必要がある.なぜなら,量子ゲートの働きはこのイメージを使って説明されるし,各種の量子ゲートの名前もそのイメージを使って名付けられているものばかりだからである.

量子ビットは次のように表せるのだった. ただしこのとは複素数であり,しかも次のような条件が付いている. さらに (1) 式の全体に掛かる位相が違っていても物理的には同じ状態を表すというのだから,一体,そのように表される状態というのがどのような範囲をどう変化し得るのだろうかと,困惑してしまう.

複素数というのは 2 つの実数の組で表されているのだから,(1) 式には合計で 4 つの自由度がある.そこに (2) 式の条件と,が実数になるように位相を調整してしまってもいいという条件が入るのだから実質は 2 次元的な自由度だけを持っていることになる.数学的な話はすでに「ブロッホ球」という記事があるのでそちらを参考にしてもらいたい.

結論を言ってしまうと,量子ビットの状態というのは次の図に描かれるような球面上の一点で表されるのであり,他の状態へと連続的に移行するときにはこの球面を移動するかのように変化するのである.

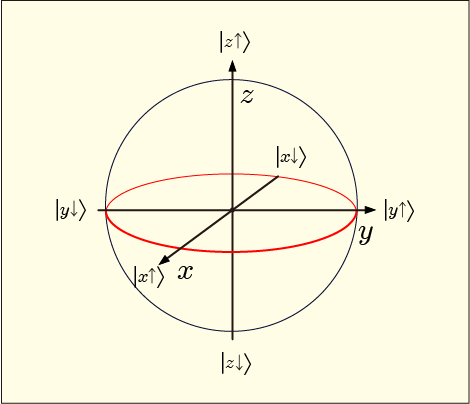
この図では,,の座標が描かれているし, |x↑>} や |y↓>} などの記号も使われていて,(1) 式とどんな関係があるのかよく分からないことになっている.実はこの図は電子のスピンの上向きと下向きの重ね合わせの状態である次のような式を元に作った図だからである. 量子コンピュータは電子のスピン状態に限らず,2 つの量子状態の重ね合わせを持つどんな現象を利用しても良いので, |z↑>} と |z↓>} をそれぞれ |0>} と |1>} になぞらえて解釈すればいい.

|z↑>} と |z↓>} というのはそれぞれ,電子のスピンの軸方向の成分を測った時に上向きになる状態と下向きになる状態を意味しており, |x↑>} や |y↑>} なども,他の軸方向の成分を測ったときの状態を意味している.そして,それらは次のような関係があるのである. この 1/√2 というのは規格化のために入れてあるものだからあまり気にしなくても問題ない.

とにかくこういうわけだから, |0>} と |1>} のことだけしか考えたくないと言うのなら,先ほどの図は次のように描き直したらいいだろう.

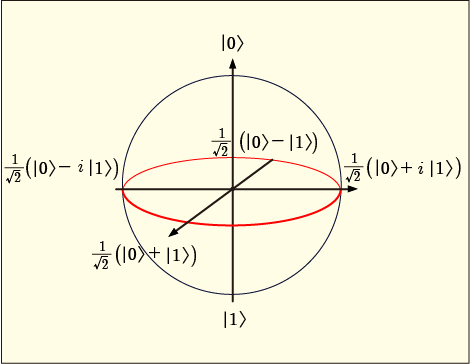
なぜわざわざ電子のスピンの話を経由させてここまで来たかというと,量子ゲートの中には,この電子のスピンのイメージ由来の名前を持つものがあるからである.

回転ゲート

量子ゲートは古典的な論理ゲートとは違って,入力の数と出力の数が同じものばかりである.その理由は次回あたりで話す予定である.今回は 1 つの量子ビットの入力に対して 1 つの量子ビットを出力するタイプのゲートの話に集中しよう.

そのような種類のゲートというのは,つまりゲートに入っていった量子ビットの状態が何らかの加工をされて出てくるのである.古典的な論理ゲートでは 1 か 0 かしかなかったので,1 を入れたら 0 を返すとか 0 を入れたら 1 を返すという NOT ゲートしかないのだった.ところが量子ビットの状態は先ほど説明したブロッホ球の表面のように広がる多様さがある.加工の仕方も一通りではない.

この球面上の様々な状態に対して何か共通のルールで加工することになる.ある状態に対してはこう対処して,別の状態のときには別の対処をして,というような複雑な動作は期待できない.量子ゲートというのは物理法則を利用したごく単純な操作の要素をブラックボックス化した概念だからである.

結論を言ってしまうと,ブロッホ球の中心を通る何らかの軸を中心にして,いくらかの回転をするというルールで,このタイプのゲートの動作を視覚的にまとめることが出来る.それで総称として「回転ゲート」と呼ばれることがある.また,「ユニタリゲート」と呼ばれることもある.状態どうしの内積を変化させない変換のことを「ユニタリ変換」と呼ぶが,球面上の状態が全体的に回転するような変換法則はこの条件を満たしているからである.

回転軸の方向と回転角をもっと具体的にしたものについて考えていこう.よく使われるものにはそれぞれの名前が付けられている.最初の方のブロッホ球の図の軸の周りに 180°の回転をさせるものを「Xゲート」と呼ぶ.同様に軸の周りに 180°回転をさせるものを「Yゲート」と呼ぶ.軸の周りに 180°回転をさせるものを「Zゲート」と呼ぶ.これらは 180°の回転をしているので「 $\color{red}{π}$ ゲート」と呼ばれることもある.また「パウリゲート」と呼ばれることもあるが,その理由はあとで話そう.

軸の周りに角度だけ回転させるものを「位相ゲート」と呼ぶ.回転方向は北極側から見下ろして左回転である.

また軸から軸へと向かう中間の 45°を軸として 180°の回転をさせるものを「アダマールゲート」と呼ぶ.これは「アダマール変換」というものを実現するゲートだからである.これも,詳しくは後で話そう.これはフランスの数学者ジャック・アダマール(1865-1963) に因んで付けられたもので,Hadamard という綴りなので頭文字の H がシンボルとして用いられる.

次に,それぞれのゲートを通したときに起こる変化の意味を見ていくことにしよう.

ゲートの作用を行列で表す

状態 |0>} と |1>} とは互いに直交するベクトルのようなものであるから,分かりやすいように,次のような単純なベクトルを当てはめて考えることにする. すると (1) 式のような重ね合わせ状態は次のように表せることになる. 量子状態の変化というのは,観測したときの突発的な変化以外はユニタリ変換で表せるものなので,様々な状態の変化はどれも行列で表せることになる.例えば,Xゲート,Yゲート,Zゲートのような変化はそれぞれ次のような行列で表せる. これらは電子のスピンを扱う時に出てくるパウリ行列と同じである.これらのゲートが「パウリゲート」と呼ばれる由来はここにある.

以上の話が本当に成り立っているかをちゃんと確かめてみると,計算の後で全体にややを掛けてやらないと図の通りにはならない場合があるということに気付くだろう.このブロッホ球の図は全体に掛かる位相の要素の違いは同一のものとしているから,これくらいの調整は許さないといけない.

XゲートやYゲートは |0>} を |1>} に, |1>} を |0>} に変えるので,古典的なNOTゲートに似たものとなっている.一方,Zゲートはといえば, |0>} や |1>} の確率の重みは変化させないが,互いの重ね合わせの位相を反転させている.

さて,なぜこのようにして行列をわざわざ導入しているかと言うと,ゲートを次々と通して行った時の状態の変化を行列の積で計算できて便利だからである.ゲートを通るたびに行列を左から掛けるのである.量子ゲートを並べて回路を描くとき,左から右へと状態が変化してゆくように書く約束になっているが,行列はどんどん左側に並べて積を作ることになるので,並べ順が互いに逆になっていることには気を付けないといけない.

位相ゲートは変数付きの量子ゲートであった.位相ゲートは行列で表すと次のようになる. |0>} と |1>} の重ね合わせの位相を $e^{iθ}$ だけ変化させている.ゆえに「位相ゲート」と呼ばれるのである.

アダマールゲートはどんな行列で表せるだろうか？実は分かりやすい法則があって,ブロッホ球の中心から (x,y,z) 方向に伸びる単位ベクトルを軸として180°の回転をするとき,その行列は次のように表せるのである. アダマールゲートの場合は軸の方向が x=1/√2 , y=0 , z=1/√2 なので,次のようになる. $\hat{H}$ という演算子の記号がハミルトニアンのようであるが,量子コンピュータ分野ではアダマールゲートを意味することが多い.この行列を使うととなる.特に a=1 , b=0 のときには,つまり,もともと純粋に |0>} だったものは, となり, |0>} と |1>} を半々の確率で含む状態になるし,もう一度通すと元に戻る.このような理由でアダマールゲートは大変良く使われるのである.

ここに出てきた行列は全てユニタリ行列であり,次の関係を満たしている. $\hat{U}^{†}$ は転置して複素共役を取るという意味で,右辺は単位行列である.暇なら確認してみるといいだろう.

アダマールゲートと位相ゲートさえあれば万全

位相ゲートを通す前後でアダマールゲートを使うことを考えてみよう.

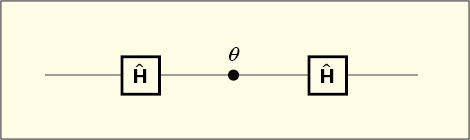
これらのゲートを順次通したときの変化を表す行列は次のようになる. これを |0>} に対して使うと次のようになる. 全体にかかっている位相 $e^{i θ/2 }$ は物理的には違いをもたらさないし,ブロッホ球の上でも区別されないので無視してもいい.省いてやろう. |0>} と |1>} の位相差が気になるのなら,さらにこのあとで位相ゲートを使って 90°回してやれば,次のようにも出来る. これはつまり,こういうことだ.もし θ=π なら |ψ>}=|1>} にすることが出来るし,の値次第でその中間のどんな比率の重ね合わせ状態にも持っていくことが出来る.位相の調整もできる.逆の操作をすれば,どの状態からでも |0>} に戻すことが出来る.

この二種類のゲートさえあれば,狙った状態を,どの状態へも移動させることが可能だということだ.だから量子コンピュータの実現のためには,少なくともこの二つのゲートを用意することが重要になる.

ここで少し疑問を持ったのだが,別にアダマールゲートでなくても,代わりに軸周りに 90°だけ回すようなゲートを使っても同じことが出来るのではないだろうか.実は可能である.2 乗して $\hat{σ}_y$ になるような行列を探して試してみるといいだろう.しかしアダマールゲートは 2 回通せば元に戻るが,このゲートは 2 回通すと反転してしまう.同じことをさせるには途中にはさむ位相ゲートで 180°余計に回してやらないといけなくて少し面倒なのである.

今回は 1 つの量子ビットの状態ならばゲートの組み合わせで自由に操ることが出来ることが分かった.次回は 2 つの入力と 2 つの出力を持つゲートについて説明することにしよう.それがあれば 2 つ以上の量子ビットを関係付ける操作が出来るようになる.