量子テレポーテーション

短いけどこれで全部

量子テレポーテーションというのは,遠く離れた場所へ量子ビットの状態を転送する技術である.あまり詳しい前置きは必要ないだろう.量子ゲートの知識があれば簡単に理解できてしまう.使うのはアダマールゲートとCNOTゲートだけだ.

次の図が,量子テレポーテーションを実行するための量子回路である.

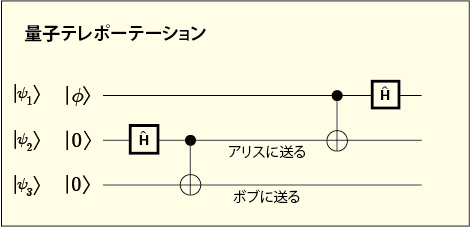
簡単に見えるが,本当に簡単である.一番上の量子ビット |ψ_1>} に,転送したい状態 |φ>} を入力する.上から 2 番目と 3 番目の量子ビットには初期状態として |0>} を入力することにしよう.

最初の 2 つのゲートで何が起こるかは実はもう以前に説明済みなのだが,もう一度説明しておこう. |ψ_2>} はアダマールゲートを通ることで, |0>} と |1>} の半々の重ね合わせ状態になる. 次にこれをCNOTゲートの制御ビット側に入れて |ψ_3>} を操るわけだが,「 |ψ_2>} が |0>} なので何も起きなかった状態」と「 |ψ_2>} が |1>} なので |ψ_3>} が反転して |1>} に変わった状態」との重ね合わせ状態が出来上がる. これはエンタングル状態であり, |ψ_2>} と |ψ_3>} の状態は別々には語れないような状態なのだった.つまりどちらかを観測して 0 なら他方も必ず 0 になるし,一方が 1 だったなら他方も必ず 1 が出る.そんな 2 つの状態が重なって存在している状態である.

この 2 つの量子ビットが絡み合った状態は,互いにどれだけ離しても切れることはない.というわけで |ψ_2>} の方をアリスに持っていてもらい, |ψ_3>} の方は遠く離れたところにいるボブに送るとしよう.

アリスとボブというのは情報分野や暗号通信に関する教科書や論文で良く使われる人物名である.頭文字がそれぞれ A と B だからである.多くの場合,アリスが送信側,ボブが受信側である.

ここまではエンタングル状態になった「双子の粒子」を作ってそれぞれを遠く離れた二人に持っていてもらうための準備作業であるから,もし同様のことができるのならばわざわざ量子ゲートを使う必要もないのである.量子テレポーテーションの本番はこれからである.

アリスは送りたいと思っている量子ビットをセットした |ψ_1>} と,手元にある双子の粒子の片割れである |ψ_2>} とをCNOTゲートに通す.この段階で 3 つの量子ビットが絡み合うことになるのだが,それを式で表してみたい.まず, |ψ_1>} の初期状態は |φ>} であり,次のように表しておこう. すると,CNOTゲートを通る前の 3 つの量子ビットを合わせた状態は,次のようになっていたわけである. そしてこのCNOTゲートは |ψ_1>} が |1>} の時に限って |ψ_2>} の状態を反転させるのだったから,状態を次のように変えるのである. このように絡まると,もう積の形には分解できまい.そして最後に, |ψ_1>} だけをアダマールゲートに通す.アダマールゲートというのは,次のように変換するものだと考えて良い. つまり,結果は次のようになる. かなり項の数が増えてしまった.ここで少し視点を変えて, |ψ_1>} と |ψ_2>} を合わせた状態が同じになっている項どうしでまとめてみよう. これをどう解釈してやろうか？もしアリスが手元にある |ψ_1>} と |ψ_2>} を観測してみて両方とも 0 が出た場合には,アリスは重なり合わさった 4 つの世界の中から第 1 項で表される世界を選んだのであり,その世界ではボブの手元にある |ψ_3>} は α|0>}+β|1>} という状態になっているということだ.これはアリスが送りたかった状態 |φ>} と同じものなので,アリスはボブに電話して「そのままでいい」と伝えればいいのである.

もしアリスが |ψ_1>} と |ψ_2>} を観測してそれぞれ 0,1 という結果を得たならば,ボブの方にある |ψ_3>} は β|0>}+α|1>} になっている.アリスはボブに電話して「その |ψ_3>} をNOTゲートに通して」とお願いすればいい.NOTゲートは別名 X ゲートだった.

1,0 という結果を得たならば,ボブが持っているのは α|0>}-β|1>} である.どういう指示を出したらいいだろう？そうだ.位相ゲートで 180°回してもらえばいいのだ.これは別名 Z ゲートである.

1,1 という結果を得たならば,ボブが持っているのは - β|0>}+α|1>} である.ここから元の状態を復元してもらうには,X ゲートを通してから Z ゲートを通してもらえばいいが,それは Y ゲートを通すのと同じことだ.

これで遠方まで量子ビットの状態を運ぶという目的は実行できる.これが量子テレポーテーションだ.

補足

アリスは送ろうとしていた |φ>} がどんな状態だったのかを知っていてもいいが,知らなくてもこの方法を行うことができる.もし知らなかったとしたら,最後まで知らないままである.アリス側の測定ではアリスは |φ>} についての情報を得ることはない.そしてその手元の量子ビットの状態は測定によって完全に壊れてしまうのである.

このようなわけで,量子ビットが複製されるということも起こらない.

あたかもアリス側にあった量子情報が一瞬で遠く離れたところへと飛んで行ったかのような結果であるが,量子ビットの状態を相手側で復元させるには電話による指示が必要である.よってこの情報伝達法が光速を超えることはない.

量子情報が空間のどこかを通って転送されたわけでもない.アリスとボブの持っていた双子の粒子の状態は最初からつながっており,アリスの測定が「アリスとボブを含めた全体」の状態の中から一つの可能性を選んだことになるのである.遠くの粒子の状態を一瞬で変えたのではなく,遠くの状態も近くの状態も含めて既に変わってしまっているような複数の世界の一つを観測によって選択したのだ.アリスは自分がどの世界に来たかを知った上でボブに指示を出す.それはあたかも世界そのものを使ったトリックという感じである.共犯者は,複数に重なり合った世界そのものである.

それにしても巧妙ではないか.アリス側にあったやなどの係数を,式をうまくくくってまとめることでボブの側の状態へと転嫁させてしまうのだから.アリスにとってはボブの存在もまた,やがて |ψ_3>} を観測して 0 を得ることになるボブと 1 を得ることになるボブとの重ね合わせなのだ.