量子力学：電子配置の確認

今回のテーマ

フント則を学んだので基底状態の電子配置に興味が出てきた.二つ前の記事の話を蒸し返すことにしよう.p 軌道に電子が 2 つ入っている場合には（LS結合のイメージが正しいなら,理論的には）次の 5 つのエネルギー準位が生じるのだった. そしてこの中で一番低いエネルギー準位は ^3P _0 である.

ところがこの ^3P _0 というのはフント則から素直にイメージされるような次のような電子配置になっているわけではないのだ.

	m=1	m=0	m=-1
α軌道 (s=1/2)	●	●
β軌道 (s=-1/2)

では一体どんな電子配置をイメージするのが正しいというのか？今回はそれを調べてみることにする.

復習

この作業のために二つ前の記事でも出てきた角運動量の合成結果の式に再登場してもらうことにしよう. これは軌道角運動量の合成であり,(1) ～ (5) 式が L=2 を表しており,(6) ～ (8) 式が L=1 ,(9) 式が L=0 である.スピンの合成の式も必要になる. (10) ～ (12) 式が S=1 であり,(13) 式が S=0 である.こういう話は面倒くさいと思う人もいるかも知れないが,私もまた面倒くさいと思っているのである.ちょっと覚悟が必要だ.

その前に,なぜこのような式が必要なのかについて再度説明しておこう.この p 軌道にある電子の個々の電子の軌道角運動量状態というのは (1) ～ (9) 式では |m>} で表されている. m=1,0,-1 である.ところがこのというのは軌道角運動量の軸成分を表しているだけであり,本当はどれも l=1 で表される軌道角運動量を持っている.向きが違うだけなのである.軸成分だけなら個々の電子のの値を合計すれば求められるが,全体としてどういう角運動量を持つことになるのかについてはそれぞれの位置関係（向きのこと）まで考慮しないといけない.あいにく,全軌道角運動量 $\color{red}{L}$ の値が定まる固有状態というのは個々の電子の固有状態とは共通していないことが,量子力学の理論から分かっている.それで,上のような複雑な組み合わせで全軌道角運動量が定まるような状態を表現することになるのである.

スピンについても m=1/2,-1/2 として考えればいいだけであって,理論的な内容は同じである.

L=0 かつ S=0 の場合

5 つのエネルギー準位のうちで最も簡単なのは ^1S _0 である.これは L=0 かつ S=0 を意味しているのだから,(9) 式と (13) 式を組み合わせて考えればいい. 6 つの項が出てきている.これをどう解釈するかだが,この各項は $|m_{A}>}|m_{B}>}|s_{A}>}|s_{B}>}$ のような構造になっている. $m_{A}$ と $s_{A}$ が電子 A の軌道角運動量とスピン, $m_{B}$ と $s_{B}$ が電子 B の軌道角運動量とスピンである.このままでは分かりにくいので,図示したいところだ.例えば最初の項は |-1>}|1>}|- 1/2 >}| 1/2 >} となっているが,次のように表せる.

	m=1	m=0	m=-1
α軌道 (s=1/2)	B
β軌道 (s=-1/2)			A

二つの電子を区別している辺りがおかしいと思うかも知れないが,問題ない.その理由を説明しよう.一番最後の項に目を移すと - |1>}|-1>}| 1/2 >}|- 1/2 >} となっており,これを図示すると次のようになる.

	m=1	m=0	m=-1
α軌道 (s=1/2)	A
β軌道 (s=-1/2)			B

先ほどの配置と比べると電子を入れ替えた形になっている.しかも項の符号が逆になっている.どの項を見てもこのように他の項と対になっており,電子を入れ替えると全体の符号が逆転するというフェルミオンの性質が数式として反映されているのである.

毎回このような表を書くのは面倒なので,今後は符号が正になっている項だけを次のような簡略化した図で表すことにしよう.

符号が負になっている項はこの図の A と B を入れ替えた形になっているのだから省略してやることにする.この表し方を使えば,先ほどの式は次のようにまとめて書ける.

このような調子で他のエネルギー準位の状態も表していくことにしよう.

L=2 かつ S=0 の場合

次に簡単そうなのは ^1D _2 である.これは L=2 かつ S=0 のことなので,(1) ～ (5) 式と (13) 式の組み合わせである.つまり,5 通りの状態が得られることになるわけだ.しかしわざわざ 5 通りの式を書くのは面倒である.負の項が出てくる原因は (13) 式だけにあるので,それを省いて考えることにして,数式を経ずに図示するところまで行けるだろう.

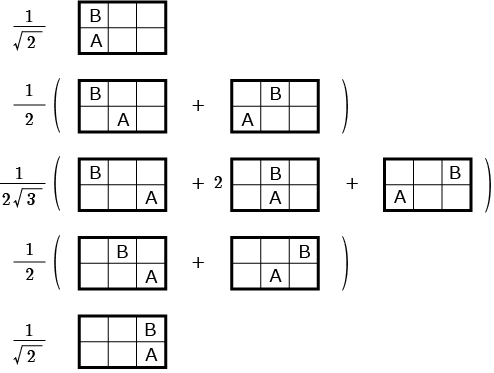
これら 5 つの状態は向きが違うだけの実質的に同じ状態なのであり,これらの状態の任意の重ね合わせ状態が ^1D _2 というエネルギー準位を構成している.

L=1 かつ S=1 の場合

一番厄介なのは ^3P _0 , ^3P _1 , ^3P _2 の 3 つの準位である.これらはどれも L=1 かつ S=1 であるから (6) ～ (8) 式と (10) ～ (12) 式を使うことになるのだが,単純に全ての組み合わせを作ればいいわけではない.

今からやろうとしているのは L=1 と S=1 の角運動量の合成である.これは l=1 である電子 A と l=1 である電子 B の角運動量の合成をするのと理論的な内容が変わらないので,(1) ～ (9) 式と同じ形の結果を得ることになるだろう.(1) ～ (9) 式の右辺には $|m_{A}>}|m_{B}>}$ という形の多数の項があるが,この m_A が |1>} となっているところには (6) 式を, |0>} のところには (7) 式を, |-1>} のところには (8) 式を代入する.同様に m_B が |1>} となっているところには (10) 式を, |0>} のところには (11) 式を, |-1>} のところには (12) 式を代入する.そういう入れ子的な置き換え作業を黙々とこなすという面倒くさい手術が必要になる.

頑張ってここに途中式を書いてみても読み飛ばされるだけだろうから,結果だけを書き並べてみることにしよう.この展開作業中に一つ気付いたことを言っておくと,複数の項が打ち消し合ったりまとめられたりすることは一切なかった.それぞれ少しずつ違う項の掛け算なのだから,結果を知ってしまえば共通項が存在しないのも当然のことだと思えるのだが,実際にやってみるまではそうやって式が簡単になったりすることもあるのではないかと期待していたのだった.要するに,共通項を括り出すといったテクニック的なことは一切必要なく作業は進むので安心してほしい.

まずは J=2 となる 5 つの状態からだ.

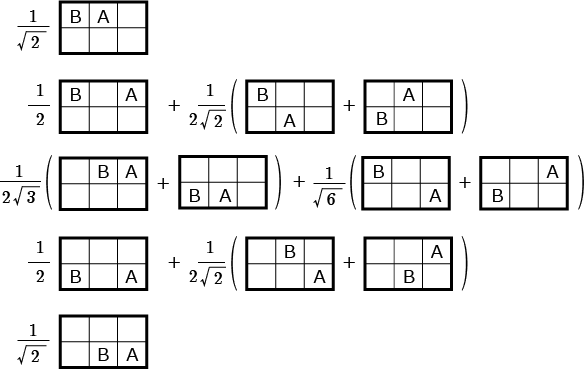
これらは ^3P _2 に相当する.どれも同じエネルギー準位であり, ^3P _2 はこれら 5 つの状態の任意の重ね合わせから出来ている.

次は J=1 となる 3 つの状態を計算してみよう.

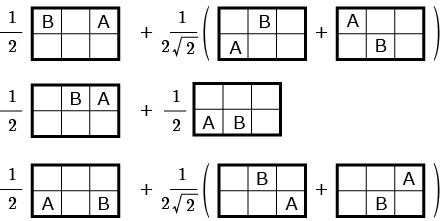
これらは ^3P _1 に相当する.どれも同じエネルギー準位であり, ^3P _1 はこれら 3 つの状態の任意の重ね合わせから出来ている.

最後に残ったのは J=0 となる 1 つの状態である.

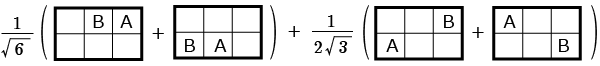
これは ^3P _0 に相当する.状態は 1 つしかないので任意の重ね合わせ状態というのはない.

結果を見て思うこと

フントの規則によると基底状態は ^3P _0 である.つまり現実に起きる電子配置は一番最後に求めた形のものであって,フント則から素朴にイメージするような配置とは全然違っていることが分かる.

ではなぜ前回やってみた方法でとが正しく求まるのだろうか？フント則から素朴にイメージする状態というのは,先ほどの計算結果の中から探してみてほしいのだが, J=2 となる 5 つの状態の中の最初の一つである.つまり,が幾つのものが本当に基底状態になるかというのはとりあえず判断から外しておいて,フェルミオンの性質を考慮して実現可能な状態の中から,とが最高状態になるような組み合わせをとりあえず探したのである.「ずる賢い術」と呼んだのはそういうわけである.

リー群論の言葉を借りれば,最高ウェイトがどうなるかだけを真っ先に考えたことになる.現実の物理を無視して結果だけに飛びつく姑息な解法なのであり,実際に起きていることのイメージとも大きく違っている.

なぜこのようなごちゃごちゃと重なった状態が基底状態になるのだろうか？先ほどはやが確定した状態というのは重ね合わせ状態でないと表せないのだという話をした.そこからさらに上の段階があって,とを合成した全角運動量というのはやが確定した状態を重ね合わせないと得られないということになっているのである.

ではなぜ最終的にが確定した状態になって落ち着くかと言えば,との相互作用でエネルギーが定まるようなモデルを採用して計算しているからであり,の違いはエネルギーの違いを表すのに都合が良かった.そして実際に,そのようなモデルは現実をある程度正しく表せているようである.原子は光を放って最低エネルギー準位へと落ち着くわけだから,エネルギー値が確定した状態を目指すというわけである.

さて,このような計算をしてみてもまだ分からないことがある.このような多数の状態の中でなぜ ^3P _0 が最低エネルギー準位を取ることになっているのだろうか.計算結果から何かヒントが読み取れるかと期待していたのだが,スピンの方向が揃っているようにすら見えない.この辺り,かなり慎重に検討する必要がありそうだ.