量子力学：スピンとは何か

磁気モーメントの測定

かなり後になってしまったが,原子が持つ角運動量を測定する方法の一つを紹介しよう.

まず,小さい穴の開いた容器の中に調べたい物質を入れて,加熱する.するとその物質は蒸気となって穴から噴き出すだろう.酸化を防ぐためにも真空中で行った方がいい.

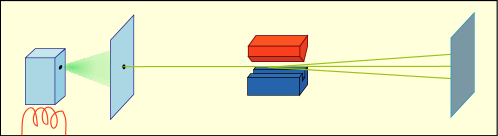
その穴から少し離した所に衝立を置いて,そこに小さい穴を開けておく.こうすることで,容器の穴から衝立の穴まで真っ直ぐに飛んできた原子だけが通過を許されて,穴を抜けた原子はその後も真っ直ぐに飛び続けることになる.こういう働きをする衝立を「コリメータ」と呼ぶ.「平行になるように整える装置」くらいの意味だ.こうして一本の原子のビームが作られるわけだ.この装置を真空中に置く本当の理由は酸化防止よりもむしろこちらである.障害物となる気体があっては原子は真っ直ぐに飛べない.

このビームの進路上に磁場を働かせてやると原子の持つ磁気モーメントが磁場と作用して,原子が進路を曲げることになる.ただしここで一工夫が必要である.普通の磁場では曲がらせることはできないのだ.

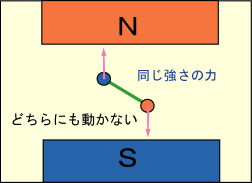
もし電子のビームならば電場の中を通せば進路は曲がる.同様に,もし磁気モノポールというものがあったとしたら,それを磁場の中に通せば同じように進路は曲がるだろう.しかし磁気モーメントというのは,異符号の磁気モノポールが棒で繋がったようなイメージのものである.一様な磁場の中ではその両端がそれぞれ反対方向へ同じ大きさの力を受けることになり,どちらへも動かないことになる.

ではどうすれば良いか.一方へ近付くほど強い磁場が掛かるようにしてやるのである.例えば次の図のような断面の磁極を作ってやればいい.

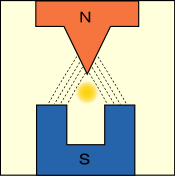
オレンジ色に塗った部分に注目すると,下へ行くほど磁力線が広がって疎になるので磁力は弱くなるというわけだ.磁力線の様子はあまり正確ではないので信用してはいけない.こんな凝った形状にしなくても次のようなものでもいいようだ.

このような磁場の中では磁気モーメントはすぐに向きを変えてしまうのではないのか,という心配は無用である.確かに磁気モノポールが 2 つくっ付いたものなら,磁場の向きに従う方がエネルギーが低いので,向きを変えて,余ったエネルギーを光として放出してしまうだろう.しかし原子の磁気モーメントの原因は電子の角運動量であり,角運動量保存則がある限り勝手に向きを変えてしまうなんてことは起こらないのである.

追記(2022/04)：ここの議論には間違いがある.角運動量保存の法則は空間の向きの対称性に起因する法則であり,この状況では外部磁場が掛けられていることによって対称性が崩れており,角運動量保存則が成り立っていない.古典力学的にもこのような状況ではコマの歳差運動のような角運動量のふらつきが起きる.似たようなふらつきがスピンでも起きているはずである.しかしふらつきが起こるだけなので,磁気モーメントが容易に磁場の方向へ変化してしまうわけではないという話の筋については問題ない.

ただし,磁場中で他の粒子と衝突したときに,角運動量を相手に与えることで,磁気モーメントの向きを変える現象は起こり得る.しかしこの実験が真空中で行われていることを思い出してもらいたい.そのような衝突はそれほど頻繁には起こらない.その頻度についてはきちんと計算されており,誤差として評価される.物理実験というのは,昼過ぎの奥様向けテレビ番組で行われているような子供騙しの実験とはレベルが違うのである.

こうして進路を曲げられたビームがたどり着く先にガラス板などを置いてやると,多数の原子はこれに張り付いて,吹き付け塗装をしたようになる.後でこの板を取り出して良く観察してやれば,原子がどのように進路を曲げられたかが分かるわけだ.

シュテルン・ゲルラッハの実験

上で説明したような実験は 1922 年に銀原子を使って行われた.「シュテルン・ゲルラッハの実験」と呼ばれる有名なものだ.この実験によって,とても不思議な結果が得られることになった.

結果について話す前に,この実験が行われた背景を説明しておこう.科学の歴史というのは必ずしも分かり易い順序で発展してきたわけではない.この実験が行われた年はまだシュレーディンガー方程式が発表される数年前であり,これまでに説明してきたような波動関数のイメージはまだ出来ていなかった.

しかし原子が飛び飛びの値の角運動量を持つことについては,この頃までに高度な理論が出来ており,スペクトル線の観察と合わせて,かなりの事が明らかになっていたのである.ただ量子力学に比べてそれほど洗練されていなかった,というくらいのもので,スペクトル線の説明についてはわずかな謎を残していただけだった.

だからこの実験は,原子の角運動量を測るという意味では理論の確認に過ぎず,当時提唱されていた「方位量子化」が現実に起きていることを分光スペクトルの解析以外の方法でも確かめようと意図したものだと思われる.ところがそこで意外なことが起こった.銀原子のビームは上下の 2 本に分かれたのだ.

何が意外なのか.銀の電子配置についてはスペクトル線の解析から見当がついていた.原子番号は 47 番で,47 個の電子の内の 28 個は M 殻を全て埋めており,残りの 19 個は N 殻の s, p,d 軌道を埋めて 1 つ余る.この余った電子は 4f 軌道ではなく,5s 軌道に入ることが知られている.記号で書けば次のような感じだ. カッコ内が軌道を表しており,右肩の数字がそこに入っている電子数を表している.つまり N 殻までに納まった電子は角運動量を互いに打ち消しあって 0 になっており,さらにそこからただ一つ飛び出した軌道の電子でさえ l=0 の状態にあるわけだから,全体としても角運動量を一切持たないはずなのだ.

ところがこの結果は一体どういうことか？角運動量を持たないはずのものが,磁気モーメントを持っているとは！しかも上下に 2 通りのみ.

この現象はここまでシュレーディンガー方程式を使って考えてきた我々にとっても説明できないことだ. l=0 なら角運動量を持たないので当然ビームが分かれたりしないが,その次に許された l=1 の場合でさえ 3 つに分かれるはずなのだ.2 つにだけ分かれるというのはここまでの理論には出てきていない.

電子はスピンしている？

この現象が起きる理由について誰も全く見当が付かないわけではなかった.物質の磁性の原因は「電子の自転運動」によるのではないか,という考えはこの実験の少し前から出始めており,やがてこのイメージは 1925 年にハウシュミット (Goudsmit) とウーレンベック (Uhlenbeck) の論文により「スピン」と呼ばれ始めた.当時は電子を波動として捉えるイメージはまだなく,実在する粒のようなものを考えていた.電荷はその粒の表面に分布していて,それが回転することで磁気モーメントが生じるのではないかという説である.

今回の実験で見出された謎の磁気モーメントの原因は,殻外に一つだけ飛び出した電子のスピンに因るものであろうというわけだ.スピンに右回転と左回転の 2 種類があることを仮定すればビームが 2 つに分かれたことを説明できそうだ.N 殻までの電子はスピンが互いに逆を向く形で 2 つずつペアを作って納まっており,磁気モーメントを打ち消し合って観測に掛からないのだと考えられる.そして今回のように一つの電子だけが単独で余る場合にだけ,そのスピンが観測に掛かるというわけだ.

しかしこの説明には疑問が沢山ある.なぜ 2 つにしか分かれないのか.右回転と左回転があるのはいいとしても,回転の度合いは幾つもあっていいはずだ.自転が止まっているような状態はないのだろうか.

それに電子を大きさのある粒だと考えた時の致命的な問題は,その表面の回転速度が光速を超えてしまうということである.原子核の周りを回る電子の速度でさえ古典的に考えれば光速にかなり近いことになるので,それより小さい半径で回転しようとすればすぐにこの制限にぶつかるだろう.だから多くの学者は敢えてこの説を口にしなかったようだ.

先の二人は若い研究者であって,表面速度が光速を超える問題があることを知っていたが,相談を持ちかけたエーレンフェスト先生によって勝手に論文を投稿されてしまうのである.まさに生贄だ.参考リンク：「量子力学の歴史」４章, 1925年秋のところ

この辺りの問題に触れるのを避けつつ,何とかして理論化しないといけない.

理論化への一歩

さあここで,前回までに考えてきた角運動量についての数学の出番だ.方位量子数がの時,磁気量子数は 2l+1 個の状態が考えられるのだった.今は状態の数は 2 個しかないのだから,同じルールを適用すれば, 2l+1=2 より, l=1/2 とすれば良いのではないだろうか？実際これはうまく行って,角運動量と全く同じ理屈がそのまま当てはまる.磁気量子数は l～-l の範囲であって,1 ずつ増減したものが存在する.つまり m=+1/2 と m=-1/2 の 2 つの状態のみが考えられるのであり,現象をうまく説明できそうだ.

しかし磁気量子数が ±1/2 だというのは一体何を意味するのだろう.が整数でなければならないことは,波動関数が原子核の周りを一周したときに同じ値で繋がらなくてはならないという条件で導かれたのだった.しかし m=±1/2 となると,波動関数が 2 周してようやくつながるような条件を課したときに出てくる値ではないか.もしそのような条件を許すなら, m=±3/2,±5/2,±7/2,… などという値だって出てきてもおかしくないはずだ.

だからこれは原子核の周りの「軌道角運動量」とは別に議論されるべき何かなのだろう.論理は似ているかも知れないが,これはどこか別のところを回っているものだと考えた方が良さそうだ.それでこれを「スピン角運動量」と呼んで区別しよう.いや,ちょっと待て.その前に,これを本当に角運動量だと考えてしまっても良いだろうか？

パウリはこの謎の磁気モーメントの原因をスピンと呼ぶことを良しとせず,長い間「第 4 の量子数」と呼び続けた.これは賢明な態度だと思う.どこをどう回っているのかさえはっきりせず,ましてや自転だなどと断言できる根拠は何も無いのだから誤解を招く表現は避けるべきだ.実際,電子が自転していると信じてしまっている現代人の何と多いことか.「スピン」なんてのは今となってはユーモア混じりの表現であって,他に呼びようがないからそう呼ばれ続けているだけだ,と思った方がいい.しかし性質が分かってくると,これがなかなかうまい命名だと思えたりもする.

ランデの g 因子

軌道角運動量と同じ理屈を適用すると,スピン角運動量の値は ±ℏ/2 であるということになりそうだ.するとスピンが作る磁気モーメントというのは通常よりも小さいのだろう.私は前に電子の作る磁気モーメントの基本単位は「ボーア磁子」であると説明したが,「本当はボーア磁子の半分の値こそが基本単位だ」と書き直しておく方が無難なのではないだろうか.

ところが不思議なことにそうはなっておらず,スピンが作る磁気モーメントは,以前に定義した「ボーア磁子」と同じ値になっているのである.

これは困った.なぜって,以前の「角運動量と磁気モーメントの関係式」が成り立っていないことになる.そこでこの式に少しだけ細工しておこう. ここで付け加えられた g を「ランデの g 因子」と呼ぶ.g というのは「Gyromagnetic」の頭文字だそうだ.通常は g=1 だが,スピンの場合はなぜか g=2 になると言っておけば,数式が事実と違うという問題を回避できる.ああ,何たる小細工.

いや,少し弁護しておくと,これは量子力学が確立する以前に,観測結果を理論化しようとする真面目な議論の過程で導入されたパラメータであって,あからさまに小細工しようとしたわけではない.結果としてそのようになってしまっただけである.ランデ氏がこんな小細工を発表しただけで有名になれたはずがないだろう.

しかし不思議なものだ.スピンが磁気モーメントとして通常の 2 倍の効果を及ぼせるのはなぜなのだろう.やはり波動関数が同じところを 2 周回ってようやく繋がるというイメージと関連しているのだろうか.そんなことは勝手に幾らでも言えるが確かめようがないし,役に立たないのである.我々は波動関数がどういう仕組みで磁気モーメントを作るのかという具体的な構造を知っているわけではなくて,今のところ,ただ数式上,どんな関係が成り立っているかを確認できるだけだからだ.

注：g = 2 となる理由は全くの謎というわけではない.計算によって理論的に導くことができるので,別の記事で紹介しようと思う.

アインシュタイン・ドハースの実験

ところでスピンの角運動量は本当に ±ℏ/2 ということでいいのだろうか.シュテルン・ゲルラッハ型の測定は磁気モーメントを測っているのであって,角運動量を直接測っているわけではない.本当は g 因子などというものは余計で,スピン角運動量はだということはないのだろうか.

その疑念を拭うような実験があるので紹介しておこう.それは 1915 年に行われたものであり,スピンの概念が現れる遥か以前のことであるから,純粋に磁気モーメントと角運動量の比を測定する実験であった.

実験内容は簡単なものである.磁性体の円盤に磁場を掛けておいて,円盤を静止させ,いきなり磁場を切ると円盤は勝手に回りだすのである.逆のことをしてもいい.静止した着磁していない磁性体の円盤にいきなり磁場を掛けると,やはり円盤は回り始めるのである.これを「アインシュタイン・ドハース効果」と呼ぶ.

なぜこのような事が起きるのだろうか.まず,磁場が掛かっている時には円盤磁性体中のスピンはみんな磁場に対して同じ方向を向こうとして,向きが揃っている.つまり全体として磁場に平行な向きの大きな角運動量が作られていることになる.

注：なぜ「磁場に平行」などというもったいぶった表現を使うかと言うと,電子の電荷が負であるために,スピンの向きと磁気モーメントの向きが逆だからである.「磁場と同じ向き」と言って良いならどんなに説明が楽だろうか.

その後,磁場が消え失せてしまうと,スピンは互いに同じ方向を向いているより,バラバラな方向を向いた方がエネルギーが低くなって安定していられる.つまり,スピン角運動量は互いに打ち消しあって全体の角運動量は 0 になってしまう.この時,角運動量保存則を満たすためには,円盤全体が回らなければならないのである.

しかし「角運動量が保存しなくてはならないから全体が回る」だけでは説明になっていない気がする.それは結果であって,そのようになる理由があるはずだ.このことについて掲示板で相談したところ,スピンが方向を変える時の磁気モーメントの変化によって誘導電場が生み出されて,それにより回るのではないか,というところで落ち着いた.

面白そうだからこの現象を試してみよう,という人がいるかも知れないが,これは非常に検出の難しい微妙な効果であることを注意しておこう.

なぜなら,例えば 1 $cm^{3}$ の金属の質量は 10 g 程度だ.原子量が 50 程度だとすると, $10^{23}$ 個程度の原子からできていることになる.1 個の原子が程度の角運動量を持っているとして,全体では $L=10^{-34}×10^{23}=10^{-11}$ 程度にしかならない.半径 5 mm 程度で質量 10 g の玉っころの慣性モーメントは $I=(2/5)Ma^2 =(2/5)10^{-2}(5×10^{-3})^2 =10^{-7}$ であるので, L=Iω より,は $10^{-4}$ 程度と見積もられる.1 日かかってようやく一回転するくらいの勢いだろうか.

だから検出感度を上げるために工夫が必要である.同じ角運動量を生じるなら,円盤の半径は小さい方がいい.それで円盤というよりは円柱状にした試料を使う.さらに,試料を吊り下げた糸に鏡を付けて,そこに反射した光が遠くの壁を移動する様子を観察して回転角を測るのである.

この実験により,ランデの g 因子はほぼ 2 であることがはっきりする.実はこの実験は,スピン角運動量の大きさが ±ℏ/2 であることを示したというよりは,むしろ逆に,強磁性体の磁力の原因が軌道角運動量によるものではなく,ほとんどスピンによるものであることを示したという意味合いで取り上げられる事の方が多い.

とにかくこの実験によって,スピンが角運動量保存則を満たしており,物体のマクロな回転にまで影響を与えるような存在であることが分かる.スピンというのは理論形式上だけの話ではなく,確かに「角運動量」の一種であることが確認できるのである.

スピン行列

どうもイメージがはっきりしないので,何か新しい事が分かるまでは数式による理解を優先しよう.

角運動量を行列で表した時のやり方に倣ってスピンも行列で表してみよう.スピンには上向き,下向きの二通りの状態しかないのだから,これらを独立な単位ベクトルを使って, と表すことにする.そして,方向に測ったスピンは ±ℏ/2 という観測値として得られるので, という行列を作ってやれば, という関係を成り立たせることが出来る.では方向や方向にスピンを測定した時の値はどうなるのか.それを知るための行列 $\hat{s}_x$ , $\hat{s}_y$ は前回と同じ手法を使って求めればいい. $\hat{s}_x$ の固有値や固有ベクトルがどうなるかを計算してやると, となり,軸以外の方向に測ってもやはり s_x =±ℏ/2 という 2 通りの観測値のみを得ることになる.軸の場合にも同じようになる. これらのスピン行列には ℏ/2 ばかりが出てきて鬱陶しいので,それらを取っ払った行列を使う事にしよう. 見た目がすっきりしたお陰で精神的にかなり楽になった.この形の行列を「パウリのスピン行列」あるいは「パウリ行列」と呼ぶ.これを使うと固有値として ±ℏ/2 ではなくが出てくることになるが,理論形式自体が変わってしまうことはない.スピンの観測値はいつでも ±ℏ/2 であるという事さえ忘れなければ,この方が本質だけが見えて遥かに便利だ.パウリ行列は次のような交換関係を満たしている. 以前の交換関係の式からが消えた代わりに 2 が付いてきた.何もかも消えてすっきり,とは行かないようだ.

スピンの向き

スピンをイメージする時の注意を述べておこう.スピンの向きは「上向き」「下向き」と表現されることが多い.たとえ測定装置を横に向けて実験しても,「右向き」「左向き」とは呼ばれない.「上向き」「下向き」は実際の上下とは関係なく,そういう用語として使われているのだと理解してもらいたい.

上向きとか下向きとか言うけれども,完全に真上や真下を向いているわけではない.それは測定した方向成分についてだけを指して言っているのである.前の角運動量の時のイメージを思い出してもらいたい.スピンベクトルの全体の大きさは L^2 =l(l+1)ℏ^2 =(3/4)ℏ^2 であり,本当は次の図のような傾きがあるのである.

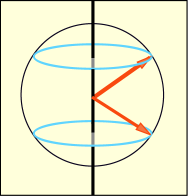
だから先ほどの「アインシュタイン・ドハースの実験」のところで行った説明は非常にきわどいごまかしをしているのである.本当はスピンは磁場に平行な向きを向いて揃っているわけではない.正しくは,「磁場の方向に対して皆同じある角度を保って,おおよそ同じ方向を向きながらも,バラバラな方向を向いている」と表現すべきだったのである.しかしあの場面でこのようなややこしい表現を使ったとして,その意味を理解できる人はどの程度いただろう.次のような図を描けば良かっただろうか.

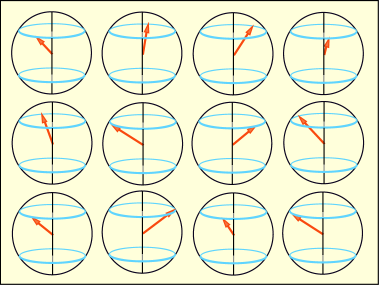
磁場の方向成分についてだけ言えば,皆そろっていたということである.しかし磁場が掛かっていない場合にはどっちを向いていたって構わない.本当にバラバラな方向を向いているのであって,中には真上や真下を向いているものもあるだろう.

追記(2024/01)：数式から得られるイメージは以上で説明したようなものではあるが,このようなスピンの向きが測定によって得られることは決してない.理論を何とか解釈しようとして出てくるイメージを,あたかも見てきたかのように,実際にそうなっているかのように説明してしまうのはあまり良いことではないかもしれないと思うようになった.

追記(2024/01)：スピンの「z軸に対する向き」が二つの方向のどちらかに限定されるというイメージから,このことを「方向量子化」と呼ぶことがある.しかし最近はあまり強調されないし,やめた方がいいのかもしれない.ここで言っているスピンの向きというのは,後に出てくるブロッホ球のイメージとは別である.

感想

以上がスピンについて「分かっていること」と「分かっていないこと」の基礎知識である.世間では「私は本当はもっと知っているけれども一般の人には分からないだろうから,配慮してわざといい加減な説明をしています」という態度の解説をよく見かけるが,知りたい根本の部分がごまかされていてストレスが溜まることが多い.しかし今回の記事を読んで感じてもらえただろうか.学者にとっても根本の部分は謎なのである.

しかし学者の立場を擁護するために言っておく.具体的なイメージを放棄しさえすればこれほど明らかな論理があるだろうか.具体的なイメージはそれほど大事だろうか.日常の生活に慣れてしまって,全ての物事に「具体的な構造」があるはずだと勘違いしてはいないだろうか.それらはみんな「在るように見えている」だけ……錯覚なのだ.

修正履歴

(2022/04/08)
　・角運動量保存があるのでスピンの角運動量も勝手に向きを変えてしまうことはないと書いていた部分に修正コメントを追加.

(2024/01/13)
　・スピンの向き（いわゆる方向量子化）の説明が不適切かもしれないことについて補足コメントを追加.
　・方向量子化という用語とブロッホ球について補足コメントを追加.

(2024/01/14)
　・2022年に追加したコメントが分かりにくかったので最後の一文を追加.