量子力学：時間発展演算子

ハミルトニアンが時間を含む場合

前回はハイゼンベルク描像について,「ハミルトニアンが時間を含まない」という特殊な場合に限った説明をしたのであった.では時間を含む場合にはどういう式変形で説明したらいいだろうか.

最初はちょっと面倒になりそうだと感じていたが,ここまで来たらとても簡単に話が進められると気付いた.細かな注意点はあるのだが,それは後回しにしよう.とにかく,次のようなシュレーディンガー方程式から出発することにする. 前回も同じところから出発したが,少しだけ違うのは, $\hat{H}$ が時間を含んでいるということである.ちょっと復習だが, $\hat{H}$ が時間を含まない場合には,この解は次のように表されるのだった. つまり,時刻 $t_{0}$ における状態 $|ψ(t_{0})>}$ に対してという演算子を作用させることにより,時刻における状態が導かれるというのである.さて,そこで思うのだが,今回の (1) 式の解についてもこれと同じように,(2) 式とは違う形の何らかのユニタリ演算子 $\hat{U}(t)$ を使って, という形で表されるのではないだろうか.なぜなら,ある状態から別の状態への変換は,ユニタリ変換で表されるからである.ユニタリ変換というのは,複素ベクトル空間の中で,ベクトルの長さを変えない変換なのだった.その物理的な意味は,粒子の全存在確率を変えないということであった.

このような $\hat{U}$ を「時間発展演算子」と呼ぶ.前回はわざわざ言わなかったが,(2) 式も時間発展演算子のひとつである.(2) 式の $\hat{U}$ がユニタリ行列であることはすぐに確認できる.

ここまで納得したら,(3) 式を (1) 式に代入してやればいい. この左辺を見ると,時間微分は $\hat{U}(t)$ の部分のみに作用する. $|ψ(t_{0})>}$ の部分にはが含まれていないからである.こうして両辺を比べてみると,どちらも同じ $|ψ(t_{0})>}$ に作用するのだから,両辺の演算子の関係は次のようになっていると言えるだろう. さあ,これを解いてやれば $\hat{U}(t)$ の形を知ることができるだろう！時々刻々と $\hat{H}$ は変化するのだが,その時々における $\hat{H}$ の効果を取り込みながら,こつこつと秒後まで足し合わせればいいのだ.両辺を積分してやればいい. t=0 において, $\hat{U}(t)$ は状態を何も変化させないという意味の演算子でなければならない.つまり $\hat{U}(0)=\hat{1}$ である.正しくはこのように $\hat{1}$ と書いて,これが演算子だということを忘れないように区別すべきだが,ちょっと過装飾っぽいし,多分忘れないと思うので今後は単にと書くことにする.それと,今後のために,積分の変数のと,積分範囲を表すをはっきりと区別しておいた方がいいので,ととでも書き分けておくことにしよう. さあ,望んだことはこれで果たされただろうか？いや, $\hat{U}(t)$ を知りたいのに,右辺にも同じ関数 $\hat{U}(t')$ が入ってしまっているではないか.うまくは行かないものだ.それで,ちょっと無茶な処方を実行しよう.この式の右辺の $\hat{U}(t')$ の中に,再びこの式全体を代入してしまうのである. これまで単に $\hat{H}$ と書いてきたが,どの時刻変数に従って変化するのかをはっきり示す必要が出てきたので, $\hat{H}(t')$ , $\hat{H}(t'')$ などと書くことにした.この式を展開すると次のようになる. それでも同じことだ.結局は右辺には $\hat{U}(t'')$ などというものが残るのである.それでも懲りずに,さらに代入を続けて行ったらどうなるだろうか. 規則性のある級数として表すことに成功したようだ.こうして右辺の $\hat{U}(t)$ を無限の彼方へ追いやることが出来るのである.無限の和が発散してしまわないかという点が気になったりするが,これがとりあえずの結論らしい.

時間順序積の例

今求めたばかりの結果をもっとエレガントに,シンプルに表現する方法がある.そのためには「時間順序積」あるいは「T 積」と呼ばれる一つのルールを導入するだけでいい.

それをここで紹介しておこうと予定していたのだが,ざっと調べたところ,「シンプルに表現できる」ということ以外には大した利点があるようには思えないのである.とりあえず先の方まで進んでみて,どうしても必要だということであればここに説明を追加しようと思う.将来のためにここに場所を確保しておこう,というわけだ.ちなみにどんな形に表現できるかというと, という感じである.これが (4) 式と等価なのだ.ここまで書いて説明をしないのはちょっと意地悪かな.しかし面倒な割りに得るものが少ないのである.

・・・.たった今,未来の自分から連絡があって,この部分はここで説明しておいた方がいいとのことなので,理由は分からないがやっておくことにしよう.

まず時間順序積のルールについて説明すると,(5) 式のように T[…] で囲まれた部分の中に時間の異なる複数の演算子が入っている場合には,時間の未来のものが一番左に,過去のものが右に来るように並べ替えをせよという決まりである.（とだけ書いて,その後のカッコを書かない場合もあるし, $\overrightarrow{T}$ のように書く場合もある.このあたりは教科書によって色々だ.）

とは言うものの,(5) 式を見る限りではそのルールをどこにどのように適用したらいいのか良く分からない.それで, T[…] の中身の指数関数を展開してみよう. ほら,どうだ.(4) 式とそっくりになっただろう.しかしわずかに違いがある.分かるだろうか？この式と (4) 式の各項が同じであることが証明できればいいわけだ.例えば,第 3 項どうしを取り出して比べてみよう. 左辺にはが入っているが,右辺にはない.さらに積分範囲も違っている.左辺はどちらの変数も 0 からまで積分しているが,右辺では片方の積分がまでである.

これはどういうことかと言えば,左辺のカッコの中では dt' と dt'' とが,お互いの大小関係にお構い無しに積分範囲を移動して計算が実行されるのである.一方,右辺では dt'' の移動範囲はまでであり, dt' の方がまで積分される.つまり, t'≧t'' という関係があるのである.

何が起こっているか把握しにくいかも知れないので,もう少し話しておこう.右辺では dt' が 0 からまで積分されるが,その変化のさなかに, dt'' の方は, dt' の現在ある場所までに積分範囲が制限されるのである.と t'' の平面を思い浮かべるといいかも知れない.

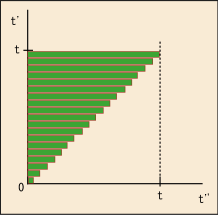
右辺の積分は,左辺の積分の半分の範囲でしか行われていないことになるわけだ.これだけの違いなら左辺を 2 で割っておけば済む.実際,で割っているからその点は解決しているはずだ.

しかしもう一つの問題は, $\hat{H}$ というのは時間が経過するごとに別の形の演算子に変わってゆくのだから, $\hat{H}(t')$ と $\hat{H}(t'')$ とは順序の入れ替えをするわけにはいかないという点だ.右辺では必ず $\hat{H}(t')$ が未来で $\hat{H}(t'')$ が過去という並びになっているが,左辺では積分計算の途中でと t'' の大小関係がひっくり返る場所があるために, $\hat{H}$ の過去未来の立場が入れ替わることがあるわけだ.時間順序積というのは,そのようなことを決して許さずに途中で順番を変えてでも計算を進めなさい,という指示なのである.

次の項以降も同じことである.(4) 式の第 4 項はと t'' と t''' の 3 つの変数で作られる立体領域のうちの三角錐領域での積分になるから,それは立方体領域の 1/6 のサイズになる.それで (5) 式の対応する項ではで割っているわけだ.かくして,(4) 式と (5) 式は同じ内容なのだということが説明できた.

そういう表現方法もあるのだな,くらいに覚えておいて貰えばいいと思う.

これで全てか

ハミルトニアンというのは系の全エネルギーを表している量だった.それが時間によって変化するというのは,外界とのやり取りがあってエネルギーが保存していないということを意味する.

つまり前回は全エネルギーが保存する場合を扱い,今回は全エネルギーが保存しない場合を扱ったことになる.すると,これであたかも全ての状況を言い尽くせたかのような気分になるわけだが,そう甘くはない.

ハミルトニアンが時間に依存する形でうまく表されるというのは特殊なケースなのである.しかし教科書に出てくる例といえばそういうものばかりだから,それ以外の状況があるなんて想像も付かないわけだ.当たり前のことだが,教科書というのは何とかして解けるような問題しか扱わないものである.

例えば,状態の変化に応じてハミルトニアンの形が変わるような仕組みになっていたらどうだろう.時間が直接は出てこないから今回の論法は当てはまらないだろう.量子力学でそのような具体例があるのか,また,その処方箋があるのかは私は良く知らないが,少なくとも古典力学の場合にはそれに似た分かりやすいケースが存在する.粒子がある領域に差し掛かったときだけ摩擦力が働くとか,壁からの反作用を受けるとか,だ.

念のため、まとめ

あらゆる状況に対応できるようになったと安心するわけにはいかないが,とりあえず理論上はハミルトニアンが時間依存する形で書かれている場合についても時間発展演算子 $\hat{U}$ を導くことができた.これを使って前回と同じような方法でハイゼンベルク描像を考えることが出来るだろう.前回の話で (2) 式のような演算子を使って説明していた部分を,全て $\hat{U}$ という記号に置き換えて繰り返してやればいいのである.とは言うものの,言うほど簡単に行かない部分もあるから,出来るだけ丁寧にやってみせよう.

ハミルトニアンが時間を含まない場合には,状態の変化は (2) 式のようなユニタリ変換を使って (3) 式のように表せばいいのだった.しかしハミルトニアンが時間を含む場合にはこのような単純な形では表せず,代わりに時間順序積を使った (5) 式のようなユニタリ変換を使って (3) 式のように表すことになる.いずれにしてもユニタリ変換であることには変わりない.(3) 式をもう一度ここに書いておこう. 先ほどまでは丁寧に $\hat{U}(t)$ と書いていたが,式変形が見にくくなるので $\hat{U}$ にしておいた. $\hat{U}$ が時間経過によって次々と変化する演算子であることは忘れないでいてほしい.さて,物理量の期待値を求めてみよう.この関係を当てはめることによって次のように計算を進めることが出来る. この式の中の $\hat{U}^{†}\hat{A}\hat{U}$ の部分をひとかたまりの演算子として見てやって, と定義してやれば, という形に書ける.この $\hat{A}(t)$ というのがハイゼンベルク流の演算子であり,時間によって変化する演算子である.それを時間によって変化しない固定した状態 $|ψ(t_{0})>}$ に作用させることで期待値を計算するというのが,ハイゼンベルク流のやり方である.ここまで,時間を含まないハミルトニアンについて考えた前回の話と全く同じ内容である.

次に,ハイゼンベルク方程式が問題なく得られるかどうかを確かめてみよう.(6) 式の両辺を時間で微分してみる. 右辺に出てくる $\hat{A}$ は時間によって変化しない演算子であり, $\hat{U}$ は時間によって変化する演算子であるからこうなるのである.しかしこの先をどう続けてよいのか分からないので一旦おあずけである.ここでシュレーディンガー方程式を持ってくる. ここで使われているハミルトニアンは,時間を含むハミルトニアンであるが変数を書くのは省略してある.これを次のように書き直そう. さて,(3') 式の両辺も微分してみよう. $|ψ(t_{0})>}$ は時間変化しない固定した状態なので,このように $\hat{U}$ だけを微分してやればいいのである.この (8) 式と (9) 式の左辺は同じなので,右辺どうしを等号で結んでやろう. よく見ると作用する相手も同じなので,演算子だけの関係式が作れそうだ. これを (7) 式に当てはめてやれば,先ほど止まっていた計算が再開できる！こうして無事にハイゼンベルク方程式が成り立つことも確認できた.変形の終盤で $\hat{H}(t)$ というものが出てきているが,これはハイゼンベルク流の演算子であることを意味している.ここでのハミルトニアンは元々時間を含んでいるという前提だが,そういう意味ではなく,時間経過によって演算子の形の方が変化するという意味合いで書いてある.この場合には二重の意味合いで時間変化しているわけである.