歴史
質量を持たないはずの光でさえ重力に引き寄せられて曲がる.これは一般相対論が予言した重要な現象の一つである.この現象がとても奇妙なことのように思えてしまうのは,ニュートン力学の考えに慣れてしまっているからであろう.
ニュートン力学では重力というものを,質量と質量の間に働く力だと解釈しているからだ.光は質量を持たないのだから引っ張られる理由が無いと考えてしまう.
実は光は引き寄せられて曲がるのではなくて,相変わらず真っ直ぐ進んでいるのである.空間が曲がっている為に,傍から見れば曲がったコースを進むように見えるだけなのだ.
ところが驚いたことに,相対論が発表される 100 年以上も昔から,光が重力によって曲がるという理論は存在していたのである.ええ!何だって!?いや,間違いじゃない.それは何と,ニュートン力学を使って計算されていたのだ.
おかしな話だと思う人もいるだろう.しかし,光に質量があるかないかなんて事は当時はまだ論じようがなかったし,重要な問題でもなかったのである.当時は電磁波という概念もなかった.光が波であるか粒子であるかさえ,まだ意見が対立していた時代の事だ.光を粒子として考えてやれば,光の質量が分らなくとも,その軌道を計算してやることは出来るのである.
地球の周りを運動する質点についてニュートン力学で計算する時,その軌道は質量には関係無い事が分かる.もし人工衛星が二つに割れたなら,その瞬間から二つのパーツは全く別々の軌道を辿ることになるだろうか?だとしたらおちおち宇宙遊泳などしていられない.質点の軌道を決めているのはその速度なのである.どんなに小さな質量のものであろうと,逆に大きな質量のものであろうと,初速と投射方向が同じならば,その後は同じ軌道を辿ることになる.
だから光に対して同じ理屈を適用してやるのは自然な考えではないか.秒速30万キロメートルで進む物体と同じだと見なして計算してやればいいだけだろう.ただしニュートン自身がこのようなことを考えたのではなかった.別の理論家たちによって,たびたびこのようなことが論じられていたのである.
このように理論はあったものの,昔はまだ観測精度が高くなかったので,この現象が起こるかどうかを確認する事のないまま,時代は過ぎて行った.
ニュートン力学による計算と一般相対論による計算とでは曲がり具合の数値にちょうど 2 倍の差が出る.相対論は,より強く曲がるだろうという予想を出した.これによってどちらの理論がより優秀であるかを比較してやる事ができるではないか.
このことについての歴史上初めての確認は,1919 年,エディントン卿の観測隊により,日食を利用して行われた.
太陽と同じ方向にある星というのは普段はまぶしくて見ることができない.昼には星は見えないものだ.しかしその星は別の季節ならば太陽とは違う方向にあるので,夜に見ることができて,その位置も良く分かっている.しかし,日食で太陽が月に覆われた時だけは,その星が昼間にも見えるのである.その時にその星が本来見えるべき位置と比べて,少しずれた別の場所に見えたとしたら,それは星からの光が太陽の重力で曲げられた事を意味する可能性があるわけだ.
しかしこの効果は実に微妙なものである.太陽の質量では空間はそれほど強く曲げられない.理論的には 1.75 秒角だというから,そのずれは太陽の視直径の約 1100 分の 1 程度でしかない.本当に難しい観測だ.
その結果がどうだったかというと,確かに光は曲げられて地球に届く事が確認されたのである.いや,この辺りの歴史はもう少しだけ正確に話しておいた方がいいだろう.
実はこの年より前,まだ一般相対論が発表される何年か前に予備的な観測は行われていたのである.アインシュタインは一般相対論を 1915 年の発表までひた隠しにしていたわけではなくて,そのアイデアの途中経過をたびたび論文として発表していた.物理の研究というのは大抵そういうものだ.アインシュタインはまだ正しい理論値を導き出すことは出来ていなかったが,等価原理が正しければ光は曲がるはずだと考えていたのだった.それを確かめるべく,観測実験が計画された.信頼の置けそうな理論があり,その真実性を確認できる可能性がわずかでもあれば,誰かが苦労してでもそれを実行してくれるものだ.そして予備実験ではまだ精度は十分でなかったものの,予想した現象があること自体は確認されたのでアインシュタインは大いに喜んだと言う.それで彼は勇気を得て研究を続けたのであった.
では 1919 年の観測結果はどうだったかと言うと,微妙なものだった.確かにその時,ニュートン力学による予想よりも相対論の予想する値に近いことがはっきり分かる結果が出た.なぜなら,相対論の理論値よりもさらに少しばかり大きめの値が観測されたからだ.ではどこが微妙かと言うと,理論値は見積もられた誤差の範囲内に入らなかったのである.この実験は現在の視点から見直すと,見過ごされ検討されていない誤差が幾つかあることが指摘されている.当時としてはそれほど難しい測定なのであった.
最近では可視光以外の光や電波領域までも使って非常に精度の良い観測ができるようになってきた.太陽を挟んだ宇宙探査機との通信など,色々な種類の実験が行われており,十分な精度でその理論の値との一致が確認されているのである.その誤差は実験の種類にも依るが 1 % から 0.001 % 程度にもなるらしい.観測技術も驚くべき進歩をしたものだ.そして,その精度をもってしても未だに理論に修正の必要がないという点も大したものだ.
相対論が間違っていると信じる人は別にそれでも結構だが,その主張を認めてもらうためには,相対論とまるでそっくりな結果を導き出す別理論を構築する必要があるだろう.そうでなければその主張はただのお遊びだ.
以下では今の話に出てきた理論値がそう簡単なお遊び程度の考えで導けるようなものではないことを示す事にしよう.しかしなるべく分かり易く行きたい.
測地線の式を書き出す
まずは,曲がった時空の中での真っ直ぐな線というのがどういうものかを調べよう.これは測地線の方程式を使えばいいのだった.
これにはクリストッフェル記号が使われているが,ここには前回求めたシュバルツシルト解の結果を当てはめてやればいい.前回は計算過程のものを書いたので,最終的な解を当てはめた形をここに書き直しておこう.
これらを代入した結果,次のような 4 つの方程式を得ることになる.
これを解くことで 4 次元曲面上に引かれた直線の式を得ることになるのだが,
という媒介変数が使われているのが気になる人もあるだろう.言っておくが,これには特に物理的な意味は無い.例えば,2 次元平面上の円の方程式を媒介変数表示をしてやると次のような二つの式で表せるが,これに似ていると言える.
ここで
,
には座標の意味があったとしても,
には特に意味が無いのだった.
の代わりに
や
を使うようにしても円の形は変わらない.しかし場合によっては
に時間の意味を持たせるために調整してやることも出来る.
もこれと同じであって,最終的には消去してやってもいいし,何か目的があるならば物理的意味を持つように調整して残してやってもいい.今回は消去してやるつもりでいる.
それにしてもこの 4 つの式は・・・,ああ,何ということだ.もっと単純な式が出てくるのを期待していたのに・・・見ているだけで解く気が失せてしまいそうだ.何とかいい方法を考えてみよう.まず,であると固定してみることにする.そうすれば
を含んだ幾つかの項がさっぱりするだろう.
しかしこんな人為的な仮定を持ち込んでいいのだろうかと少し不安になる.この仮定はこれ以後,平面のみで考えることを意味している.太陽を含むある面内を通ってきた光は,太陽の重力によってその面以外の方向へ逸らされることは無いと考えても大丈夫だろうか.
その辺りは心配ないようだ.なぜなら (3) 式はこの仮定条件を満たして完全に消えてしまうのである.今は球座標を使っているのでたまたま平面が特別扱いされているだけであり,本当は太陽を含むどの面でも同じ内容のことが許されるのである.
変更のある式だけ,もう一度書いておこう.
これで考えるべき式は (1) (2') (4') の 3 つに減った.少しはすっきりしたが期待したほどには簡単にならなかったか・・・.それでも (1) 式と (4') 式は両方とも一定の手続きで解くことが出来る形になっている.そのやり方は別ページで説明することにして,結果だけを書くと次のようになる.
ここで新しく出てきた
や
は積分定数だ.これらの式を残る (2') 式に代入すると,次のようになる.
さあ,
だけの式にまとまって,解き易くなってきたではないか.
光速の条件を入れる
ところで測地線の式というのは,これらの方程式を使ってただ一本だけが求まるのではない.4 次元曲面の上には,色んな向きに線が引けるわけだ.ある線は今採用している座標系の空間座標に対して静止している物体を表しており,それは時間軸方向だけを目指して進む軌跡を描くだろう.またそれ以外の線は移動する物体の時空グラフ上の軌跡を表しているが,それも速さや進行方向によって色々な線があるだろう.そして今知りたいと思っているのは,光の軌跡がどうなるかである.そこに限定するために,もう少し条件を絞ることが必要だ.今こそ,を使うのである.特殊相対論での
の定義式を思い出してみるといい.これが 0 であることは光速であることを表しているのだった.今はシュバルツシルト解を使っており,
は次のような式となる.
この式が意味するのは,一般相対論においては光速は観測者の立場によって,場所場所で変わるものであり,もはや
で一定だとは限らないということである.しかしその光が存在する現場に立って見るとやはり光速は
なのである.今,さらっと大事なことを言ったぞ.今回の記事は単なる応用計算の解説ではなくて,補足説明を兼ねているのだ.心に留めておくように.
さて,上に書いた式をで割ってやって,今は
を固定しているので
であることなどを入れて,
と置いてやると,
という式になるであろう.ここで出てきた
,
の部分に先ほど解いた式を代入すれば,次のようになる.
これは (5) 式の第 2 項にそのまま当てはまる形ではないか!代入して整理してやろう.
ずいぶん簡単になってきた.それでも解が一つに絞られたわけではないことに注意しよう.今は光の速さの条件を入れただけであり,光がどの方向へ進むかを特定したわけではないから,まだ無数の軌跡が解として許されているのである.
距離と角度の関係式を得る
さて,このまま,
,
の 3 つの式の形をそれぞれに得ようとすることは効率的だろうか.我々の目的は一体何だったかを思い出してもらいたい.光の軌道が求まればいいのだから,時間
はそれほど重要ではない.位置座標
,
と媒介変数
との関係も必要というわけではない.最終的にただ
と
の関係式が得られればそれでいいのである.
例えば,と
の関係として
という関係が成り立っていたとしよう.何だか面倒臭そうだが,これは何のことは無い,太陽の中心から距離
のところをかすめて真っ直ぐに通り過ぎる直線の式である.図を描くと分かりやすいだろう.
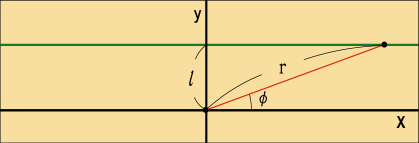
太陽が無くて時空が曲がっていなければこんな軌道になるはずであるし,太陽があってもそれほど強くは曲がらないはずなので,きっとこれに良く似た関係式が得られるだろうと予想される.目標としてはこんな感じの関係式が欲しいわけだ.ここでは関数という形を考えてみたが,代わりにその逆数を取ったものを新たに導入した方が,
関数が分母に来なくて楽になりそうだ.
まぁ,これは試行錯誤の結果,この先こうした方が楽だと知っているから導入するのである.こうした方が絶対に効率的だといきなり気付く人は天才か他で経験を積んできたような人だけなので安心して欲しい.次に
の微分を
の微分に置き換えるべく計算してみる.
こうして
から
への置き換えのルールは分かったが,本当は,
を
の関数として考えたいのである.ここを置き換えるルールも知りたい.
以上の結果を代入すれば,(6) 式に含まれる
を全て
を使った形に変形することが出来るだろう.その結果が次の式だ.
これが,今回の目的を達成する為に,たった一つにまとめ上げられた微分方程式である.どうだい,このすっきりした美しさ.さっそく解いてみたいだろう.これが,そう簡単ではないんだな.
近似解法
この (7) 式の左辺第 2 項と右辺との比はだが,まずそれがどの程度か考えてみるといい.
は太陽のシュバルツシルト半径を表しており,それは 3 km ほどだ.一方,光は少なくとも太陽の半径(約 70 万 km)より遠いところを通るのである.左辺と比べて右辺は無きに等しいことが分かるだろう.だからまず右辺を 0 と置いて解を求めてやり,解の見当を付ける.まぁ,これはすぐに解けるのだ.
が余分に付いてきている事を除けば,先ほど例として出した,太陽が無い場合の直線の式である.
が入っていても直線の式である事は変わらず,ただ向きが変わるだけである.
とすれば
軸と平行に通り過ぎる軌跡を表すことになるので,今後はこれを基準に考える事にすれば楽だろう.右辺のシュバルツシルト半径
が重力の存在を象徴しているのだから,右辺を取り去った場合の解がこのようになるのはまぁ当然だと言える.
ここにもし右辺が付け加わったならば,解はこれに対してごく僅かだけ異なったものとなるに違いない.それを次のように表現してやる.
これを丸ごと,右辺を省かない元の方程式に代入してやるのだ.
右辺の第 2 項以下は第 1 項に比べて十分小さいと考えられるので無視してしまおう.
こうして結局,光線の軌道は,重力が弱い場合の近似ではあるが,
だと言えるわけだ.ほぼ直線であるが,そこからわずかに逸れることになる.どれくらい逸れるかについては
になるところで
が幾つになるかを調べれば良い.つまり
と置いてやればいいのだ.そうすると
についての二次方程式となるので,解の公式に当てはめればいい.
関数の絶対値は 1 を越えるはずがないので,負の解のみを採用してやるべきだ.
角度が非常に小さい時は
という近似が成り立つ.よって
軸の右と左の両方でそれぞれ
ラジアンだけ
軸から逸れていることが分かる.
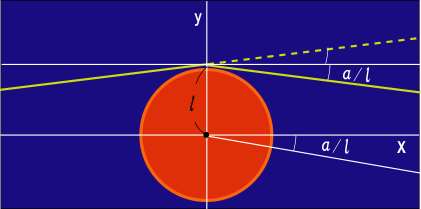
宇宙の彼方から太陽の縁を目掛けて飛んできた光は,合計してラジアンずれた方向へ飛び去るという計算だ.
に太陽のシュバルツシルト半径,
に太陽の半径を入れて計算してみるといい.
こうして冒頭で話した通りの数値が得られた.











すごいレベルで行われているんだね。