相対性理論：重力波の偏極モード

確認

重力波が光速で伝わる横波であり,進行方向に垂直な 2 成分があるというところまでは前回導いた.平坦な時空を重力波が伝わるときの時空の計量 $g_{ij}$ は次のように表されるのだった. この $h_{ij}$ が重力波を表しており,うまく座標を選んだ時には独立な成分は $h_{11}(=-h_{22})$ と $h_{12}(=h_{21})$ のみで,残りの成分は 0 である.要するに次のような具合である. このやの部分が波のように変化するのであるから,ある固定した場所での計量の変化を表現しようと思ったら次のような簡単な波の式を代入しておくだけでいい. δ_a と δ_b は二つの成分の位相の違いを表すために入れている.二つの成分は独立であって,必ずしも同じタイミングで揺れる必要はないからである.波長もそれぞれで違っていてもいいのだが,合わせておくと後で面白いことができるので共通にしておいた.

これを見ると,時間成分や波の進行方向成分については何も変化しないことが分かる.進行方向に対して垂直な面内での二点間の距離にだけ変化が生じるのである.その面内だけを考えることができればいいから,以後は他の成分は省略して 2 次元空間での計量を考えることにしよう. もも 0 であれば,この 2 次元はただの平面だ.しかしやが変化するときに起こる変化をどのように表したら良いだろう？

平面だったものが歪むようなイメージを描いてもいいかも知れないが,そのためには立体図を使って表すことになるのだろう.しかしそれは現実の方向に歪んでいるのではなく,「どこか不思議な方向」へ向かって歪んでいるのである.そんな図を描いたとしても現実離れしているし,本当にその形に曲がっているとも言えず,参考図でしかない.

苦労してそういう偽物の図を描かなくても,もっと楽して表せる方法はないものだろうか.

歪みをイメージする方法

2 次元の計量が単位行列である場合には微小な 2 点間の距離は次のように表せる. もしその計量が変化して $g_{ij}$ になったなら,その距離は次のようになるのである. この距離を実感してもらうために同じ値を平面図の上で表そうと思ったら,とに何らかの座標変換をして次の形式で表せるようにしてやればいいのである. これって,線形代数に出てきた行列の対角化,その応用である「2 次形式の主軸変換」そのものではなかろうか.そう思って試してみたが,根号だらけになって面倒くさくなり,断念した.

しかしやりたい事を行列の式で表すと次のようなことなのである. この条件を満たすようなとを見付けるのはそれほど難しくなさそうではないか.なぜそんなに複雑になってしまうのか？

この問題を解く為には ( dx, dy) と ( dx', dy') との関係を見付けることも必要だな.いや,むしろそれこそが目的なのだった.仮に次のように表しておこう. また,(2) 式の両辺の転置を取れば,次のようになる. (1) 式の右辺に (2) 式と (3) 式を代入すればとなるので (1) 式の左辺と比較できる形になる.結果は次の通りだ. うーん,これでは未知数に対して条件が圧倒的に足りてない.

そうだ,目的を考えれば X=Y=1 としてしまってもいいのではないか.そうすると ds^2 = dx'^2 + dy'^2 となるが,このが微小距離を直接に表すことになる.むしろこの方が好都合！主軸変換にこだわる必要はないのだ. しかしこれでもまだ条件が足りてない.一体どうすればいいというのか.

おそらく,この条件を満たす解は複数ある.いや,主軸変換の方法に従って忠実にやればそうでもないのかも知れないが,今はもう,少し違ったことを考えている.複数あるかも知れない可能性の中から,物理的な条件に合うものを探し出すことにしよう.

例えば,もしもも 0 だったならば,このような変換は必要ないので (s,t,u,v) の行列は単位行列になるはずだ.すなわち s=v=1 かつ t=u=0 である.やが少しだけ顔を出せばの値はそこからほんの少しだけズレるのだ.だから次のように置くことにしよう. つまり,変数 (s',t,u,v') はいずれもごくごく微小量であると考える.こうすれば,先ほどの条件式はとなる.式を簡単に出来そうな予感！もう近似解でいいや.微小量どうしの掛け算はごく小さくて無視できるものだとして省いてしまうことにしよう. これではまだとが定まらないが,が増えることによる効果は, dx' と dy' のどちらも同じように引き受けると考えよう.ここまでの結果を集めるとこういうことだ. おそらく,最初に考えた主軸変換の方法に頼ると根号ばかりの複雑な式が出てきて,その近似を考えることで無理やり根号を整理するとこれと同じ結果が得られるのではなかろうか.そちらは確かめる気にはなれない.

とにかくこれで目的が果たせそうだ. ( dx, dy) を使って表されている 2 点間の距離が,重力波が来た時にどのように伸び縮みするのかを ( dx', dy') を使うことで表せるのである.

図示してみる

平面上の原点を中心にした円を考え,その上に幾つかの点を配置しよう.

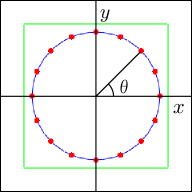
重力波が来た時に,原点からそれらの点までの距離がどう変化するのかを図示してみる.(4) 式の ( dx, dy) に (cosθ,sinθ) を代入すればいい. この式を使ってが変化するときの様子をアニメーションで表してみよう.分かりやすいようにだけが変化する時とだけが変化する時を分けて表すことにする. B=0 でやってみると次のようになる.

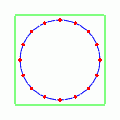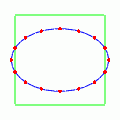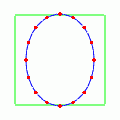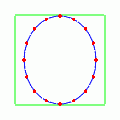
A>0 で横に伸び, A<0 では縦に伸びる動きを見せる.ここでは分かりやすいように変化をかなり大袈裟に表してあるが,実際はほとんど分からないくらいの歪みである.縦に伸びる動きと横に伸びる動きをもっと大袈裟に表してその残像を見ると,まるで「＋」記号のように見えることだろう.それでこの動きを「プラス偏極モード」と呼ぶ.

次は A=0 でやってみよう.

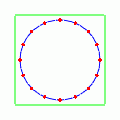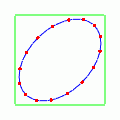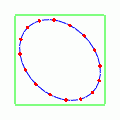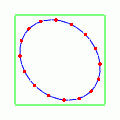
今度は先ほどの動きを 45°傾けたような振る舞いをする. B>0 で右上に伸び, B<0 で左上に伸びる.残像がまるで「×」記号のように見えるので,この動きを「クロス偏極モード」と呼ぶ.

これら二つのモードは理論の上で区別されているだけであり,物理的には何の違いもない.見る角度が違うだけのことである.実際に重力波が観測されたとしても,どちらであるかを決めるような手がかりはない.

では次に,二つのモードを重ねたらどうなるだろうか？ただ重ねただけではあまり面白いことにはならない.45°のさらに半分だけ傾いただけの状態の,ここまでに見たのと同じような動きが繰り返されるだけである.

しかし二つのモードの位相を π/2 だけずらして重ねてやると面白いことが起こる.一方を sin 波に,他方を cos 波にして重ねるようなものである.

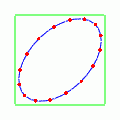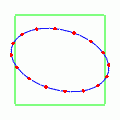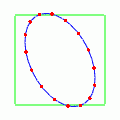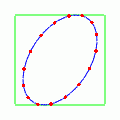
この場合,真円に戻る瞬間はなくなって,楕円がぐるぐると回転するような様子を見せる.遠くから見ると楕円が回転しているだけで何も面白く無いのだが,楕円上の点の動きを見ていると,こねられているようで酔いそうになる.重ね方の位相を逆にして一方を cos 波に,他方を sin 波にしてやると,逆回りさせることも出来る.

電磁波でも同じようなことが出来たのを思い出すだろう.方向に進む電磁波の電場成分は,方向に振動させてやることも方向に振動させてやることもできるが,二つの電場成分の位相をうまく π/2 ずらして重ねてやると進行方向に対して右回りに回転する電場や左回りに回転する電場が作り出せる.これを「円偏光」または「円偏波」と呼ぶのであった.重力波についてもこのような波を「円偏波」とか「円偏極した重力波」とか呼ぶ.

さて,では位相を π/2 ずらすのではなく,少しだけずらしてやるとどんな感じになるのだろうか？次の動きはプラス偏極モードの位相だけを π/4 だけ進ませてやったものである.

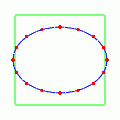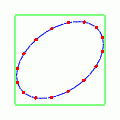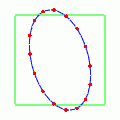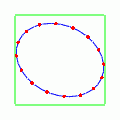
楕円が回転しているようでもあり,同時に楕円の形が伸びたり戻ったりするような中途半端な動きである.完全な円に戻る瞬間はないようだ.

重力子のスピン

先ほど,電磁波の円偏波との類似点について触れた.電磁波に右回りと左回りの自由度があることが,素粒子論では光子のスピンに対応しているのである.光子のスピンは 1 である.

重力を伝える素粒子というものは未だに発見されてはいないが,もしあるとすれば重力波を量子化する形で導かれるものであるはずである.それは「重力子」とか「グラビトン」とか呼ばれている.それはあるかも知れないし,ないかも知れない.もしあるのならそのスピンは 2 であろうと言われている.それに関わる話をしておこう.

前回の記事で,電磁波と重力波の方程式の違いはベクトルかテンソルかの違いだけだという話をした.今こそ,その違いがどこに現れるのかを示そう.軸を中心にした面内での回転を考える.自分がだけ回転して新しい視点で重力波を観察する時,新座標と旧座標の変換は次のように表せる. この時, $h^{ij}$ はテンソルであるから次のような変換規則に従う. ここで $h_{ij}$ ではなく $h^{ij}$ を使っているのは,その方が (5) 式を当てはめやすいからである.計算が終わったら元に戻すことにしよう. $h^{ij}$ は微小量であるという仮定があるから $η_{ij}$ で変換してやるだけで $h_{ij}$ に戻るので,実質は同じものであると考えれば済む.しかし先走った考えでデタラメな計算を見せるわけにも行かないから今は規則に従っておこう.本来このような 4 × 4 成分の 2 階テンソルの変換は 16 個の項が出現する複雑なものだが,今は面だけでの変換であるからほとんどの項は 0 になり,次のような項だけが残る. この両辺に $η_{ij}$ を掛けてやれば全て $h_{ij}$ にすることができる.こういう作業が,論理が直接的でなくなる気がして嫌なら,初めから (x',y') と (x,y) の関係を逆にしておいて 2 階共変テンソルのルールで変形してやれば良かったのである.

この結果に,冒頭での次のような仮定を代入してみよう. 2 倍角の公式が使えて,次のようになる. これはつまり,こういうことではなかろうか. $h_{21}$ や $h_{22}$ について計算してみてもこれと同じ結果が導かれ,矛盾しない.この結果は (5) 式の回転変換にとても似ている.図形的に見ればとの値をそれぞれ横軸,縦軸に取ったものを回転させるようなイメージだ.これは二つのモードの波を π/2 だけずらして重ね合わせた波が位相のズレを保ったまま振幅を変化させる様子を表しているようである.

それにしても奇妙なのはの部分である.視点をだけ回転しただけなのに,波の位相がその倍のも変化するというのだ.視点を 1 周させるとその間に何かが 2 回転しているということだろう.半周すれば元に戻るというのである.確かに,先ほどの円偏極のアニメーションを見ると,半周回った時点で最初と同じ形に戻る.楕円は 180°対称だからだ.しかしそれは少し違う気がする.30°視点を変えると 60°変わるような何かがあるはずなのだ.しかし当たり前の事だが,アニメーションを 30°傾けて観察したところで楕円は 30°傾くだけである.

ところが良く見ると,このアニメーションの中に,倍の回転をするものが現れているのである.楕円の上にある各点の動きに注目してみて欲しい.楕円が一周する間に,その場で 2 回転しているではないか！

しかしこれではまだ状況が正しく表せていないし,右回りと左回りの違いも入っていないのでもう少し続けよう.重力波の円偏波は複素形式を使って,例えば次のように表せる. 複素形式では虚数を掛けることで π/2 だけ位相をずらしたことにできるので,こんなにシンプルに表せるわけだ.しかし実際に意味を持つのはこの実数部分だけである.は回転に二つの方向があることを表している.

この波をだけ回転した視点で観察するとどうなるかというのは (6) 式に当てはめればいいわけだが,にはが代入され虚数軸を表していることになる.つまり (6) 式は複素平面での回転を表しているのと同じであると解釈できて $e^{2iθ}$ を掛けたのと同じだとみなせる.またに -ib を代入した場合には複素平面の上下がひっくり返った状況での回転と同じであるから $e^{-2iθ}$ を掛けたのと同じである.これらをまとめると次のように書けることになる. 量子力学を学ぶと出てくることだが,電子のスピノル波は座標の回転に対して位相が $e^{iθ/2}$ だけ変化する.これは視点を 2 回転させることでようやく位相が元に戻るという不思議な状況であるが,電子のスピンが 1/2 であることに関連している.また電磁波は座標の回転に合わせて位相が $e^{iθ}$ だけ変化する.これは特に不思議でもないごく当たり前に思える振る舞いである.そしてこの対称性から光子のスピンが 1 であることが出てくる.重力波の場合,もしこれに関連する粒子があるとすればスピンが 2 になるのは想像が付くだろう.しかしずっと先の不確かなことにまで踏み込んで説明し過ぎた感じもある.