相対性理論：事象の地平線

ブラックホール

地球の場合のシュバルツシルト半径を計算するとわずか 9 mm 程度であるが,別に地球を掘っていっても中心に特別な領域が存在するわけではない.シュバルツシルト解は物質が存在しない領域に限定して解いたものなので,物質が詰まった部分には適用できないのである.

しかし質量の全てがこのシュバルツシルト半径の内側に凝縮してしまった場合には,当然このシュバルツシルト半径のところには物質がないわけで,この解を当てはめても良いことになる.しかしそこは不思議な場所で,その地点を傍から見れば時間が止まったかのように観察され,そこでは光さえも止まってしまうのだった.

また,この半径より内側から発せられた光は外側へ出てくることがない.もちろん物質も出てこれない.これは後でちゃんと確かめることにしよう.とにかくこんな具合であるから,シュバルツシルト半径の内側の様子は全く知ることが出来ないのである.

しかし前回も見たように,この点は数学的な特異点ではない.その場に行ってみれば光速は相変わらずであるし,時間も普通に流れている.少々詩的な表現をすれば,外部の時空の視界の範囲では,その続きとして起こる事件 (event) を見ることが出来ないだけなのである.

そのような状況が,まるで地平線の向こうの景色が見えないことに似ているというので,このような地点のことを「事象の地平線」と呼ぶようになったのである.地点と言っても点ではないし,地平線と言っても線でもない.それは天体を取り囲むように存在する「面」として存在するのである.

それで以前はこれを「事象の地平面」という洒落た呼び方をしたものだが,もともとは英語の「event horizon」を訳したものであり,英語圏にはそのような地平線だか地平面だかの言葉の区別はない.日本独自のこだわりに過ぎなかったというわけだ.最近は素直に「事象の地平線」と訳することの方が増えたようだ.

事象の地平線に囲まれた天体のことを「ブラックホール」と呼ぶ.これは 1967 年にジョン・ホイーラーにより名付けられたそうだ.割と最近のことである.それ以前は「コラプサー（潰れた星）」と呼ばれていたのである.

このブラックホールという名前のインパクト故に,研究者のみならず一般の人々の興味や関心が寄せられることになった.なるほど,私の子供の頃に SF ブームがあり,色んなアニメや映画,不思議本などに頻繁にブラックホールが登場していたが,当時の最新の話題だったというわけだ.

シュバルツシルト半径は現実の特異点ではない

ではいよいよ,シュバルツシルト半径の内側へと降りてゆくことを考えよう.シュバルツシルト解は次のように表されるのであった. この中でで表されているのがシュバルツシルト半径である. この解を見ると,シュバルツシルト半径に近付くにつれて第 1 項は 0 に限りなく近付くし,第 2 項は無限大に発散してしまう.そこで何かとんでもないことが起きているような,まるで時空がそこで壊れてしまっているような印象を受ける.

しかし似たようなことは以前の話にも出てきたのだった.以前の記事で「一様加速系のことをリンドラー座標を使って考えた」ことがあったのを思い出してみよう.加速度系にいる人にとっては特別に凄まじい性質を持つように見える場所があり,「ブラックウォール」と呼んだのだった.しかしそこは傍から見れば何でもない普通の空間なのである.

(1) 式が r=a に特異点を持つように見えるのは座標の選択がうまく合っていないせいであって,その地点を通過する人にとっては現実にひどいことが起きているというわけではない.そこに留まろうとする人にとってはとんでもない場所に見えるだろうが.

そこが特異点ではないということについては前回の話でも十分だろう.(1) 式を極座標からデカルト座標に書き直すことをすると,シュバルツシルト半径での特異点らしきものは消えてしまうのをすでに見たのだった.

ブラックホールまでの距離

わざわざ別の座標を導入しなくても,ある程度までなら (1) 式だけでもシュバルツシルト半径付近での状況を考える事ができる.

(1) 式で使っている (w,r,θ,φ) という座標は重力源から十分に遠く離れた地点の,平坦な時空での時間と空間を基準にしたものであった.(1) 式の第 1 項が r→a の時に 0 に近付くのは,幾ら外界で時間が経過しようとも,シュバルツシルト半径の付近の「現場」にいる人にとってはほとんど時間の経過を意識していないことを意味している.が幾ら大きくても,にはほとんど影響しないということだからだ.

同様に,(1) 式の第 2 項が無限大に近付くのは,現場付近では,外界から判断するよりも重力の中心へ向かう距離が間延びしていることを意味している.

こういう話を聞くと,無間地獄を思い浮かべてしまう.ブラックホールに落ちて行く人は長い長い距離を永遠に渡って落ち続けるというのだろうか.それは都合のいい部分だけを拾って考え過ぎというものだろう.永遠の時間を感じるのは外界にいる人の方だし,思ったよりも長い距離だと感じるのは落ちている本人だけである.

それに距離が無限に間延びすると言っても,それはシュバルツシルト半径ちょうどの地点だけでのことである.距離が本当に無限大になっているとは限らない.例えば,無限大に発散するような関数を,無限大になる地点まで定積分した場合,結果が無限大になる場合もあれば,有限の値に収まる場合もあるではないか.下の図はその典型例だ.

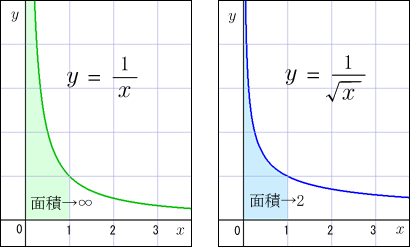
これと似たようなことになっているかも知れないではないか.しかしこの件については前々回の話で解決済みなのだった.半径 r_t の地点から r_s の地点まで降下した時の実際の距離を次のように計算したのを今思い出した. ここで r_s としてシュバルツシルト半径であるを代入したとしても有限の値であることが分かる.しかし残念ながら,この式ではシュバルツシルト半径より内部へ降りて行った時の距離が計算できない.値が虚数になるからである.

これは何を意味するのだろうか.シュバルツシルト半径を越えて奥へ入って行った人が実際にどれだけの距離を旅することになるのか,計算できないということだろうか.

この計算の意味をもう一度思い出す必要がある.これは「2 点の位置を,無限遠にいる人の肩を持つように作られた座標で測った場合の読みの値」と「実際に棒などを降ろして測った距離」の違いを求めたものである.シュバルツシルト半径までの距離が有限であることをこの式によって確認することはできるが,飽くまでも外側に静止している人の視点でしかない.

シュバルツシルト半径の内側にまで入ると (1) 式の第 2 項は負になってしまって,外部の人にとっては通常の距離としての解釈はできなくなる可能性がある.それに,これから詳しく説明して行くことになるが,シュバルツシルト半径の内側にまで棒を降ろして距離を測ることなど外部の人にとっては不可能なのである.そこは決して元の世界には戻れない境界線なのだから・・・.

さっきから,今までの説明の再確認や総まとめのようになって,なかなか話が先へ進まないな.しかし,じっくり解決して行こう.

落ちる人の視点

シュバルツシルト半径付近では光でさえ速度が 0 になり,まるでその場に凍りついたかのように解釈されるという話もすでに前回計算して求めたのだった.うーん,すでに何もかもやってしまった感じだなぁ.

とにかく,光でさえシュバルツシルト半径の手前で止まるのであれば他の一切のものはそれよりずっと動きが遅いに違いない.こんな状況で一体誰がシュバルツシルト半径を越えて内部へ入って行けるというのだろうか.シュバルツシルト半径に向かって落ちて行く本人にとって,シュバルツシルト半径近くでの体験はどんなものなのだろうか.

光の軌跡は ds=0 を満たすのだったが,物質の運動の場合はそうではない.代わりに ds^2 =- dτ^2 という関係を (1) 式に代入して考えよう.こうした場合,固有時は重力に任せて落ちてゆく本人の感じる時間に一致しているのだった.

話を簡単にするために,天体の中心に向かって一直線に落ちてゆくという設定で考えることにする.角度の変化はないのでもも 0 だということだ.ここまでの話を (1) 式に適用すると次のようになる. うーん,何だこれは？どう考えたらいいか分からない関係式ができただけだな・・・.まぁ,しばらく置いておこう.

他に何かやり残したことはないだろうか？(1) 式の形のシュバルツシルト解から引き出せる情報はこれくらいだろうか？ああ,そうだ！まだ測地線を試していない！

測地線についてまたややこしい計算をするのは嫌なので,以前に計算したものを拾ってくることにしよう.シュバルツシルト解を使って最初に測地線を計算したのは「光の湾曲」という記事である.そこの (1) ～ (4) 式が使えそうだ.それらに dθ = dφ = 0 を入れるともっとずっと簡単になるが,特に (3) 式と (4) 式は完全に消えてしまう.残るのは次の二つである. 元の式ではパラメータとしてを使っていたが,ここではに書き換えてある.これらの式もどう解釈したらいいかよく分からない形をしているのだが,(4) 式をじっくり見ていると (2) 式と良く似ている部分があり,組み合わせれば何か得られるような気がする.実際,項がうまく打ち消し合ってこんなに単純な式になってくれるのである！これは固有時が,運動している本人にとってのと同じだということを考えれば, という式と同じだということになる.これは質量の天体に引かれて落下する物体の運動方程式そのものだ.通常のニュートン力学と同じである.つまり,落下していく本人にとっては,普通の天体に落下していくのと全く変わらない感覚で,有限の時間でシュバルツシルト半径より内側深くまで到達することになることを意味しているわけだ.何も障害物がなければ有限の時間で r=0 まで到達するだろう.

では残った (3) 式は何を意味しているのだろうか.この形の微分方程式を解くことは先ほど引用した「光の湾曲」という記事の補足記事の中でやっている.結果はこうだった. は任意の定数である.物体がブラックホールから無限に離れた場所で静止している状態では座表時と固有時が一致しているので, r→∞ にて左辺が 1 になるように調整しておけばいいだろう.そうすれば b=1 になって考えるのが楽になるということだ.そのように仮定してみたところで,天体に落下していく物体の運動を表すのに差し支えないだろう. 物体がシュバルツシルト半径に近付くほどに dw/dτ が大きくなるわけで,これが意味するのは,落下する人にとっての一瞬が,外側にいる人にとっての永遠に等しくなってゆくということだ.そしてシュバルツシルト半径より内部に入ると,マイナスになり,わけがわからなくなる.時間の逆流でも起きるというのか？

先ほど放置した (2) 式にこれの左辺と同じものがあるので,ちょうどいい,試しにそこに代入してやろう. 何か新しい式を得たように思うかも知れないが,実はこれは (5) 式と同じ内容を別の表現で見ているだけなのである.(6) 式の両辺をで微分してみるといい.で微分するのではないよ. r(τ) だと考えてで微分するのである. ほら,(5) 式と同じだ.しかし完全に同じというわけではない.(5) 式は加速度についての式だったが (6) 式は速度についての式であり,物体が無限遠の地点にあるときに速度が 0 だという初期条件を入れてある式だからだ.実は (6) 式はとの関係を導くには都合のいい形をしているのである.との字体が似ていて紛らわしいので τ=ct を使って (6) 式をで書き直そう. 右辺にプラマイの記号が付いているが,今は時間の経過と共にが減少することがブラックホールの中心に近付くことなのだから,右辺が負になる方を選んで変形を続けることにする.これは変数分離型の微分方程式であるから次のようにして解ける. r=0 にたどり着く時刻を $t_{0}$ とすれば, $C = c√a t_{0}$ だから,次のようになる. 普通は $t_{0}$ を起点として考えることが多いが,ここでは r=0 にたどり着くのは未来のことだから $t<t_{0}$ であることに注意しよう.両辺ともに正であり,式の符号も問題ない.ブラックホールに落ちる人は有限の時間で r=0 までたどり着けることが確かに分かる.まぁ,わざわざここまでやらなくても (5) 式を見れば十分に分かることだけれど,念のためやってみた.

光が出てこれない

ブラックホールはなぜブラックなのか.それはその中から一切の光が出てこれないからだ.だから黒く見える.光でさえ出てこれないなら,もう何も出てこれない.内部から外部に通信する手段はなく,一方通行だということである.シュバルツシルト半径より内側のことは一切,知ることはできない.

そのことはどんな計算で導くことが出来るだろうか.もう試せることはみんなやってしまったような気がするのだが・・・.

測地線の方程式を使って光の軌跡を求めようとしてみたが,ごちゃごちゃした結果が出るだけで実りがなかった.次のようなことをしてみたわけだ.まず (3) 式と (4) 式に使われているを単なるパラメータとして見るためにとでも書き換える.光の軌跡の場合には固有時は意味をなさないので,惑わされないようにしたわけだ.そして (1) 式に ds^2 =0 を代入したものをヒントに変形を進めて行くのである.

しかしこの変形の目標は何だろうか.今はもも変化しないものとして考慮の外にあるので,最終的な目標はただを消去してとの関係を求めることにある.ところがそこへうまく辿りつけないのだ.

いや,との関係を知りたいのなら,こんなややこしいことをする必要はない.(1) 式で ds^2 =0 と置くだけですぐに求めることが出来るではないか.もちろん今の設定では dθ= dφ=0 であるから次のようになる. そう言えば,これと同じことは前回でもすぐに試してみたのだった.しかしこれを解いてみることはまだしていなかったではないか！早速試してみよう.

今はシュバルツシルト半径より内側でのことを考えようとしているのだから r<a である.すると (7) 式の右辺のカッコの中は負である.今は光が外側に向かって飛び出してこれるかどうかを知りたいので,が増加するような式を導きたいわけだ.すると右辺にあるプラスマイナスの部分はマイナスを選んで,右辺の全体が正になるようにする必要がある. これも先ほど解いたのと同じ変数分離型の微分方程式だから,同じ要領で解けるだろう. ここで,ブラックホールの外側にいる人にとっての時刻 w=0 における光の位置を $r_{0}$ だとすると,定数は次のように決められる. もちろん $r_{0}$ はシュバルツシルト半径より内側の座標だから $r_{0}<a$ である.結論はこうなる. 色々と論じることは出来るかも知れないが,百聞は一見に如かずだ.この式のグラフはこんな形になる.

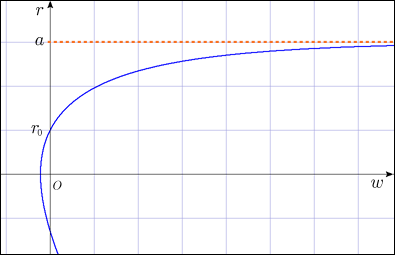
今はこのグラフの r>0 となる領域にしか意味はないのだが,参考までに下の方まで描いておいた.

横軸が時間経過を表している.つまりブラックホール内の光は,幾らの年月,外で待ってみてもシュバルツシルト半径より上には決して這い上がって来れないことを意味している.これが望んでいた答えだ.

次回予告

ブラックホールの内部の様子を知るには別の座標系を導入しないとダメだと聞いた.そこで私はそれを易しく説明してみようと思い立ち,勉強しながら今回の記事を書き始めたのである.ところが本題に入る前に別の疑問にぶつかってしまった.

別の座標系を導入しない場合にはどの程度のことが分かるのだろうか？

何しろ,私が参考にした教科書の説明は少々入り組んでいて,どこまでが新しい座標系を取り入れたことによって分かる成果なのか,どうもはっきりしなかったのである.まずはそこからだ.

それを書くだけで分量が多くなって行き,今回のような結果になったというわけだ.しかも相対論の記事を久しぶりに書いたので,以前に書いた内容を忘れてしまって,同じ内容を再び繰り返すことになってしまった.冗長かも知れないが,復習だと思ってほしい.

わざわざ別の座標系に頼らなくても,思っていた以上に色んなことが分かってしまうもんじゃないか,というのが感想だ.となると,別の座標系を導入することの意義は何だろうか.それは次回のお楽しみである.

それにしても,最後にやった「光が出てこれないこと」についての説明で少々引っかかることがある.そこでは,ブラックホールの外側の無限遠を基準にした時刻を使い, w=0 において,シュバルツシルト半径よりも内部にあって上向きに飛んでいる光が $r_{0}$ の位置にあると仮定したのだった.しかし「ブラックホールの内部のことは外側からは一切知ることができない」のではなかったか.「ブラックホールの内部はもはや我々の知り得る宇宙とは分離した別世界だ」と論じている書物もあるくらいだ.だとすると,ブラックホールの外側を流れる時間を使ってブラックホールの内側にある光の運動を論じることに意味があるのだろうか.

意味はある,と答えよう.この外から見ている w=0 の瞬間,内部の $r_{0}$ という場所に実際に光があるかどうかは分からない.上を向いているかどうかも分からない.しかし仮定の話をしているのである.もしそこにあったらその後どうなるのか.我々の使っている「外側の時間」で測って何秒後かにその光に会えることになるのかどうか.それを知りたかっただけなのだ.結論は,決して会えない,ということだったが.

ただ,少し気を付けないといけないことがある.今回の説明を読んだだけだと,間違ったイメージを描いてしまう可能性があるのだ.ブラックホールの内部から外側に向けて放たれた光は,永遠にシュバルツシルト半径付近の内側で停滞しているというイメージをすでに持ってしまってはいないだろうか.これは飽くまでも,外部にいる人にとっての解釈なのである.

内部に落ちた人の視点ではさらに驚くことが起きている.しかし,それを考えるのは今の座標のままでは難しい.次回でそれを考えることにしよう.今回計算した光の正体を知ることになれば,きっと驚くことになると思うのだ.