相対性理論：負の曲率を持つ宇宙

よく見かける図はどうも嘘っぽい

前回の話の続きである.

宇宙はどの場所でも同じであり,全体で同じような曲がり方をしているに違いないという発想から始まり,それは球の表面のようなものに違いないというイメージを経て,ロバートソン・ウォーカー計量が導かれたのだった.しかし宇宙全体で曲率が一定になるような形というのは球面だけだろうか.

球面の曲率は正の値であった.そしてもし曲率が 0 ならばそれは平面のことであり,球の半径が無限大になった状況を考えるのと同じようなものである.これ以外のことを考えようとすれば曲率が負になる状況だろう.

曲率が負になるような曲面というのは次の図のような形が例として良く挙げられている.

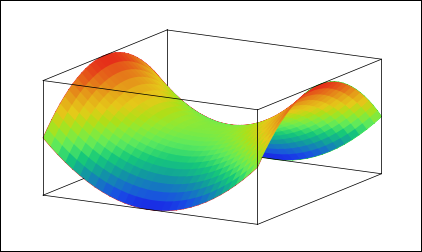
図の中央付近を見ると分かりやすいのだが,ある方向については山の頂上のようになっており,違う方向を見れば谷底のようになっている.方向によって湾曲の仕方が逆になっているのである.それが負の曲率を持つ面の特徴だ.

しかしこの図を見る限り,中央部分だけが特別な点であるように思える.曲面のどこを見ても曲率が負になっているのかも知れないが,全面で一定の曲率になっているようには思えないのである.もし宇宙がこの図のようになっているというのなら,宇宙には特別な点があることになりそうだ.それは望むような宇宙のモデルではない.

果たして,宇宙全体で曲率が負で一定であるような形状は考えられるのだろうか.そしてそれは図示できるようなものだろうか.

リバース・エンジニアリングを楽しむ

すぐにイメージすることが難しいものでも数式に頼ればヒントが得られることが多い.数式を解釈することで何とかイメージできるかも知れないし,できないようなものなら仕方がない.

曲がった 3 次元空間というのは 4 次元の中でしか表せないのでどうせ図示はできない.曲がった 2 次元空間ならば 3 次元の中に表せそうだから,とりあえずはそこを目標にしよう.次元が小さい方が数式も複雑にならなくて助かる.

前回の話で,曲率が宇宙全体で正で一定であるような 2 次元の計量は次のように表されることを導いたのだった. 曲率が負になるような計量を作りたいのであれば,話は簡単だ.この式のまま, K<0 だと考えてやるだけでいい.が負になったからといって計算内容に変わりはなく「至るところ負で一定」だという答が出るはずだ.

しかし式の形が前と変わらないのでは取っ掛かりがつかめない.前回の話では曲率と球の半径との間に K=1/R^2 という関係があるとしていたが,これの符号を変えて K=-1/R^2 としたものを代入して使うことにしよう. が実数だとすればこうすることでが負であることを表せるだろう.しかし前回のと今回のは別物だと考えた方がいいかも知れない.それでも,前回と対比することで話を進めたいので,わざと式を似せるために同じ記号を使うことにする.

さて,この (2) 式のような計量が導かれてくるためにはどのような座標を採用すれば良いかというのを考えてみよう.前回の話を逆にたどるわけだ.

前回の話を軽く復習しておこう.球面の計量というのは次のような形をしていたのだった. それを ρ = Rsinθ という関係を使って書き換えたら (1) 式が出来たのである.その計算過程は次のような感じだった. ということは・・・.この最後の式のカッコの中身のマイナスの部分がプラスになるような変換を考えてやれば (2) 式になるのではないか？もし双曲線関数というものの性質を知っていれば話は簡単だ.知らなければ思い付くのは難しいかも知れない.

双曲線関数というのは三角関数によく似た性質を持っているのだ. な,すごく良く似ているだろう？ (x,y)=(cosθ,sinθ) という式を作れば円が表せるのと同じように, (x,y)=(coshθ,sinhθ) という式を作れば双曲線が描けるのである.故に双曲線関数と呼ばれる.

要するに ρ = Rsinθ という関係を当てはめる代わりに,双曲線関数を使った ρ = Rsinhθ という関係を当てはめれば良かったのではあるまいか.試してみよう. ほらね,うまく行った.変更点はこれだけでいいのだろうか？この結果を (3) 式に当てはめれば (2) 式が導かれてくるか,というのを見てみよう.うーん,無理だ.それほど甘くはない.なぜ無理なのか,読者も試してみて欲しい.問題点がはっきり見えてくるはずだ.しかし,(3) 式の代わりに次のような形をしていればうまく行くのではないだろうか. どこが違うか分かるかな？ sin^2 θ だった部分を sinh^2 θ に変えたのだ.さあ,核心に近づいてきた！この形の計量を実現するような座標変換を見出すことが出来ればいいのである.これは球面の計量によく似ているし,違いと言えば sinθ が sinhθ になっていることくらいだ.だから,普通の極座標の変換式を少しだけいじった次のような変換を使えばいいのではないだろうか. (5) 式から (4) 式が出てくるかどうか,実際にやってみるといいだろう.途中までは「おっ,いい感じか！？」と思わせてくれるのだが,最後の最後に裏切られるはずだ.我々が普段当たり前だと考えている次のような関係を前提として計算したのではうまく行かないのである. こうではなくて,次のような形になっていればうまく行くのになぁ,と思うことになるはずだ. 何だ,この変な形の計量は？せっかくここまで来たけれど,とんだ見当違いだった.こんなものは使いものにならない・・・と思うかも知れない.

しかしこれこそが答えなのだ.一つの座標の項だけが負になっており,特殊相対論に出てきたミンコフスキー時空の計量を思い出させる.ミンコフスキー時空の場合には負になっている項は時間軸だったのだが,ここでは空間の軸の一つだけが負になっているのである.

我々が探していた,全面で曲率が負で一定になるような曲面というのは,「3 次元のミンコフスキー空間内に存在する 2 次元曲面」だったのだ.これでは普通の空間には描けなくても当たり前ではないか！

しかし全く無理なわけでもない.このイメージをできるだけ分かりやすく伝える努力をしてみよう.

遠くへ行くほど広くなる世界

しかし図を描く前に数式について軽く整理しておこう.負で一定の曲率を持つ 2 次元曲面の計量は (2) 式と (4) 式であり,どちらも表現が違うだけで同じものである.

(2) 式は円周の長さが 2πρ になるように工夫した動径目盛りを採用しているが,このは実際の距離を表してはいない.また (4) 式にはが出てくるが,双曲線関数で使うというのは特にどこかの角度を表しているわけではない.どちらの式も直観的だとは言えないということだ.

すると 2 次元人にとっての実際の長さを使って表した計量がどうなるかというのも見ておきたくなる.それは簡単に導ける.(4) 式で dφ=0 とすれば動径方向の変化だけを表すことになるだろう.そのときのがに一致するはずだから r = Rθ という関係があるということだ.これを使って (4) 式を書き換えればいい. この式からこの 2 次元世界に描いた円の円周の長さが計算できるのだった. dr=0 と dφ=2π を代入してやればいい.円周は 2πRsinh(r/R) であると求まる.

sinhθ の性質を調べてやると分かるが,そのグラフは指数関数的に増加する形である.つまりこの世界での円周は,半径が大きくなるほど急激に増えるのである.半径が増えるに従い,円周率の値が増加しているということになる.曲率が正の世界とは全く逆の光景だ.

3 次元の世界でも,もし我々の宇宙の曲率が負なら似たようなことが起こるだろう.まず,自分のいるところから一定の距離にある壮大な天球を考える.その天球に畳か何かを敷き詰めるなどして面積を実際に測ってみると 4πr^2 よりも遥かに広いのである！遠くへ行くほどに広がっている世界・・・.なぜ？どうなっているんだ？その広い世界はこの有限の視界の中にどんな風に畳み込まれているというんだ？常識で考えて,そんなことは無理だろう！？

このようなことが起こる仕組みは最初に描いた図でも説明できる.2 次元人にとっては自分たちの世界の上にきれいに輪を描いたつもりでも,3 次元人にとってみればその世界自体が上下に湾曲しているのだから,そこに描かれた輪もウネっている.

中心から円周までの距離がどこを測ってもであったとしても,このようなウネった円の円周は当然 2πr よりも長くなるわけだ.

それでも私は最初の「馬の鞍」のような図には不満があるのだった.面の全体が均等で平等であるようには見えないのだ.全面で曲率が一定であることがはっきりと分かるような,負の曲率の宇宙を表すための,もっといい表現はあるだろうか.

イメージを描く

我々が考えようとしているのは曲率が負で一定となるような面であり,そのためにはは宇宙のどこでも一定であるべきだ.(5) 式を使ってが一定であるような面を図示してみよう.本来はミンコフスキー的な空間の中で実現している図形であるが,そんなものは描きようがない.だから実際のところは無視してとりあえず普通の空間の中に描いてみるのである.

そんなに難しい知識は必要ではない.(5) 式で x^2 +y^2 を計算してみれば R^2 sinh^2 θ となるだろう.つまり面内だけで見れば,半径が Rsinhθ で表されるような円になる.

そして座標が Rcoshθ である.つまり面内の円の半径と座標の関係が双曲線になっているのである.真横,つまり面や面から見れば双曲線になっているわけだ.

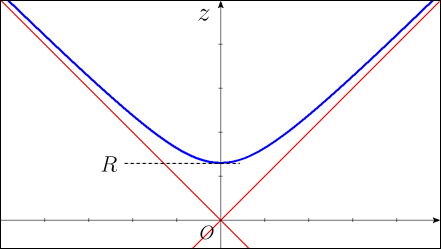
つまり,描くべきは双曲線の回転体である.

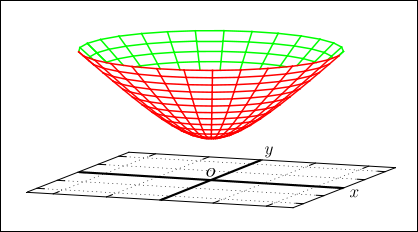
こんな図を見せられても,曲率が正の,割りと普通の曲面でしかないではないかと思えるだろう.しかもどの地点も対等であるという感じもしない.しかしこれはミンコフスキー的な空間の中にあるものだから距離の概念が普通の感覚とはまるで異なっているのである.そこが面白いところだ.

この空間内では面の方向への移動に対しては普通の距離の概念を当てはめることができる.しかし方向の動きがある場合,その分を差し引かなくてはならないことになる.ということは,この世界の中ではどれだけ進んでも距離が 0 という状況だって起こりそうだ. ds^2 =0 となる場合を考えれば分かるだろう.(6) 式によれば,それは dx^2 + dy^2 = dz^2 となる場合である.それは原点を頂点として上に伸びる円錐面,すなわち真横から見れば斜め 45°の方向に伸びている面である.特殊相対論に良く出てくる光円錐を思い出すような話だ.

ちょっと寄り道して,この不思議な円錐面について考えておこう.この円錐面の上では全ての点の距離が互いに 0,すなわち全てが同一地点だと解釈できるということだろうか.いや,そうではない.原点の方向に一直線に向かう時には距離は 0 であるが,それ以外の場合には 0 ではないからだ.これは厄介である.互いの距離が 0 であるような 2 点は同一点だと考えないと色々と不思議な現象が起こるのだが,それができないのである.例えば円錐面上の 2 点間を移動する時には,直接向かえば距離が離れているのに,原点を経由すればどの地点へも距離 0 で行けてしまうことになる.寄り道すれば必ず遠くなるという「三角不等式」が成り立っていない世界なのである.しかしこれはすべて円錐面の上だけの話である.

幸いなことに,そういうややこしい問題に関わる必要はなさそうだ.今我々が考えようとしている 2 次元の住人は先ほどの図に表した双曲回転体の面上にだけ住んでいて,彼らはこの厄介な円錐面に触れることは決してないからである.しかし双曲回転体というのは原点から離れるほど,この円錐面に漸近する形で存在している.このことは重要である.つまり原点から離れるほどに円錐面に似た性質が出てくるということだ.

さあ,ここからは肝心の双曲回転体の面上でのことに集中することにしよう.今後はこの 2 次元世界「双曲回転体の面」のことを略して「双曲面」と呼ぶことにしよう.

まず気になるのは,この双曲面の上で移動した場合, ds^2 がマイナスになったりすることはないのか,という点だ.しかしそれについては心配ないことがすぐに分かる.もしも双曲面の傾きが z=0 の面（図で言うところの水平面）から 45°よりも急になることがあれば,面内の移動よりも方向の移動の方が大きくなることになるだろう.しかし双曲面は原点に最も近い部分では水平であるし,そこから離れるほどに急な斜面にはなってゆくが,45°の円錐面に漸近するだけである.よって 45°を超えることはない.この面上では扱いに困るほどのおかしなことは起きないと断言できる.

次は最も大事な点だ.双曲面上の点は (5) 式で表されているわけだが,それぞれの点と原点 (0,0,0) との距離を確認しておこう.ここで言う距離というのは (6) 式を使って計算する,この世界での距離のことである. うっ！マイナスか！？しかしミンコフスキー的な空間においては ds^2 が負になることは珍しくもないのだった.原点から双曲面上の点まで引いた直線はどこであっても 45°より急になるわけだからまぁ予測できたはずのことだ.

ついでに今更ながら気付いたのは,この双曲面というのは, x^2 +y^2 -z^2 =-R^2 ,つまり, を満たす点の集合であると表すこともできるんだなぁということだ.まぁ,双曲面なんだから当然か.今更すぎる.

いや,そんなことよりも,見るべきことがある.どの点までの距離も等しいということだ.図の中の表現ではどこまでも離れていくように見えていても,この世界の中では双曲面上のどの点も原点から常に等しく同じ距離にあるというのである.これぞ,この世界の全ての点がどれも平等であることの現れである.どこまで行こうとお釈迦様の手の上というか,そういう安心感がある.このことを確認しただけで,私の心のモヤモヤは吹っ飛んだ.

このの値が大きくなるほど双曲面は原点から遠ざかり,平らに近くなってゆく.今回は曲率との関係を K=-1/R^2 としたが,はちゃんと 0 に近付くわけだ.平らな空間というのは今回のような負の曲率の空間の極限でもあるわけだ.（双曲線はがどこまで大きくなっても双曲線のままだという気がするが,それを言ったら球だって半径が無限大になっても球状に曲がっていること自体は変わらないのだからどっちもどっちだろう.）

ところで,この双曲面の上に住んでいる住人にとってはこの双曲面はどのように見えているのだろうか.図の中央付近から離れるほどに円錐面に近付くことになるのだから,円錐面と似た現象が現れるようになる.つまり,我々にとって長い距離に見えていても,彼らにとってはずっと短い距離に感じられるのである.「中央の点からはまだほとんど離れてはいない」とか言いながらグングン外側へと歩いて行ってしまうのだ.そして彼らは驚くことだろう.「まだ中央からはほとんど離れていないというのに円周を測るとなぜこんなに長くなってるんだ！」と.実は中央からかなり遠く離れたところに立って,こんなことを叫んでいるのである.

このように,曲率が負の世界は閉じておらずどこまでも無限に広がっている.曲率が正の世界は閉じていて有限の広さだったが,そこが大きな違いだ.

我々の宇宙は開いているのか,閉じているのか,一体どちらだろうか.