相対性理論：加速系の座標変換

本記事の動機

一般相対論というのは,「星の質量に引かれることによる真の重力」も,「加速することで感じる擬似的な重力」も,どちらも同じように座標変換によって生じる力として説明してやろうというものだった.真の重力が時空の歪みによって作り出されていることは分かった.一方,加速運動している人は,周りに星なんか無い場所であっても,重力らしきものを感じている.彼らにとっては時空が曲がっていると解釈できるという事なのだろうか？

それを調べるために,静止している自分と,加速しているロケット内の立場での座標の変換が一体どうなるかを考える事から始めてみよう.慣性系どうしの間の座標変換はローレンツ変換であった.相手が加速しているからには,ローレンツ変換以外の何らかの変換になるのだろうが,それはどう考えたらいいのだろう.

ロケットが一定の加速を続けていて,ある速度になった時に突然加速をやめたら,その瞬間から慣性系に戻るだろう.その時にはローレンツ変換が使えるはずだ.では加速を切った瞬間に,いきなり変換のルールが大きく変わってしまうものだろうか.いや,加速中には速度 v が変化してはいるが,次々と慣性系を乗り換えているだけだと考えられるから,その一瞬一瞬にはその時点の速度でのローレンツ変換が適用できるに違いない.

とは言うものの,ロケットの移動に合わせて刻々と変換のルールが変わる座標変換なんて一体,どんなものを考えたらいいのだろう？時空図の全面を覆ったローレンツ変換のひし形が徐々にひしゃげて行くイメージから離れられなくなってしまった.

相対論では時間も空間も時空図の上で表現できるはずだった.なのに,徐々にひし形がひしゃげることを考える時,時空図の上に無い時間で物事を考えている事になる.こんな考えは絶対におかしい.

そんな時,「リンドラー座標」というものに出会った.その図を見た瞬間,探していたのはこれだと思った.

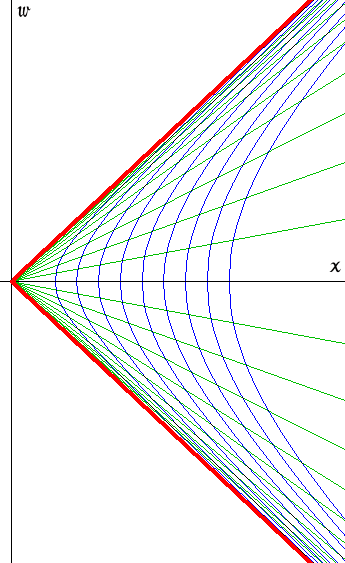
これは,一定加速度で進むロケットの系と静止系との関係を静止系の立場で表したものとなっているらしい.確かにローレンツ変換に似たひし形が無数にあって,時間の経過と共にひしゃげて行っている.こんな表現の仕方が可能だったとは・・・.しかし一体どういう考えでこうなるのだろう.

一定加速の軌道はどう表されるか

この座標が本当に今の目的に合ったものなのかを調べてみよう.加速系の座標を (x',t') で表すことにする.ロケット内の人は加速系の原点 x'=0 にいて,自分は動いていないと思っている. x'=0 の線を静止系の時空図の上に描いてやれば,それが軸を表すことになるはずだ.静止系から見れば,それはロケットの飛跡に他ならない.

ここでまたもや壁にぶつかる.そもそも一定加速度とは何だろうか.これは静止系にいる人から見れば一定加速にはならないだろう.もし速度が文字通り一定ずつ加わるならばいつか光速を越えてしまうからだ.運動量を一定量ずつ増加させていると考えれば良いのだろうか.だとしても,その増加の割合は加速している人の時計で測るべきなのかどうか？加速している人にとっては自分こそが静止しているので自分の運動量が増えているとは考えていないだろう.誰の立場でどう考えたらいいのだろう.

落ち着いて考えてみよう.すでに速度のロケットがあるとする.彼らの時計で dt' だけ経過する間に dv' だけ速度を増すときに彼らの感じる加速は dv'/ dt' であり,今の場合はこの値が一定値になっているというわけだ.この状況を静止系からの視点に切り替えて考えてみたらいいのだろうか.

ああ,そうか！まさかこんなところであの計算が役に立つとは思わなかった.ニュートンの運動方程式をローレンツ変換したときのあの式だ.（申し訳ありませんが,その記事はまだこのサイトにはありません.）今の話に合うように記号を変えてある.この式の中にあるは,系から見た物体の速度を意味している.今はロケットの速度は静止系から見てであるから,系から見れば v'=0 である.つまり,静止系から見たロケットの速度変化は,次のように表せるということになる. これを微分方程式として解いてやろう. t=0 の時のロケットの速度が 0 だと考えれば積分定数は 0 になるので, となる.これをさらにで積分してやればロケットの軌跡 x(t) が求められる. t=0 での座標原点を互いに合わせる為には,積分定数を C'=-c^2/a と決めてやればいいのだろうが,今は敢えてそれをしない.なぜなら C'=0 としておけば,これは典型的な双曲線の形になっているから,しばらくはそうした方が扱い易いのである.時間を w=ct で置き直して変形してやればもっとすっきりする. これに合わせて,今後は加速系の座標の方も (x',w') で表す事にしよう.

双曲線の平行移動ではダメなの？

x'=0 を表す線はこうして求まったが, x'=1 とか x'=2 とかの線はどう描いてやろうか. t=0 にはロケットの速度は 0 なので,加速系と静止系とは同じ視点にいることになる.だから静止系が見る軸の目盛りと加速系が見る軸の目盛り幅はこの瞬間には一致していることが言える.ということは,今求めた双曲線を軸方向へ等間隔に平行移動してやるだけでいいということになるだろうか.

これは複数のロケットを進行方向に一列に等間隔で並べておいて,一斉に同じ加速度で出発させることに等しい.どのロケットも常に同じ速度になるはずだから,ずっと同じ間隔が保たれるはずだ.いや,ちょっと待てよ.本当にそうだろうか.確かに静止系から見ればそうなるが,加速系では同時刻を表す軸が徐々に傾いて行くことになる.だとすると,静止系から見ると違う時刻にあるロケットたちを,加速系では同時刻に存在するロケットだと判断するようになるのであろう.だから今考えたような状況を加速系から見れば,他のロケットたちは自分とは違う速度で移動していると感じるはずだ.つまり,互いの距離が変わるように感じるだろう.今は加速系で見た場合に距離が等間隔で常に変わらない線が欲しいのであるから,そのような一斉に同一の加速をするロケット群の軌跡は,ロケットにとっての座標の基準には出来ない.うーん,簡単には行かないものだ.

同時刻線を描く

ではこの問題よりも先に,ロケットにとっての同時刻線,すなわち軸がどうなるかを考えてみよう.加速系であっても,瞬間瞬間にはその時点での相対速度でのローレンツ変換が成り立つはずだという考えは先に話した.ローレンツ変換では軸の傾きと軸の傾きは逆数の関係にあるのだった.つまり,先ほど求めた x'=0 を表す双曲線の傾きを求めてやってその逆数を取れば,それが同時刻線の傾きを表すことになる.軸上の各点において,そのような条件を満たす傾きを持つ線が交わることになるのである.計算してやると分かるが,双曲線上の点の座標を (x,w) とした時,今求めたい線の傾きはちょうど w/x となるのである. これは面白い.つまりこれは,静止系の座標原点から双曲線上の各点へ向って直線を引けば,その傾きは自動的に同時刻線の条件を満たすという事になるわけだ.

しかし,この直線は同時刻線そのものだと考えていいだろうか.たまたま双曲線上ではそうなのであって,同時刻線が直線で表せるという意味にはならないのではないだろうか.確かにローレンツ変換では同時刻線は直線であった.しかし今は軸でさえ曲がっているのであるから,このことも疑ってみるべきだろう.

もし加速を止めたなら,その瞬間からは確実に通常のローレンツ変換が適用されるのであり,その場合の同時刻線は直線で表されることになる.今の疑問は,加速を止める直前直後で,この線に変化があるかどうかだ.「今同時だ」と言っていた座標上の各点の出来事が,加速を止めただけで「今はもう同時ではない」となるかどうか.そんなのは矛盾であるように思える.この人にとってどっちの今が今なのだ？今というのは一点であって,今しかないだろう.このことから,私は加速中でも同時刻線は直線で表していいだろうと考える.

しかしこれだけで全ての読者に十分納得してもらえる自信がないので,この辺りはそれぞれでじっくり考えてもらいたい.軸の方について言えば,こちらは加速を止めた瞬間から直線に変わり,それまで「私にとっては同じ場所だ」と主張していた未来の各点が,一瞬にしてそうではなくなるのである.一方を認めて他方を認めないというこの説明はどこか一貫性がなくて説得力が無いような気もする.当たり前に感じることほど,ちゃんとした説明は難しいものだ.

とにかく同時刻線が常に直線で表せることを認めると,物理的にはすごい事が起こっていることが読み取れる.あらゆる同時刻線が静止系の座標原点に集まっているのである.この点は加速系にとってはいつまで経っても今のままであり,この点の未来を見ることが決してないのである.凍りついた世界だ.しかもこの点から出た光の軌跡は図の上で45°の傾きの直線で表されているが,軸はそれに漸近する形になっているのであり,決してロケットに追いつく事がないことを意味している.光はこの点より後方からは決してロケットには届かない.ブラックホールに似た状況が生じているのである.それでこの現象は「ブラックウォール」と表現されることがあるようだ.こういう話ももっと分析していくと色々と面白いことが出てくるのだが,脇見はしないで元の目的に返るとしよう.

加速系の固有時を求める

次に自然に知りたくなって来るのは,どの傾きを持つ同時刻線が,ロケットにとってのどの時刻に相当するかという関係だ.先ほど見た座標変換の図を,ちゃんと数式によって表現してやりたいのだ.加速系での時刻経過を知るためには, x'=0 の双曲線に沿って固有時を積分してやればいいだろう.

その為には次のような考え方をする. w=0 からスタートして双曲線に沿って微小距離だけ移動する時,静止系の座標ではそれぞれの軸方向へ,だけの変位があるだろう.この時の固有時の変化は次のように表せる. よっての変位のみに注目して,これを 0 からまで積分してみるだけで良い. この積分では双曲線関数の逆関数についての次のような公式を利用した. というのは,ロケットの人にとっての経過時間のことに他ならないので,積分定数を 0 と置いてスタート時の時刻を一致させる.この計算でとの間の関係式が得られた事になる.双曲線関数の逆関数なんてものが出てきて話がややこしくなってきたが,次のように表しておけば,とりあえずは逆関数は使わないで済むだろう.

変換式の完成

ここまで考えれば,先ほど手が出せなかった内容についても割と簡単に理解できるようになっている.加速系にとって距離が等間隔であることを保つ線はどう描けるかという問題だ.通常の慣性系どうしのローレンツ変換の話から類推してみればいい.運動する系から見て相対速度0で運動する,離れた場所の物体の軌跡は,同時刻線に対して x'=0 の線が交わるのと同じ角度で交わっているはずだ.

だから今の場合も,ある同時刻線上に注目した時に, x'=0 の線がそれと交わる角度と同じ角度を持って交わるような曲線群がそれであるだろう.どの同時刻線に注目してもそのようになっているべきである.つまり,どの曲線を見ても,その上のある点での曲線の傾きと,静止系の原点からその点まで結んだ直線の傾きには逆数の関係があることになる.結局のところ,それらは x'=0 の場合と漸近線を同じくする双曲線群のことではないか！

これだけ知っていればもうグラフは書けるし,座標変換の関係を数式で表せるはずだ.

ここで双曲線関数についての次の知識が役に立つ. という双曲線は,媒介変数を使えば, と表す事が出来る.

ということは,(1) 式で表された x'=0 を意味する曲線は, と書けるはずだ.この曲線は w=0 において x=c^2/a を通るのであるから, x'=1 を表す曲線は w=0 において x=c^2/a +1 を通るような双曲線であるべきだ. x'=2 の場合も x'=3 の場合も同様である.つまり,次のような式で表されるはずだと言える. この時,媒介変数がの関数になっているのは想像が付くと思うが,果たしての関数にはなっていないのだろうかという点が心配になる.ところがもしそうだとしたらおかしいのである.を一定にしてだけを変化させるとき,点 (x,w) は同時刻線上をまっすぐ進まなければならないはずである.がの関数だとしたらそうはならないではないか.

では q(w') は具体的にはどんな形になっているべきだろう.これについてはもう答えが出ている.(2) 式と見比べてもらえば一目瞭然だろう.これで我々は最終的な答えを得た. これが欲しかった関係式である.もし w=w'=0 における軸の原点を合わせたければ,から c^2/a だけ引いてやればいい.

なぜ彼らは同一の系なのか

これで万事解決のようではあるが,まだ腑に落ちない点を感じている人がいるはずなので少しだけ補足しておこう.まず注意しなければならないのは,この変換が, x'=0 にいて加速度を感じている人にとっての変換に過ぎないという事である.

x'=0 より右側にある双曲線を見てもらうと分かることだが,この双曲線のような移動をしている人はよりも小さい加速度を感じている.また図には描かれていないが, x'=0 より左側にも双曲線はあって,それに従って移動している人は,よりも強い加速度を感じている.彼らだけが見る「ブラックウォール」の付近にいる人は猛烈な加速度を感じながら付いて行っていることだろう.そして彼らにとってはそれより向こうはない.

それぞれに違う加速度を感じている人たちが等間隔で並んでいる状況であるにも関わらず,彼らが互いに互いのことを「自分と同じ系にいる」と主張するのは奇妙な事に思える.このことを説明しておこう.

実は今回出てきたというのは加速度を感じている人にとっての時間でしかない.この図には同時刻線が引かれており,これは確かにそれぞれの双曲線上にいるどの人にとっても共有される同時刻線には違いないのだが,この線は決して,それぞれが感じている固有時間が同じになる点を結んだ線ではないのである.彼らは互いに異なった時間経過を感じているということだ.

そのずれ具合がどんなものかを計算してみよう.まず x'=0 にいて加速度を感じている人の固有時と同時刻線の傾きの関係は, と表される.そして x'≠0 にいる人にとっての固有時 w'' との関係については, c^2/a の部分を c^2/a +x' に置き換えてやればいいので,次のようになるだろう. これらの式の右辺のカッコの中が等しいということなので,次の関係が導かれる. x'=0 にいる人は x'>0 にいる人について,「彼らの時計は早く動いている」と感じるし, x'<0 にいる人については「彼らの時計はゆっくりだ」と感じていることになるわけだ.そして次のように解釈することだろう.「この系にはどこでも一様にの加速が働いているのだが, x'>0 にいる人の時計は早いので,この加速の勢いをゆっくりだと感じてしまうのだ」と.そして x'<0 については全く逆の説明になる.この系に所属する彼らの全てが次のように解釈している.「自分の感じている加速こそが本物で,それと同じ加速が同じ系にいる人たち全体に同じように掛かっているのだ」と.そういう意味で彼らは「同じ系の仲間たち」なのである.

一般相対論にあてはめて確認してみる

求めた変換式を使って,計量を計算してやろう. であることから,これを無限小線素の式に代入してやれば, という具合に,変形過程はすっぽり省いているが,意外に綺麗な形にまとまる.

$\met{0}{0}$ の -1 からのズレが,彼らの感じる重力の存在を意味しているという一般相対論で使った説明がこの場合にもちゃんと当てはまっている.一様重力によるポテンシャルは φ=ax であるが,近似的に $\met{0}{0} ≒ -1-(2/c^2) φ$ という関係が成り立つという説明と矛盾しない.また,加速系内での位置によって時間経過が異なる度合いは, $√(-\met{0}{0})$ とピッタリ一致することが分かるだろう.重力場の中で下方にあるほど時間の流れが遅くなるという一般相対論の結果も,同じように適用されるわけだ.

今回の座標変換は平面グラフの上で説明できたのだから,この計量を使って曲率を計算してみたところで当然の如く 0 となるだろう.実際にやってみたが,確かにそうなった.

加速によって擬似的な重力を感じていたとしても,時空は曲がってなどいないということだ.それは誰から見ても曲がっていない.一方,真の重力がある時には時空は曲がっている.誰かの視点による見かけだけの話ではなくて,確かに曲がっている.

今回の話では,最後に一般相対論に当てはめて確認してみたけれども,それ以外では一般相対論の知識は何も必要ないのだった.つまり,一般相対論は特殊相対論の拡張になっていて,慣性系や加速系をも包括して扱える形式を用意しているけれども,その本当の価値は,真の重力場を記述する時にこそ発揮されるということだろう.

一般相対論は本当に「重力の為の理論」であるというわけだ.