熱源が二つだけの機関
熱力学の第 2 法則では仕事と熱に関する表現が出てきており,熱機関を意識したものになっている.熱機関について考察することで,第 2 法則を表現する数式を見つけることが出来るかもしれない.なるべく単純なものから考えていこう.
一つの熱源だけで動作し続ける機関はトムソンの原理に引っかかるので考えるだけ無駄だろう.よって一番単純な熱機関は二つの熱源（高熱源と低熱源）の間で動作するものだということになる.その動作を図にすると次のようなサイクルになる.
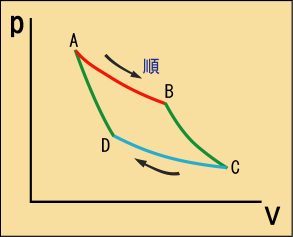
これは「カルノーサイクル」と呼ばれるものである.右回りすれば,高熱源から熱を受け取り,その一部を仕事に変えて残りの熱を低熱源に捨てる動作をする.また準静的過程であるので逆回りも可能であり,仕事を加えることで低熱源から熱を拾って高熱源へとくみ上げる動作をさせることも出来る.この二つの動作を区別するために,前者を「順カルノーサイクル」後者を「逆カルノーサイクル」と呼ぶことがある.
赤と青の線で表した部分は等温変化であって,熱源が二つあることに対応している.これらは反比例のグラフになるはずなので,かなりデフォルメされている図であることが分かる.正確に描こうとするとかなり細長くなってしまって格好が付かないのでわざと崩してある.赤線が気体が高温側に接して熱平衡を保ちながら変化する状態,青線が低温側に接している状態を表している.それぞれの熱源は非常に大きくて,少々の熱が移動したくらいでは温度は変わらないとする.
この二つの温度の間を熱平衡を保ちながら変化させるには断熱変化しかありえない.もしこの変化の途中に外部との熱のやり取りを行わせるならば,熱平衡を保つために外部の温度をシリンダー内の気体と同じ温度にしなければならず,外部の温度を徐々に変化させる必要があるだろう.それでは「二つの熱源のみ」を考えた意味がない.
ところで,先ほどはトムソンの原理に反するからという理由で考えるのをやめたが,一つの熱源のみと断熱変化の組み合わせでは輪が作れないのは明らかだろう.
カルノーサイクルが大切な理由
このような単純な機関を考えたところでとても現実からは掛け離れていて役に立ちそうにもないと思うかもしれない.ところが次の図を見てもらいたい.
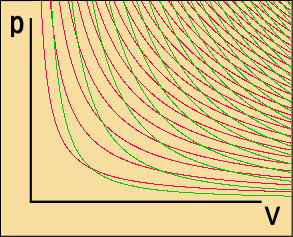
沢山の等温曲線と沢山の断熱曲線が描かれている.こちらは割と正確に描いた線だ.そしてその中に大小さまざまなカルノーサイクルがあるのが分かるだろう.これらの線はもっと細かく描くことも出来るが,等温曲線どうしは決して交わることはないし,断熱曲線どうしも同じである.よって無限に細かい多数のカルノーサイクルが描けることになる.
つまり準静的過程である限りはどんな形のサイクルであろうと,このひしゃげた細かい網目の組み合わせで表現できてしまうのである.このことをどうやって応用するかはその時に説明するが,とにかくこれからやることはもっと広い範囲のことを説明するための大切な基礎部分であることを頭に置いていてもらいたい.
カルノーサイクルが理論上だけの存在で,現実には存在しないものだという誤解もなくした方がいい.カルノーサイクルは理想的なものではあるが,それにいくらでも近い状態を作り出して実験することが可能なのだ.準静的過程を保つために数日かけて 1 サイクルを実現するようなカルノーサイクルの実験装置も存在している.科学は絶対に実験を通して検証することが必要だという態度が頑なに守られていることが分かる話である.
カルノーサイクルはみんな同じ？
一口にカルノーサイクルと言っても,その作りは様々だ.使う気体は理想気体に限らない.気体の種類が変われば,同じ等温曲線と言ってもグラフ上の形は微妙に違ってくるだろうし,どの圧力の時にどの体積まで縮めるかという選択によってもグラフ上のサイクルの形は色々なものが考えられる.グラフ上で一周するときに囲まれた面積が,機関が 1 サイクルで行う仕事を表しているが,その面積もやり方によって色々な値を取ることになるだろう.たとえ同じ面積であってもその実現方法はさまざまである.
ところが面白いことに,高熱源の温度
と低熱源の温度
さえ決めておいてやれば,どんな動作をさせようともこの機関の熱効率はどれも変わらないというのだ.それは難しい理論を使わなくても簡単に証明することが出来る.ただし,証明の途中で表れる結論も大事なので,4 つの段階に分けて説明するとしよう.
(1) 高熱源の温度と低熱源の温度,そして仕事量 さえ決めておけば,1 サイクルで高熱源からもらう熱 と低熱源へ捨てる熱 の値は決まってしまう. |
これを証明するのは簡単だ.まず 2 種類のカルノーサイクルがあるとする.ただし,1 サイクルでする仕事は両方とも同じだとする.一方を順カルノーサイクルとし,もう一方を逆カルノーサイクルとして動かす.そして一方が生み出した仕事を利用して逆カルノーサイクルを動かすことを考えよう.全体として見れば,熱の出入りしかないように見える.
もし順カルノーサイクルが高熱源からもらう熱量より,逆カルノーサイクルが高熱源へ返す熱量
の方が多ければ,クラウジウスの原理に反する装置が出来てしまうことになる.そんなものがこんな簡単にできれば苦労はしない.その逆ならば,高熱源から低熱源へ熱が移動しただけであって,それは不可逆過程のはずだ.カルノーサイクルは可逆なので,逆に回せばやはりクラウジウスの原理に反してしまうことになる.
つまり,
でなければならず,やり取りする熱量はカルノーサイクルの種類によらないことになる.についてはエネルギー保存からとの差で決まる.
これで第１段階は証明できた.次へ行こう.
| (2) との比は,には依らない.とだけで決まる. |
先ほどの (1) の結論はとはそれぞれ,とととの関数になっているということである.
ところで,今,同じカルノーサイクルを
個並べて動かせば,全体として
の熱を受け取って
の仕事をする装置が出来上がるはずだ.これは次のように表せる.
この両辺の比を取れば,
となり,左辺と右辺は一見同じようだが,左辺にあるが右辺にはない.これが矛盾を起こさないためには,との比はには依らない形になっているということを結論せざるを得ない.
これで第 2 段階も証明できた.
(3) との比,すなわち,すぐ上の式で使った関数 は,実は という形式になっている. |
高熱源と低熱源の間にもう一つの熱源
があるとしよう.そしてとの間でカルノーサイクルを動かし,をもらって
を中間の熱源に捨てる.ここで次の式が成り立つだろう.
また,もう一つのカルノーサイクルを用意して,中間の熱源からをもらって,低熱源にの熱を捨てる.ここでは次の式が成り立つだろう.
ところで,この装置の全体を見れば,高熱源からをもらって,低熱源にの熱を捨てているのと同じなので次の式が成り立つ.
つまり,3 つを合わせて,
という式が成り立っていなければならないわけだが,この関係を満たすためには
の形式になっていなければならない.これで第 3 段階もクリアした.
カルノーサイクルの動作の詳細にまで踏み込まなくても,ただそれが「二つの熱源の間で働く可逆サイクルだ」という事実だけでこんなところまで言えてしまうのだから不思議なものである.
熱力学的温度
ここまで 3 つの段階を経て説明してきたことの結論は,高熱源の温度と低熱源の温度さえ決めておいてやれば,カルノーサイクルが高熱源から受け取る熱と低熱源へ捨てる熱の比は
という形に定まる,ということであった.
では
は一体,どんな形をした関数なのだろう？このあと,第 2 部の記事の中で確かめるつもりでいるが,理想気体の場合に具体的な計算をしてやると,この関数は
であるべきことが分かる.（「理想気体のカルノーサイクル」参照.）つまり,
という非常に分かりやすい関係になっているというのだ.これは便利である.しかし,理想気体ではそうなっているというだけの話だ.
ところで,ここまでの議論はカルノーサイクルに理想気体を使おうが,他の普通の気体を使おうが,全く無関係に成り立つ話だった.そこで,すぐ上の式が理想気体以外の場合でも成り立つということにしてやったらどうだろうか.言っていることが分かりにくいかも知れない.つまり温度の定義を……上の式が必ず成り立つように定義し直してやってはどうだろうか.
振り返ってもらいたい.これまで温度の定義はどうやって定めていただろうか？理想気体の場合に一定圧力の下で温度と体積が比例するというシャルルの法則を元にして,実在気体の場合にもおよそ同じ関係が成り立っているだろうと考えて使っていたのである.
しかし,上の式が絶対的に正しいと定めるような方式を使えば,理想気体以外でも,どんな圧力の下にあろうと同じように正確に使えるわけで,しかも理想気体の場合にはこれまでと何も変わるところがないのである.いかにも合理的な方法ではないか.これを提案したのはかの天才,ケルビン卿である.
この新しい温度の定義を「熱力学的温度」と呼ぶ.一方これまで何となく使ってきた,気体の体積に頼る温度の定義はそれと区別して「経験的温度」と呼ばれることがある.これからは何かと便利な熱力学的温度の方を使うことにしようではないか.
熱効率
これでようやく,「カルノーサイクルの熱効率はどれも変わらない」という先ほどの話が結論できる.
熱効率とはもらった熱の内の何パーセントを動力に変えられるかという数字であり,産業革命の頃の資本家たちが血眼で追い求めていたものだ.カルノーサイクルの場合については次のような計算で求められるだろう.
最後の等号でここまでの議論の結論を使ったのだが,何とも不思議な結果だ.温度しか出てこない.つまり,カルノーサイクルの熱効率は高熱源と低熱源の温度だけで決まり,どんな気体を選ぼうとも,どんな圧力を掛けようとも,どんな工夫をしようとも変わらないというのだ.
しかも次回ではどんな機関もカルノーサイクルの効率を決して超えられないことを示すつもりでいる.すなわち,この式が理論上の限界なのだ.
産業革命時の蒸気機関の場合,高熱源は精々 400 K,低熱源は 300 K 程度だったわけで,熱効率は 0.25 と計算できる.良くても 25 パーセント程度であって,残りは熱として無駄に捨てられてきた.実際は 10 パーセントくらいしかなかったらしい.
最近の火力発電や原子力発電といえども蒸気タービンを使っているのでこの理論上の制限からは逃れられず,高温側を 600 ℃ くらいにまで上げて効率を稼いでいる.理論上の効率の上限は 60 パーセントくらいだと計算できるが,現実には 50 パーセントに届かないくらいでとどまっている.発生した熱の半分以上が電気に変えられぬまま地球の温暖化に使われているわけだ.
修正履歴
(2004/11/22)
工事中の表記を解除.
