目的
ここでは,カルノーサイクルに理想気体を使った時に,
という関係が成り立っていることを説明しようと思う.この関係は前に「カルノーサイクル」という記事の終わりの方で「熱力学的温度」を定義するときに参考程度に使ったことがあるが,これを求めるためには断熱変化の知識が必要だったので後回しにしておいたのだった.
後回しにしておいた理由はもう一つある.カルノーサイクルから得られる重要な話は,断熱変化やカルノーサイクルの具体的な動作の内容について全く知らなくても求められるということを強調したかったのだった.
改めてカルノーサイクルの動作について,それがどれくらい実用から掛け離れたものであるかということについても確認しておくことにしよう.
カルノーサイクルの動作
前にも見たようにカルノーサイクルは次の図に表すような状態変化をたどる.
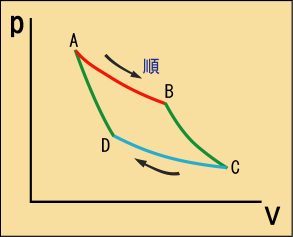
つまり,次の 4 つの過程から成る.
A → B
シリンダーの中の気体は高熱源と同じ温度になっており,高熱源に触れながら膨張する.つまり等温変化である.高熱源に触れているから膨張するわけではない.内部の気体の圧力はすでに高くなっており,いつだって膨張しようとしている.ただし勢い良く膨張させると温度が下がってしまうので,本当にゆっくりしか膨張しないように押さえつけておく必要がある.じわりと膨張しては,じわりと下がった温度を高熱源に温めてもらって一定温度を保つという理屈だ.ここで熱
をもらって外部に仕事をしたことになる.
ここで高熱源から切り離され,勢い良く断熱膨張させられる.つまり,いままで膨張しないように押さえていたつっかえ棒を急に外された感じだ.熱のやり取りがないまま外部に仕事をするので温度が下がる.この次に低熱源に触れるための準備である.
気体が低熱源と同じ温度になったので,低熱源に触れた状態で体積を減らされる過程.圧縮されることで熱が出るが,その熱は低熱源が吸い取ってくれる.仕事をされながら熱を捨てるという,動力源としては全く役に立たない部分.しかし機関を元の状態に戻すために必要な部分である.ここで捨てた熱を
とする.
再び熱源から切り離され,勢い良く圧縮される過程.外部との熱のやり取りが無いので,外部から仕事をされる分だけ熱くなる.高熱源に触れるための準備.
断熱変化の性質
ここまでは理想気体であるなしに関係ない説明だった.いよいよこれから,内部の気体が理想気体だという仮定をして具体的な計算をしてやろう.
……と思ったのだが,理想気体の断熱変化についての重要な性質を説明するのを忘れていたことに気が付いた.これがないと今回の内容はうまく説明できない.「断熱過程」のところでまとめて説明しておくべきだっただろうか.いや,今回は見せ場がないので結果的にはちょうど良い.ここでやってしまおう.
前に「断熱過程」の記事中,ポアッソンの式を求めたところの少し手前で,次のような式が出ていただろう.
この両辺を状態
から
まで積分してやると次のようになる.
右辺の細かい計算は本質ではなく面倒なので
と置いた.このまま続けよう.
指数が出てくるのも面倒なので
として書き直してやれば,
という形式にできる.つまり理想気体の時だけの話だが,断熱変化の前後の体積の比は,変化の前後の温度の関数,
の比で表せるということだ.ただ,
の形は応用するにあたってそれほど重要なわけではない.
各過程の計算
では各過程について考えて行こう.
まず A → B
ここで外部に対して行った仕事は,
と計算できる.理想気体の内部エネルギーは温度だけで決まるのだったから,等温変化で内部エネルギーの変化はないことになる.つまり,高熱源から受け取った熱は蓄えられることもなく全てこの仕事に使われていることになる.
ここで以前に求めたを使って
のような計算をしても役に立つ結果は得られない.もっと簡単な方法がある.外部との熱のやり取りがないのだから,ここで仕事をした分だけ内部エネルギーが減っているはずだ.理想気体の内部エネルギーは温度だけで決まるのだから,外部に対して行った仕事は
だと考えておけばいい.
A → B でやったのと同じように計算できるが,は外部からされた仕事と正として考えたいので,前とは符号を逆にして,
と計算できる.やはり理想気体の等温変化だから内部エネルギーの変化はない.
B → C の時と同じ理屈で,この過程で外部から行われた仕事量は,
と表せる.出入りの方向が違うだけで同じ仕事量になっている.
結論
これらの結果を一つにまとめよう.もらった熱,捨てた熱,外部に行った仕事,外部からされた仕事の収支は 1 サイクルで 0 になっていなくてはならないが,2 番目と 4 番目の仕事は打ち消しあっているので,結局残りの
という結果だけで収支は合っていることが分かる.ここから,
という関係を作ることが出来る.対数の部分がややこしいが,ここで先ほどの断熱過程での体積変化についての結果を使えば,
であることから,
が言えて,
が得られることになる.これで今回の記事の目的は果たせた.熱力学的温度の定義の根拠はここにある.いや,この事実を基準にすると都合がいいので,拡張してあらゆる場合に使うことにしましょう,と決めただけのことだが.










