ガウスの定理とは
まず,これから説明する定理についてはっきりさせておこう.ガウスの定理とは,
という関係式である.これをこれから証明する.証明するというより,理解できる程度まで解説するつもりだ.
ここで右辺のという部分が何なのか気になっているかも知れない.これは,ベクトル
の成分が
であるとしたときに,
と表せる量だ.毎回これを書くのは面倒なので
と略して書いているだけの話だ.なぜ
と書くのかと言えば,これは「divergence」の略である.ベクトルが単位体積から湧き出してくる量を意味している部分である.なぜそういう意味に解釈できるのかについてはこれから説明する.
式の意味
左辺を見ると,面積についての積分になっている.ベクトルを定義できる空間内で,閉じた面を考える.どんな形でも構わない.ある空間をすっぽり面で包んでやる.そして,その面上の微小な面積と,その面に垂直なベクトル成分をかけてやる.それを閉じた面の全面積について合計してやったときの値が左辺の意味するところである.
一方,右辺は体積についての積分になっている.先ほど考えた閉じた面の中に体積の微小な箱がぎっしり詰まっていると考える.その微小な体積
とその中で計算できる量
をかけた値を,閉じた面の内側の全ての立方体について合計してやった値が右辺の積分の意味である.
この 2 つの量が同じになるというのだ.
これは簡単にイメージできるのではないだろうか?まず,この後でちゃんと説明するのでが微小な箱からの湧き出しを意味していることを認めてもらいたい.正確には
は単位体積あたりのベクトルの湧き出し量を意味するので,微小な箱からの湧き出し量は微小体積
をかけた
で表されるべきである.
ある小さな箱の中からベクトルが湧き出して箱の表面から出て行ったとしたら,箱はぎっしりと隙間なく詰まっていると考えているので,それはすぐに隣の箱に入ってゆくことを意味する.ここで隣の箱から湧き出しがないとすれば,つまり,隣の箱からは入ったのと同じだけ外に出て行くことになる.湧き出しがないというのはそういう意味だ.ベクトルはその箱の中を素通りしたわけだ.
このようなイメージで考えると,全ての微小な箱からのベクトルの湧き出しの合計値は全体積の表面から湧き出るベクトルの合計で測られることになる.実にイメージしやすい定理だ.
なぜ divE が湧き出しを意味するのか
では最後にが本当に湧き出しを意味するのか,それはなぜなのかについて説明しておこう.これを説明すればガウスの定理についての私の解説は終わる.
先ほど,微小体積からのベクトルの湧き出しはで表されると書いた.このことが示せればいいわけだ.微小体積として,各辺が
,
,
の直方体を考える.つまり,
である.これと,
の定義式をそのまま使ってやれば次のような変形が出来る.
これで 3 つの項が出来た.まず初めの項を見てみよう.
はベクトルの
成分の
方向についての変化率を表しており,これに
をかけた量
は
方向に
だけ移動する間のベクトルの増加量を表している.
もし読者が高校生ならという記法には慣れていないことだろう.これは偏微分と呼ばれるもので,微小量
だけ変化する間に
,
方向には変化しないと見なして・・・つまり他の成分を定数と見なして微分することを意味する.
そしてベクトルの増加量にがかけられている.これは直方体の
面の面積に相当する.
つまり第 1 項は,微小な直方体の面から
方向に向かって入ったベクトルが,この直方体の中を通り抜ける間にどれだけ増加するかを表しているということだ.
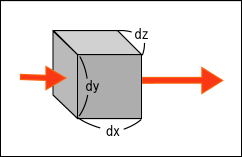
第 2 項も同様にが
方向の増加を表しており,
が
面の面積を表しているので,直方体を
方向に通り抜ける時のベクトルの増加量を表している.
もはや第 3 項についても同じ説明をする必要はないだろう.は各方向についての増加量を合計したものになっている.
マイナス方向についてもうまい具合になっている.つまり,さっきまでは軸のプラス方向へ
だけ移動した場合のベクトルの増加量についてだけ考えていたが,反対側の面から入って大きくなって出てきた場合についても
はプラスになるように出来ている.
なぜなら,軸のプラス方向からマイナス方向に向けてベクトルが入るということはベクトルの
成分がマイナスになっているということである.これが大きくなって直方体から出て来るということは
だけ進む間に
成分が減少したと見なせるわけだ.これは逆に見れば
進む間に
成分が増加したと計算できる.
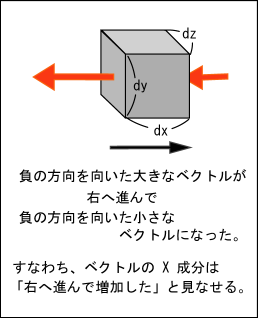
つまりというのは絵的に見たのと全く同じような意味で,ベクトルが直方体の中から湧き出してきた総量を表すようになっているのである.それで,
の意味は,と問われたら「単位体積あたりのベクトルの増加量を表す」と言えるのである.










