電磁気学：磁石の吸着力

（質問者）磁石が鉄を引き付ける力は計算できますか？

う～ん,そういえば聞いたことがありませんね.鉄と言ってもあれこれ種類がありますし,形によっても磁力線の分布が違って来ますので,難しいのではないでしょうか.

（質問者）計算は出来ないということですか？

ああ,それはいい質問の仕方です.「出来ないのか」と聞かれれば出来る方法を考えてしまうのが我々の習性です.

え～っと,ちょっと待ってくださいね.かなり理想的な条件を仮定すればできるかもしれません.

（この間0.01秒）

例えば次の図のような状況を考えてみましょう.

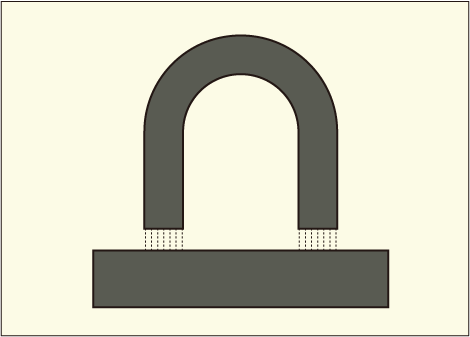
磁石が鉄と接する面が平らで,その面積をとします.磁力線は外部へは漏れておらず,接する面に対して垂直であるとします.磁力線が漏れると仮定が崩れそうなので,鉄は磁力線が内部を通るほどの十分な厚みがあると考えます.磁力線がどこにも漏れずに一周していると考えたいので,磁石の側もU字型磁石としました.

この図では磁石と鉄の間の空間の磁力線を描くために少し間をあけてありますが,あまり広げると磁力線が外側へと曲がってしまうので仮定が崩れてしまいます.隙間はとても小さいと考えてください.

平行平板コンデンサの極板間に働く引力との類推が使えそうです.あれは一方の極板に存在する電荷が作る電場を計算して,もう一方の極板上の電荷がその電場に引かれる力を求めればいいのでした.電荷の代わりに「磁荷」が存在すると仮定して,磁石と鉄の間の磁場を作っているのがその磁荷だと考えれば,磁場の大きさも力の大きさのどちらも計算できますから,最終的に磁場の強さと働く力の大きさの関係が導ける気がします.

コンデンサの極板間の引力の復習

ちょっと復習しましょう.面積の平行平板コンデンサの一方に電荷が存在するとき,面積はかなり大きくて端の方のことは無視できると仮定すると,電気力線は極板に対して垂直になります.

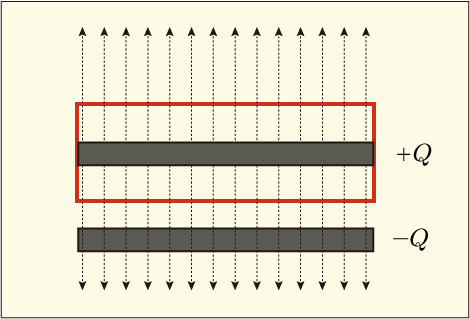
ここでガウスの法則を使います.この極板をすっぽり包む面を考えます.電気力線は上下に伸びていますから,側面の面積を考える必要はなくて,上面と下面の合計面積と電場を掛けてやれば,それは内部の電荷を誘電率で割ったものに等しくなります. こうして電場が求まります.実際にはもう一方の極板にある電荷が作る電場が重なり合わさるので 2 倍になりますが,今回は一方が作る電場にもう一方の電荷が引かれる力を知りたいのでこのように計算しました.（もしも上下の極板が作る電場が重なった状態を想定して計算すると,極板間以外の電場が 0 になるので,片面の面積と電場の積を計算することによって2倍の電場が導かれてきます.）

さて,他方の極板にも大きさの電荷が存在していて,この電場から受ける力は次のように求められます. これが極板間の引力です.復習はここまでにしましょう.

磁荷の定義

磁荷というものが存在すると仮定して,磁場はそれによって生じていると考えることにします.そのために,磁荷どうしの間に働く力は次のようなものだと仮定します. この式を次のように 2 つに分けます. 磁荷 $m_{1}$ が磁場の中に置かれたときに受ける力を表す式と,磁荷 $m_{2}$ が周囲に作り出す磁場を表す式です.

この式はマクスウェル方程式の中の一つである div B=0 という式の右辺に磁荷密度を追加して div B=g に変更したことに相当します. $B=μ_{0}H$ という関係から $div H=g/μ_{0}$ が言えて,次のようなガウスの法則が使えます. 要するに,電場と対等な関係が成り立っており,全く同じように考えることが出来ます.

磁束密度と引力の関係

磁石と鉄の間の磁力線は平行平板コンデンサと同じ状況なので,磁石の側の磁荷が作る磁場は (1) 式と同じように次のように表せます. 鉄の側にも同じ大きさの磁荷が誘起されていると仮定すると,磁石が作る磁場に引かれる力は次のような式で求められます. (7) 式を (8) 式に代入すればコンデンサの場合の (2) 式と同じ形の式になりますが,今は現実には観測できない量である磁荷を消去してやりたいので,(7) 式をと変形して (8) 式に代入してやることにします.その結果,次の式が得られます. 我々の日常では磁束密度を表す単位として「テスラ」が定着してきていますし,このを磁束密度に直しておきましょう. $B=μ_{0}H$ ですから,次のようになります. さて,注意が必要なのですが,このというのは,一方の磁石のみが作った磁場です.鉄の側に誘起された磁荷が作る磁場を合わせるとこれの 2 倍になります. このを使って書き換えれば次のようになります. 単独の磁石の表面の磁束密度を使って考えるときは (11) 式を使いますがその状況では磁力線が広がっているので正確ではなく,鉄に近付けたときの間の空間の磁束密度を使って考えるときは (13) を使いますが密着しているので磁束密度が測れないという問題があります.しかも鉄が磁石と同等にまで磁化してくれるという保証もありません.

およそ,表面積に比例し,磁束密度の 2 乗に比例するというくらいの大雑把なことは言えると思います.

（質問者）ありがとうございます！分かりやすい関係が成り立っていると知れて嬉しいです.もちろん,理想的な条件を満たすのが難しそうだということも分かりました.

どういたしまして！私もこんなことを考えたことがなくて,勉強になりました.

磁荷の定義の話

（質問者）最初の質問から外れて申し訳ないのですが,少し気になったことがあります.なぜ磁荷を導入するために H を使ったのでしょうか？最初から最後まで磁束密度 B だけを使って計算すると何か問題があったのでしょうか？

いいところを突いてきますね.そこは意外とややこしいところなので今度詳しく話しましょう.簡単に言えば,磁荷を導入するためにはを使ったほうが電場と形式を同じにできて話がスムーズになるという利点があります.もちろんを使っても説明できますが,少し面倒な議論が入ってきます.

マクスウェル方程式の上で電荷と磁荷が対等になるように表現するという点では今回の定義を採用するのは自然なことです.そのためにはを次のように定義することになったと思います. $μ_{0}$ も出てこないし,気持ちがいいですね.ところが,このままでは $F=m_{1}B$ と書くことが出来ません.両辺の次元が合っていないからです.次元の調整役として $μ_{0}$ を導入してが成り立っていると言ってしまえば問題ないわけですが,取って付けた感じで不自然に思われるでしょう.この関係が成り立っているかどうかという証明は必要ありません.この $μ_{0}$ は本当に次元の調整役に過ぎなくて,実は「この関係が成り立つように磁荷の大きさを定義します」と言っているだけのことです.しかしすぐには納得が行かずにモヤモヤするかもしれません.こういう脇道へそれるような議論を避けたかったのです.

（質問者）確かにそうですね.すぐには受け入れられない気がします.もう少し考えてからまた質問し直そうと思います.ありがとうございました.

はい.お待ちしております.