電磁気学：外積について

内積の復習

外積の前に内積を説明しておいた方が簡単かもしれない.内積は高校でも学ぶので詳しく説明する必要はないだろうと思うが外積と比較したいのだ.二つのベクトル,の内積は A・B と表現することになっていて,それぞれのベクトルの大きさを |A| , |B| と表せば, と計算してやることができる.ここでは二つのベクトルが作る角である.これはどういう意味かと言えば,一つのベクトルの大きさと,もう一つのベクトルのと同じ向きの成分の大きさを掛け合わせたものである.

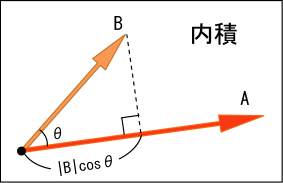
つまり,同じ向きの成分同士を掛け合わせたい時に使うのである.だから物体に力を加えた時の仕事を計算する時に「力の方向」と「力の方向に進んだ距離」をかけるのに使える.もちろん立場を入れ替えて,ベクトルの大きさと,ベクトルのと同じ向きの成分の大きさを掛け合わせたものである,と言っても同じことである.

これをベクトルの成分で計算してやることもできて,それぞれの成分を A=(x,y,z) , B=(X,Y,Z) と書けば, と表せる.説明は必要だろうか？先ほど言ったように,同じ方向の成分同士を掛け合わせるという考えをそのまま実行しただけである.とは言うものの,納得するくらいまで証明しようとするとめんどくさいんだよなぁ.

外積のイメージ

次に外積について説明するが,まず表面上の知識を伝えることから始めよう.二つのベクトル,の外積は A×B と表現することになっているが,内積の場合と違って結果はベクトルになる.だから外積のことを「ベクトル積」と呼ぶこともある.それに対して内積は「スカラー積」と呼ばれたりする.なぜベクトルになるのかは後で説明しよう.

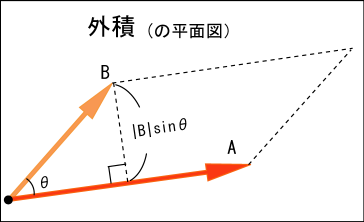
ベクトルと言うからには方向がある.それは先に書いた方のベクトルの指す方向から後に書いた方のベクトルの指す方向に向かって回転した時,その回転面に垂直な方向である.回転面に垂直な方向と言っても 2 つあるが,その内の,右ねじを回したときにねじが進むのと同じ方向がそれである.このことから,外積はかける順序によって答えが違ってくるということが分かるだろう.とを逆にするとベクトルの方向が正反対を向いてしまうわけだ.数値的にはプラスマイナスが逆転することになる. このベクトルの大きさは,それぞれのベクトルの大きさを |A| , |B| と表せば, と計算してやることができる.ただしは二つのベクトルが作る角である.

内積で cosθ を使ったから今度は sinθ を使うべきだろうというような単純な類推で外積の概念が出来上がったのではない.しかしまあ,見方によってはそうと言えなくもないか.もう少しあとで説明する.

このベクトルの大きさはちょうど二つのベクトルが作る平行四辺形の面積になっているが,それは結果であってあまり外積そのものの理解の助けにはならない.しかし知っていて損ではない.計算をするときにそういう知識が役立つことがあるのを知っている.

以上が外積の図形的イメージである.普通の教科書にはこれくらいの説明しか載ってないので外積がやたら難しいものに思えるのである.次にこのような概念を作り出すに至った思想を説明することにしよう.

外積を導入するに至った理由

外積は内積に比べて格段に複雑な気がするが,思想自体は似たようなものである.内積が「同じ方向の成分」をかけ合わせたいとの要求によって作られたのに対して,外積は「違う方向の成分」・・・すなわち互いに直角方向の成分同士をかけ合わせた値を求めたいという要求によって生まれたのである.例えば,ローレンツ力は電荷の進行方向と直角方向成分の磁場のみが意味を持つ.そのような関係は物理ではよく出てくるのだ.

外積は内積のように簡単に計算できるはずであった.二つのベクトルの大きさの積に sinθ をかけてやれば,一方のベクトルの大きさに,もう一つのベクトルのに対して直角の成分をかけ合せた大きさになる！

ところがここで問題が起こる.一つのベクトルに対して直角方向の成分と言っても,それは無数に存在するのだ！例えば方向のベクトルを考えてみよう.このベクトルに対して垂直な方向は面上のあらゆる方向である.仕方ないので方向と方向の 2 方向で代表させることにしよう.つまり,方向を向いた初めのベクトルの大きさに別のベクトルの方向成分をかけたものと,方向成分をかけたものの二つを作る事にしたのだ.もはやこの時点でこの計算結果を 1 成分で表すことはあきらめた方が良い.

この他に,軸に対して垂直な方向として軸と軸をとり,軸に対して垂直な方向として軸と軸をとってやる.こうして出来た多数の組み合わせの結果をうまく並べてスマートに表現してやる必要が出てきてしまった.外積の結果がベクトル表現になるのはこういう必然があるのである.

ここでうまいこと考えたもので,1 つのベクトルの軸の成分とそれに対して垂直なもう一方のベクトルの軸成分をかけたものを軸成分として配置することにした.こうしておけば軸と軸の一方を特別扱いすることなく対称な配置が可能になるわけだ.同じように軸と軸をかけたものは成分に配置,といった具合になる.図形的には先ほど説明した右回りの方向のベクトルを導入したことに相当する.

この考えを使ってそれぞれの成分で計算する時の式を作ってみよう.二つのベクトルの成分をそれぞれ A=(x,y,z) , B=(X,Y,Z) と表すとする.外積の結果の成分はベクトルの成分とベクトルの成分を掛け合わせたものになるので,,・・・といった具合に埋めていくと, (yZ,zX,xY) となるが,まだベクトルの軸とベクトルの軸をかけたなどを忘れている.これはどこに入れたらいいだろうか？ベクトルの立場を交換して考えればこれは軸と軸の順にかけたものであって,すでに成分に入っていると同じ意味を持つものである.よってこれも成分として入る権利がある.しかし図形的に考えて,外積ではベクトルの立場を交換すると符号が逆になるのであった.そこでこれらは, (-zY,-xZ,-yX) のように入るべきである.まとめれば次のようになる. このように計算すれば初めに図形的に考えた外積のベクトルをそれぞれの成分を使って表せるのである.

今この結果を求めた考え方が全てだというわけではない.この考え方はどうもしっくり来ないな,という人は,2 次元グラフ上に二つのベクトルを描いてやればこれが平面を表すことになるので,この一方のベクトルともう一方の直角方向成分をかけたらどうなるかというのを幾何学的に求めてやればいい.この答えが外積の成分の xY-yX となることが分かるだろう.

これくらい覚えろ！

計算がめんどくさいって？本当に覚えなくちゃいけないのかって？物理学者たるもの,これくらいはいつでも書き下せるようでなくてはならない.

しかし丸暗記するのではなくて,ほら,ちょっと規則性をつかめば簡単だろう？そのためにわざわざ分かり易いように xyz と XYZ を使って書いておいたのだ.なんて親切だろう.これ以上は過保護になるから自分で考えるように.