常微分方程式の数値解法

基本的なアイデア

ほとんどの微分方程式は綺麗に解くことはできないが,計算機を使って無理やり近似解を得ることはできると話したことがある.その解は数式として得られるのではなく,グラフとして描くことができるという意味である.ただし,グラフの形をひとつに定めるための条件,すなわち初期条件,あるいは境界条件を予め与えてやらないといけない.

今回の記事では常微分方程式について考えることにしよう.つまり描きたい関数の形は y(x) であり,見ての通り,変数は,ただ一つだけである.1 階の常微分方程式は複雑な形であっても次のような形式にまとめることができる. まずはこの形の式を満たす y(x) のグラフを描く方法を考えよう.1 階の方程式の話から始めようとしているので,この後,2 階,3 階と徐々に話が複雑になってゆくのではないかという不安を感じているかも知れない.しかし安心して欲しい.2 階以上の常微分方程式は,それが何階であっても,1 階の応用として簡単に対処できるのである.

不安を拭うために,どういうことかを簡単に伝えておこう.高階の微分方程式は 1 階の微分方程式の連立方程式に分解して表すことができる.1 階の連立微分方程式であれば,単一の 1 階微分方程式を解く時のテクニックを並行して行うことで解ける.というわけで 1 階の微分方程式を解くことはどうしても避けて通れないテクニックなのである.これでやる気が出たかな？

コンピュータにどういう手順で計算させたら効率が良いかというのは別の話なので,とりあえずは人間に分かりやすいイメージで説明してみよう.

f(x,y) の部分は何か複雑な形をしているかもしれないが,問題文によって与えられている既知関数である.だからとの具体的な値を代入してやれば一つの数値が得られるだろう.そしてその数値がに等しいというのだから,その数値というのはこれから求めたい関数 y(x) の傾きを意味するデータだということになる.そこで,ある範囲の面全体でそのデータがどんな具合になっているかをまず図示してみよう.例えば次のような形が描かれたとする.

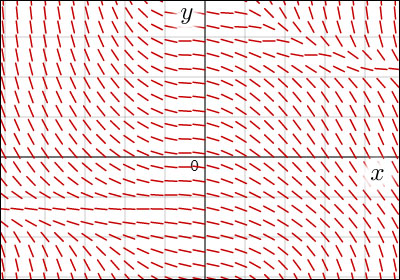
ここまで来れば,もう答は出たようなものである.横軸は,縦軸はで描いてあるので,この傾きのデータに従って線を繋いでやったものが求めるべき関数 y(x) のグラフになっている！恐ろしく簡単な話だ.

初期条件に従うようにしてこの平面上にどこか一点を決めてやり,そこからスタートして,面上の傾きデータに従って進路を描き進むのである.しかし心配なのは,本当にそれで正しい進路が描けるかどうかということだ.少しずつコースがずれて行って,それが積み重なって,本来たどるべき道とは全く違う方向へと向かってしまうことにはならないだろうか.実はそういうことは良く起こる.

それを防ぐためにはどうしたら良いだろう？上の図では傾きを計算をしている地点の間隔がかなり荒くなっているが,もっとずっと細かく計算する必要があるだろう.あまり細かくしても計算時間が掛かり過ぎて無駄なので,もう少し効率よく精度を上げる方法を工夫しないといけない.

計算の無駄と言えば,面の全体についてあらかじめ傾きデータを全て計算して保存しておく必要もなさそうだ.これは人間に状況が分かりやすいようにと思ってしたことであって,本当は必要になった地点の傾きだけ,その都度計算すれば良いということになる.

オイラー法

これで微分方程式の数値解法がだいたいどんな方針で行われるものなのかというイメージは伝わっただろう.プログラムが好きな人なら,これくらいのヒントを与えられただけで,効率の良い方法を自力で工夫して行けるかも知れない.しかしその前にもう少しだけ,先人の知恵を学んでおくのも悪くないと思う.

具体的な手順について考えて行こう.

まずはスタート地点 $(x_{0},y_{0})$ を決める.これは与えられた初期条件で決まるのである.その地点のグラフの傾きは $f(x_{0},y_{0})$ で計算できる.その点から方向に微小変位だけ移動する間に方向にはおよそ $f(x_{0},y_{0})×h$ だけ移動するはずだから,新しい地点 $(x_{1},y_{1})$ は次のように表されるだろう. この時の微小変位のことを「刻み幅」と呼ぶ.刻み幅を小さくするほど新しい地点の計算は正確になるはずだ.同様にしてさらに次の地点 $(x_{2},y_{2})$ を求めるわけだが,具体的には次のように計算することになるだろう. このようにして新たな地点の座標を次々と導くことができ,それらを線で結んだものが求めるべきグラフの形となる.これを「オイラー法」と呼ぶ.

テイラー法

しかし少しこだわりのある人ならば,このように荒っぽい直線的な近似には耐えられないに違いない.もう少し補正を加えたくなるはずだ.テイラー展開では微小変位についての補正は次の式のように表される. 先ほどのやり方では 2 項目までの近似しか使っていないことになるわけだ.しかし第 3 項までやろうとしても,そこには y'' が含まれている. y'' は直接的には値を出すことはできなさそうだ.どうしたら良いだろうか？いや,大して難しい話でもない.少し面倒だが,次のような計算をすればいいのである. 結局,次のような近似計算を使って,新たな地点を次々と求めて行けばいいということになる. ただし ∂f/∂x や ∂f/∂y がどんな関数になるかはプログラムを組む前に手計算をして具体的に求めてやらねばならない.さらに 3 次,4 次と精度を上げることも可能だが,微分計算はもっとずっと複雑になるのが想像できるだろう.というわけで,この方法が使えるのは f(x,y) がごく単純な場合に限られることになる.これを「テイラー法」と呼ぶ.

2 次のルンゲ=クッタ法（RK2）

そこで登場するのが「ルンゲ=クッタ法」と呼ばれる不思議なテクニックだ.テイラー法のような複雑な手計算をあらかじめしなくても済む.まずは騙されたと思って,次の式を受け入れてみて欲しい. この降って湧いたような近似が本当になりたっているのかどうか,変形して調べてみよう. この結果は,先ほど見たテイラー展開に 2 次まで一致している！しかし 3 次までは一致していない.「なぜこんなことが成り立っているのか？」と聞かれても,ご覧の通りだ.いや,種明かしがないこともないのだが,それを聞いてもすっきりはしないだろうと思う.それは少し後にしよう.

この近似式を y'=f(x,y) を使って書き換えれば次のようになる. この計算の途中でも近似を使ってしまっているので,本当に 2 次の精度が保証されているかどうかが疑わしくなってしまった.むしろこの結果をいきなり「受け入れてみて欲しい」と提示して,これを変形することで先ほどの「テイラー法」の近似と 2 次の精度まで一致することを確認する説明法を選んだ方が,近道かつ正確だったかも知れない.しかしこの複雑な結果をいきなり受け入れろと言われても簡単に納得できるものではないだろう.

とにかく,この結果をコンピュータで効率良く利用しようと思ったら,次のようなステップで計算するといい.使い捨ての変数とを用意してやることになる. 一番最初に一旦に $f(x_{0},y_{0})$ の値を代入しておくのは,この値を 2 番目と 3 番目の式の両方で使うからである.こうすることで $f(x_{0},y_{0})$ の値を 2 度も計算するのを避けられる. h/2 を掛けるという作業を二度に渡って計算するのも無駄なので 3 番目の式で一気にやってしまう.この計算の他に $x_{1}=x_{0}+h$ をやることで, $(x_{0},y_{0})$ から $(x_{1},y_{1})$ を導くことができるというわけだ.

上の計算の $(x_{0},y_{0})$ の部分に $(x_{1},y_{1})$ を使うことで今度は $(x_{2},y_{2})$ を導くことができる.このように同じことを繰り返すことで次々と新しい点を導いていくことができるわけだ.

実はこの方法,「ホイン法」と呼ばれることもある.ホインの綴りはちょっと変わっていて Heun である.

種明かし

ルンゲ=クッタ法にはさらに精度を高めたものがある.しかし今の説明ではなぜこんなことが成り立つのかが分からないので,どうやったらさらに精度を上げられるのかという指針もよく分からないままだろう.それで,上で使った近似式が偶然の発見以外にどうやって導かれるものなのかを理論化してみたい.

直接に考えようとすると面倒だが,コンピュータでの計算用に分解した式を参考にして表してみると分かりやすいかも知れない.先ほど使った計算手順の式に未知変数を多量に差し込んだ形のものを考えてみる. 未知変数は $R_{1},R_{2},S,T$ の 4 つである.この式の組み合わせで得られる式がテイラー展開による近似式と 2 次まで一致するための条件を考えてみよう. テイラー法の時の結果と似たような形のものが出て来た.ピッタリ一致するためには次の条件を満たしていればいい. 変数が 4 つに対して条件式は 3 つだから解は無数にあることになる.ホイン法ではその可能性の中の一つ, $R_{1}=R_{2}=1/2$ , S=T=1 を選択していたのである.

それ以外の選択肢で計算しやすいものとしては, $R_{1}=0$ , $R_{2}=1$ , S=T=1/2 というものがある.これを使う場合には次のように計算すればいい. この方法を「中点法」と呼ぶ.刻み幅だけ進むときの中点である h/2 を計算に使っているからである.こうなると使い捨ての変数やを使う積極的な理由もなさそうだが,こうやってステップに分けて書いておいた方が計算過程が見やすくて良いだろう.

4 次のルンゲ=クッタ法（RK4）

3 次のルンゲ=クッタ法というのもあるのだが,もっぱら使われるのは 4 次のルンゲ=クッタ法である.次数が増えるほど計算の手順が増えて時間が掛かるのだが,4 次まではそれに見合うほどの誤差減少の効果が得られるからだ.というわけで 4 次のルンゲ=クッタ法を紹介しておこう.

4 次のルンゲ=クッタ法にも色々とあるのだが,次のようなステップで計算できるという公式が定番である.使い捨ての変数 a,b,c,d を用意して計算することになる. この計算手順の元になっている理論式をひとまとめに書こうとすれば非常に長く複雑になることが想像できるだろう.書いたところで利点もないと思えるので書かないでおく.

これを導くためには次のような仮定をして,これがテイラー法の 4 次の項までを再現するように未知変数 R_n, S_n, T_n を決めたのだろう. 2 次のルンゲ=クッタ法との類似点が見える.もちろんここから得られる解は一通りではない.かなり面倒な計算らしいというのは人から言われなくても分かる.私もやらないでおくことにしよう.

連立微分方程式

では次に,1 階の連立微分方程式のコンピュータによる解き方を説明しておこう.1 階の連立微分方程式というのは一例を挙げれば次のようなものである. y(x) と z(x) が互いに影響し合っていてどうにも複雑そうに見える.形式的には次のようにまとめることができるだろう. しかしこれは今までに説明した方法で解けるのである. y(x) や z(x) のそれぞれの初期位置 $(x_{0},y_{0})$ や $(x_{0},z_{0})$ さえ与えてやれば,それらを始点として,次の点を計算してやれる. これはオイラー法を使ったのであって,このままでは誤差が大きいのだった.ではテイラー法を使うとどうなるかというと,素直に微分計算してやればいい.例えばの変化については次のようになる. 簡単なものだ.の変化についても同様に計算してやればいい.こうして刻み幅を進むたびに (x,y) と (x,z) の二つの新しい点を求め,それらの値を元にしてさらに次の二つの点を求める.これを繰り返せばいいのである.関数の形が複雑でなければさらに次数を上げることもできるだろう.

ではルンゲ=クッタ法を使おうとすればどうしたら良いだろうか.うまく行く理由を明快に説明するのは難しいのだが, y(x) と z(x) についての計算の各ステップを同時並行してやればいい.おおよその理屈は次の具体例を見れば察することができるだろう. ここでは 2 連立の場合についてだけ説明したが,3 連立だろうと 4 連立だろうと話は変わらない.

高階の常微分方程式

さて,いよいよ今回の話の仕上げだ.高階の微分方程式というと,例えば次のような形のものである. これは 3 階の微分方程式であるが,こういうものは次のような形式でまとめられる. ここに新しい関数 z(x) と w(x) を導入して,それぞれを z(x)=y'(x) , w(x)=y''(x) などと置いて書き換えてやれば,この式はと書けるし,この他にという関係も言えているので,3 連立の 1 階微分方程式だということになる.分かりにくいかも知れないが,これは先ほど考えた一般的な連立微分方程式の中でもかなり特殊で簡単な形になっている.一般的な 3 連立微分方程式がのような形をしていて,これらの右辺は全て問題文によって与えられる既知の関数なわけだが,今回の場合,この内の二つがという最も単純な形になっているということだからである.こういう既知関数と未知関数の違いで混乱しないように慎重にプログラムを組まないといけない.それにさえ気を付ければすでに説明したことで十分であろう.