物理数学：フーリエ級数の収束

収束について

周期で同じ形を繰り返す周期関数 f(x) が次のような「フーリエ級数」として表せるという話をした. しかしどんな周期関数の場合にでも必ずこのような等号が成り立つと言えるのかどうかについてはまだはっきりさせていなかった.

問題をもう少しだけ明確にしておこう.この右辺を第項までで中断した関数 f_m(x) というものを考える.すると $\{f_{1}(x),f_{2}(x),f_{3}(x),…\}$ と続く関数列が用意できるだろう.これが関数 f(x) に徐々に近付いてゆくかどうかを問題にしたいのである.しかしこのような表現ではまだ十分ではない.どんどん近付いては行くけれども,近付き方の幅がどんどん小さくなって行って,いつまでたってもある程度よりも差が縮まらないままだという事では困るからだ.

だから次のように言った方がいいかも知れない. |f(x)-f_m(x) | というものを考え,これが $m\to∞$ でちゃんと 0 になるという保証があるかどうか.そのような保証がある時に「この無限級数は f(x) に収束する」という表現を使うことにする.(1) 式で使っているような等号はそのような状況を意味しているとするのである.

収束の種類

ここで一旦フーリエ級数からは離れて関数列の話をしておいた方が良さそうだ.関数列 $\{f_{1}(x),f_{2}(x),…,f_m(x) ,…\}$ が収束すると言っても,その収束の仕方には色々と種類がある.その違いを紹介しておきたい.ここではイメージを話すだけにして厳密なことは数学に任せよう.

まず,関数の形の全体を見るのではなく,変数を例えば $x_{0}$ に固定したある点だけでの振る舞いを見ることにする.このときが増えるに従って, $f_m(x_{0})$ が徐々に $f(x_{0})$ の値に限りなく近付いて行ったとする.これは常に近付き続ける必要はなくて,一時的には離れるような変化をすることがあっても構わない.このような収束が $x=x_{0}$ だけでなくどの点についても起こっていると言えるならば,それを「各点収束」と呼ぶ.

これ以外の収束も考えられる.今度は最初から関数の全体の様子を見ることにする. f_m(x) と f(x) のズレの大きさがどこであってもある範囲内に収まっており,が増えるに従ってその範囲の幅が限りなく 0 に近付いて行くならば,それを「一様収束」と呼ぶ.

これら二種類の収束は似ているようで少し違う.一様収束するならば各点収束すると言えるが,各点収束していても一様収束するとは限らない.それがどんな状況であるかは後で説明しよう.

そしてさらに別の種類の収束として,「平均収束」というものがある.これは次のようにして計算できる定積分の値 I_m が,が増えるに従い,0 に限りなく近付くことである. 誤差を 2 乗したものを関数の全体で集計しているわけだ.ある意味,全体の誤差の平均を計算しているようなものである.この値が 0 に近付くなら平均収束である.

これについても,一様収束するならば平均収束すると言えるが,平均収束していても一様収束するとは限らない.このことから一様収束はとても強い条件であることが分かるだろう.

では各点収束と平均収束ではどちらが強い条件だと言えるだろうか？こちらについては何とも言えない.各点収束していても平均収束しているとは限らないし,平均収束していても各点収束しているとは限らないからである.

フーリエ級数の収束

では再びフーリエ級数の話に戻ろう.フーリエ級数の場合にはどんな時にどの種類の収束が成り立っていると言えるのだろうか？

実は, f(x) が連続で滑らかな関数であるならばそのフーリエ級数は一様収束することが証明されているのである.その証明は少々面倒で長くなるし,フーリエ級数を利用する上では必要なことではないので省略しよう.連続であるというのはグラフの線がどこでも途切れていないということで,これは隣の周期ともちゃんと線がつながっている必要がある.滑らかというのは 1 階微分した値をグラフにしたものも連続であるということである.隣の周期ともちゃんと滑らかにつながっているということを意味している.

不連続なら滑らかだとは言えないので,「滑らかな関数」と言うだけで「連続で滑らか」な関数であることを意味する.だからもう一度言い直しておこう.滑らかな関数であるならばそのフーリエ級数は一様収束する.

ではそれ以外の関数の場合には収束しないかというと,そうではない.うまく伝えるためには少し用語を追加しておく必要があるだろう.

一つの周期の中で不連続な点が有限個しかなくて,かつ無限大になるところがない関数は「区分的に連続な関数」と呼ばれる.そして関数の 1 階微分が区分的に連続な場合には「区分的に滑らかな関数」と呼ばれる.これで用語の準備はオーケーだ.

区分的に滑らかな関数であっても,連続であれば一様収束することが言える.ところどころで角張っている部分があっても,繋がってさえいれば問題なく収束するということである.

また区分的に滑らかな関数で,区分的に連続の場合には,一様収束はしないけれども不連続点を除いた範囲で各点収束することが証明されている.要するに不連続な部分があると,少しだけ調子が良くないということである.

なぜ「不連続点を除いた範囲で」という条件が必要かというと,こういうことだ.フーリエ級数は sin 関数や cos 関数の足し合わせなので,必ず連続な関数にしかならないだろう.不連続な点の近くではそのギャップをつなぐような線の形に近付くに違いない.それで,区分的に連続な関数の不連続点では,元となった関数の定義がどうであろうと,不連続のギャップのちょうど中間点の値に収束しようとするからである.

だんだんややこしく思えてきた.しかし表にすればそれほど難しいことではないのが分かるだろう.


連続	連続	一様収束
連続	区分的に連続	一様収束
区分的に連続	区分的に連続	各点収束

ところで,ここまでの話にはまだ「平均収束」が出てきていない.フーリエ級数ではどんな関数を使った場合に平均収束すると言えるのだろうか？

「滑らかな関数」と「連続で区分的に滑らかな関数」の場合は一様収束なのでもちろん平均収束もすることが言えるだろう.そして「区分的に連続で区分的に滑らかな関数」の場合にも平均収束するのである.なぜそうなるのかというイメージは後でもう少し詳しく話す必要がありそうだ.

収束しない関数の例

こうなると,ほとんどの関数でフーリエ級数が収束すると言えてしまいそうである.「至るところで不連続」であるとか,「至るところで滑らかでない」部分を含むような関数は使えないことになるが,そのような特殊な振る舞いの関数は物理では使えなくても特に困りはしないだろう.

他に収束しない関数と言えば,途中で無限大になるような関数である.例えば tan 関数や 1/x のようなものは不連続な点が有限個しかないけれども無限大になる点があるので,区分的に滑らかな関数の仲間に入れるわけにはいかない.こういうのは試しにやってみると分かるが本当に収束しなくて困るのである.

例えば f(x)=1/x が簡単そうなので少しやってみせよう.考える範囲を -L/2～L/2 に選ぶと,これは奇関数なので sin 関数だけで展開されることになる.そうした方が例としては少し楽になりそうだ. a_n =0 であり, b_n については次のように表される. この最後の Si(x) という関数は「正弦積分」として知られるもので,上の式変形から推測されるそのままの定義である. この Si(x) のグラフは次のようになる.

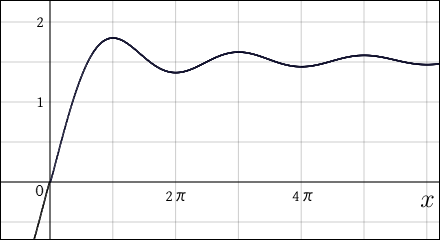
少し考えればこのグラフのようになる理由が分かるだろう.分母にあるがどんどん大きくなるのだから積分値はやがてほとんど変化しなくなる.だからが増加しようともだいたい 1.6 辺りの値をふらつくのである.

というわけで b_n の値はどこまで行っても同じような値が続くわけで,いつまでも収束しない感じが分かってもらえるだろう.途中の項までで止めたものをグラフにすると次のような感じになる.

項の数を幾ら増やしても,振動が激しくなるだけであり,元のグラフに沿う様子は見られない.その振動を均したものが元の数式の形を表しているようである.

デルタ関数のフーリエ級数

フーリエ級数が収束しない関数と言えば,デルタ関数もその一つだ.ある一点で無限大になるところがあるからである.そうとは知りつつも,どんな事になるのか試してみよう.

デルタ関数の性質を使えば次のようになるだろう. デルタ関数は 0 を含む範囲での積分に特徴があるから,計算に不都合が出ないように積分範囲を変えておいた.一周期の範囲で積分すればいいのだからこのようにしても同じことだろう.この結果を分かりやすく表せば,次のような感じである. 振幅の大きさがどれも同じである cos 関数が永久に足し合わされる形であり,収束する様子はない.収束しないから,これとデルタ関数とを等式で結ぶことは敢えてしないでおいた.しかもこの級数が表そうとしているのは単なるデルタ関数ではなく,無限大の突起が周期で繰り返すような形の関数 $Σ_{n=-∞}^{∞}δ(x-nL)$ である.

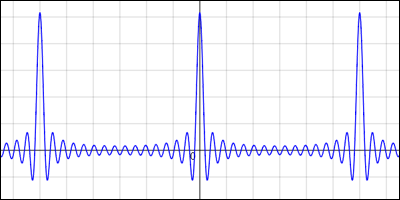
等式で表すわけにはいかないが,デルタ関数がこのような無数の波長の波の均等な足し合わせで作られているというイメージは何かの参考になるだろう.

ギブス現象

色々な形の関数をフーリエ級数の公式に当てはめて試してやると,少ない項で元の関数の形を再現してくれる場合もあれば,項の数を増やしてもなかなか形が定まらない場合もある.その違いはどんなところにあるのだろう？

当然のことだが,波長の短い波形を含ませるようにすればそれを表現する項が出現するのはずっと後回しになるだろう.ひとつの周期の前半と後半で全く違った波長にすると,前半と後半との折り合いを付けるのに少しばかり手間取る感じもあるようだが,ひどく苦手という感じでもない.滑らかでないことが問題になるだろうかと思って三角波を試してみても割りと少ない項でうまく再現してくれる.しかし途中で不連続な点がある場合,あるいは連続であってもそれに似たような形の場合は苦手なようだ.

特に苦手さが目立つのは矩形波（四角い波）を含む場合である.急激なギャップの前後でオーバーシュート（行き過ぎ）やアンダーシュート（戻りすぎ）が発生し,これは項を増やしてもなかなか解消しない.

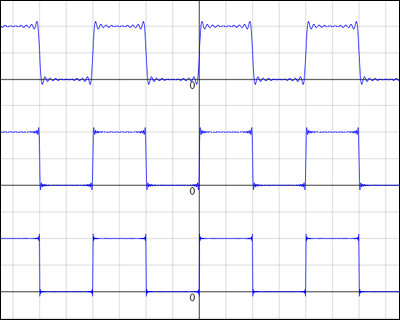
不連続点の近くに必ずつきまとうこの問題を「ギブス現象」と呼ぶ.

実はこのオーバーシュートやアンダーシュートの出っ張りは項の数をどれだけ増やそうとも消え去ることがないのである.最終的には不連続のギャップの深さに対して上下に約 9 % ずつの大きさの突起として残ることが知られている.このギブス現象が「区分的に連続」な関数の場合に一様収束しないことの原因である.参考までに書いておくと,この約 9 % というのは理論的には次のような式で求められる. このような状況であるにもかかわらず各点収束するのはなぜかというと,この余分な突起のピークは,項の数を増やせば増やすほど,幅を狭めながら不連続点の方向に向かって限りなく近付くからである.不連続点の近くのどの点であっても,このピークが過ぎ去った後では収束に向かうことになる.

平均収束する理由についてもこれで分かるだろう.突起部分は決してなくならないが,その横幅はどんどん狭くなるので誤差の 2 乗平均の計算には影響しなくなってくるからである.

ベッセルの不等式

こうして大抵の関数のフーリエ級数は平均収束することが分かった.

念のため簡単にまとめておくと,途中に無限大が含まれていたり,至るところで不連続であるような関数を除外すればいいだけである.

そういうわけだから,(2) 式の平均 2 乗誤差の計算はかなり広い範囲で収束の判断に使えそうだ.これをもう少し調べてみることにしよう.次のように変形できそうである. この第 1 項は放っておいて,第 2 項と第 3 項に (1) 式のような形を代入して計算を続けよう. f_m(x) には,(1) 式の級数を第項までで止めたものを代入する.展開するとひどく複雑になりそうだが,実はそんなに難しくはならない.前回「 $\{cosx,cos2x,cos3x,…,sinx,sin2x,sin3x,…\}$ という関数は,異なるものどうしを掛け合わせて積分した時,どの組み合わせを取ってみても 0 にしかならない」ことを確かめたのだった.ほとんどの項は消えて一部の係数だけが残るだろうことが想像できる.

途中を詳しく書いたところで複雑な印象が増すだけで役に立たないので結果だけ書くと,(3) 式の第 2 項は次のようになる. 第 3 項は次のようになる. ほとんど同じ結果であり,まとめられそうだ.第 1 項も合わせると,次のようになる. この I_m は平均収束するかどうかの指標であり,0 以上の値になっているはずである.それで次の形に書けるだろう. これは「ベッセルの不等式」と呼ばれるものである.このは代わりににしても成り立つ.平均収束する場合には等式が成り立つことも言えるだろう. こちらは「パーセバルの等式」と呼ばれている.

この式は後で重要になってくる.今回わざわざ収束について詳しく話したのはこの式を導く為であったとも言える.

今はまだこの式が複雑な感じに見えているかも知れないが,それは仕方がない.しかし視野が開けると,この式の持つ意味とイメージははっきり分かるようになるだろう.